弧光接地过电压产生的基本原理详解

图3-21(a)所示等值电路中,A相发生单相接地故障,设以u A、u B、u C代表三相电源电压,以u 1、u 2、u 3代表三相线路对地电压(也就是三相线路对地电容C 1、C 2、C 3上的电压)。

分析图3-21可知,故障点发弧后,电路中将有一电磁振荡过程。在这个振荡过程中,故障相电容C 1上的电荷通过电弧电流泄放入地,电压突降为零。两健全相电容C 2、C 3则有一个由电源线电压通过电源内电抗L S(等值电路中未画出)进行充电的高频振荡过程。

设t=t 1时刻(图3-22)故障相电源电压达最大值时故障点发弧,发弧前瞬间线路电容上的电压分别为

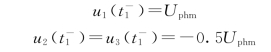
这就是振荡过程的电压起始值。其稳态值则为

回路的振荡角频率则由电路参数决定,即

若振荡频率远大于电源频率,则可认为在高频振荡过程中电源电压维持恒定,并且忽略回路损耗,则可能出现的最大过电压值为

在这个过程中,流过故障点的电流中包含两个分量,即工频分量和高频分量。由于电弧的熄灭总是在电流过零时发生,因此故障电流的熄弧时间存在两种可能性,即工频电流过零时熄弧和高频电流过零时熄弧。长期以来,多数研究者认为电弧的熄灭与重燃时间对过电压的发展过程有重要影响,因此根据不同的熄弧时间有所谓的工频熄弧理论和高频熄弧理论。按高频熄弧理论分析,得到的过电压倍数很高;按工频熄弧理论分析,得到的过电压倍数低些,似乎更接近实际情况。现场实测表明两种可能性均存在,实际上影响过电压倍数的因素很多,而且电弧过程本身有很强的随机性,因此无论哪种理论都是将具有统计性质的复杂过程作理想化的解释而已。

下面利用工频熄弧理论进行分析,以便了解弧光接地过电压的发展过程。

图3-22给出了以工频熄弧理论分析过电压发展过程的波形图。图中

图3-22　工频熄弧时弧光接地过电压的发展过程(www.xing528.com)

图3-22中,在t 1瞬间故障相燃弧后,B相、C相分别发生对地电容C 2、C 3的高频振荡的充电过程,在t 1时刻,故障电流i(t)的工频分量为零(由图3-21(b)矢量图中落后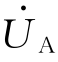 90°),t 1时刻以后的初始阶段i(t)中主要是很快衰减的高频分量。由于工频电流过零熄灭只可能发生在半个工频周期以后,即发生在t 2=t 1+时刻,所以故障电弧将持续0.01s。

t=t 2时刻第一次熄弧后又要产生过度过程。熄弧过程的电压起始值分别为

熄弧过程的电压稳态值似乎是三个相电压在时刻的瞬时值。但是由于系统中性点是绝缘的,在熄弧的过程中,各电容上的初始电荷仍保留在系统中,所以熄弧后的初始阶段必然有一个很快的电荷重新分配的过程,其结果是对地绝缘的中性点对地偏移了一个直流电位,其数值为

这个电荷重新分配过程实际上就是电容C 2、C 3通过电源电抗对C 1充电的高频振荡过程,直到三个电容上电压相等为止,因此故障电弧熄灭后,三个电容上作用有对称三相交流电压及相等的直流电压,熄弧过程的电压稳态值为

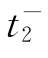由于时刻各相电压的新稳态值与时刻分别相等,因此t 2时刻故障电弧熄灭后将不会出现过渡过程。

在t 2半个周期以后即t 3=t 2+时,故障相电压达到最大值2U phm,如果这时故障点再次燃弧,u 1突降为零,电路将再次出现过渡过程。这次燃弧过程的电压起始值为

新的稳态值为

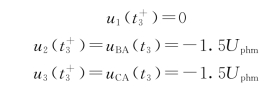
即线路电容C 2、C 3分别被电源通过电源电抗由0.5U phm充电至-1.5U phm,振荡过程中过电压最大值可达

分析可知,以后的熄弧—重燃过程将与以上第一次熄弧—重燃过程相同,过电压最大值亦相同。

显然,按工频熄弧理论分析得到的过电压倍数为3.5,并不太高,而且从波形图上可以看出过渡过程的特点:过电压的波形具有同一极性,且故障相不会产生振荡过程。