铁磁谐振：元件本身特性引起的电压变化

1.铁磁元件的非线性特性

含铁芯元件的回路,由于铁磁元件具有磁饱和现象,使它的电感值呈现非线性特性,从而导致铁磁谐振现象的一系列特征。因此,在讨论铁磁谐振现象之前,首先对铁磁元件的非线性特性作一介绍。

图3-10(a)所示铁芯线圈,其磁链Ψ及电感L随线圈中电流i变化的关系曲线如图3-10(b)所示。可见,当电流较小时,可以认为磁链Ψ与电流i成正比,反映这一关系的电感值L=Ψ/i基本保持不变。随着电流的逐渐增加,铁芯中的磁通也逐渐增加,铁芯开始饱和,磁链与电流的关系呈现非线性,电感值不再是常数,而是随着电流(磁链)的增加而减小。

上述反应电流与磁链大小比值的电感值实际上是静态电感。在过渡过程中,应该采用反应电流与磁链变化量的比值,这就是动态电感L d=dΨ/d i。对于线性电感,静态电感值与动态电感值是相同的常数;对于铁芯电感,两者是不同的,但变化的趋势是随电流的增加而减小。

不难理解,由于电感L的非线性,当交流电源作用于电感时,会发生波形畸变现象。图3-11所示为一交流正弦电动势e(t)作用在略去损耗的铁芯线圈上的等值电路及磁链Ψ、电流i随时间的变化曲线。显然,若磁链Ψ保持正弦波形,则电流i的波形将发生畸变出现尖峰,波形中出现有3次、5次、……奇次谐波。对于动态电感值L d,因为电感参数与电流或磁通的方向无关,在电流或磁链正负变化一周期内,电感参数反复变化了两次。因此得到按两倍电源频率变化的电感L d(t)的波形。

图3-11　交流电源作用在铁芯线圈上

设激磁特性用幂函数表示为

动态电感得倒数可写成

设磁链为正弦波形Ψ(t)=Ψm sinωt,代入式(3-16)并展开可得

式(3-17)表明L d(t)以电源频率的偶数倍呈现周期性的变化。据此,可将电感随时间的变化L d(t)表示为

在交流电源作用下,铁芯元件的电感值作周期性的变化,这是产生铁磁谐振的基本原因。电感值的这种变化并非外力作用引起的,而是由元件本身在交变电流或磁通作用下的特性引起的,因此铁磁谐振也称自参数谐振,以区别于参数谐振。

2.基波铁磁谐振

由于铁磁元件的非线性特性,电感值不是常数,回路没有固定的谐振频率。同样的回路中,既可能产生谐振频率等于电源频率的基波谐振,也可能产生高次谐波(如2次、3次、……)和分次谐波(如1/2次、1/3次、……)谐振。即使在基波谐振时,除基波分量外,也还有可能有高次谐波。这是铁磁谐振的重要特点。

在基波谐振时,由于其他谐波幅值很小,为了简化分析和突出基波谐振的特点,将忽略回路中其他谐波的影响。

下面分析基波谐振产生的条件及其特点。

图3-12所示为简单的串联铁磁谐振回路。设回路中只有基波电压及电流,因此可以采用复数及矢量进行分析计算。图3-13所示为电感及电容上的电压随电流变化的曲线U L(I)、U C(I),曲线上电压及电流均用有效值表示。由于C为常数,U C(I)=I/(ωC)是一条直线。铁芯电感则由于其磁饱和特性,电流较小时具有未饱和的电感值L 0,U L(I)基本上是直线;随着电流的增加,铁芯逐渐饱和,电感值下降,U L(I)不再是直线。在满足条件

(www.xing528.com)

图3-12　串联铁磁谐振回路

图3-13　串联铁磁谐振回路的特性曲线

时,在I=I K处曲线U L(I)与U C(I)有交点K,这时U L=U C,如同线性回路的谐振点。在电流I逐渐增大的过程中,电路由感性经K点后变为容性。若忽略回路电阻R,从回路元件上电压的平衡关系可以得到

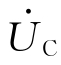因为与反相,有

ΔU(I)为回路电压降总和的绝对值,ΔU(I)与I的关系如图3-13所示。图中I=I K时,ΔU(I)=0。按照线性谐振的定义可以这样理解:如果铁芯未饱和时,回路参数满足式(3-19)的条件,则回路的自振频率低于电源频率;随着线圈中电流的增加,电感值下降,使回路自振角频率ω0上升到接近或等于电源角频率ω,满足了串联谐振的条件。总之,由于铁芯的饱和,电感值下降,使回路由非谐振状态转化为谐振状态,因此产生铁磁谐振的条件是ωL 0＞1/(ωC)。实际上,由分析可知图3-13上p(I=I K)点为不稳定工作点,回路的工作状态只能稳定在伏安特性ΔU(I)的O m段及p d段,前者称为非谐振区,后者称为谐振区。这是与线性回路的重要区别。

正是由于铁磁谐振与线性谐振产生的原因不同,因此铁磁谐振有一系列不同于线性谐振的特点,下面分别进行讨论。

根据式(3-21)电动势平衡条件,在一定的电动势E作用下,回路可能有三个平衡状态,如图3-13中a 1、a 2、a 3。但是要成为实际工作点,还必须满足稳定条件。通常用小扰动来判断平衡点的稳定性,即若有一小扰动作用于回路,使回路状态偏离平衡点之后,如果回路状态能自动返回原平衡点,则该平衡点是稳定的,能够成为回路的实际工作点;如果小扰动之后,回路状态更加偏离平衡点,则该平衡点是不稳定的,不可能成为回路的实际工作点。

对于工作点a 1,若由于某种扰动,回路电流有微小的增加,工作点由a 1点沿ΔU(I)曲线偏离到a'1,但回路电动势将小于总压降,即ΔU(I)＞E,使电流减小而返回原工作点a 1;相反,若扰动使回路电流下降,工作点由a 1偏离到a″1,ΔU(I)＜E使电流增加而返回到原工作点a 1,因此a 1点是稳定的。同理,a 3点也是稳定的。而对于a 2点,若扰动使电流稍有增加,工作点由a 2偏离至a'2,则ΔU(I)＜E,使回路电流继续增加,直到工作点偏离到稳定的平衡点a 3为止;反之,若扰动使电流稍有下降,工作点由a 2偏离至a″2,则ΔU(I)＞E,使回路电流继续减小,直到稳定的工作点a 1为止,可见a 2点不能经受任何微小的扰动,是不稳定的。

根据以上分析,在一定电源电动势E作用下,串联铁磁谐振回路存在两个可能的稳定工作点:①非谐振工作状态a 1点,回路呈电感性,回路中的电流及电感、电容上的电压都不大;②谐振工作状态a 3点,工作区域超过了特性曲线的交点K,回路呈电容性,不仅回路电流较大,电感及电容上也会出现过电压,只是由于电感元件的饱和特性,过电压的幅值会受到一定限制。

在图3-13中,如果电动势E由零逐渐增加,回路的工作点将由O点逐渐上升到m点,随后突变到n点,回路电流将由电感性突变为电容性;若电动势E继续上升,工作点将沿np变化;若此后电动势E缓慢下降,工作点将不会沿nm回到m点,而是沿np降至p点,再突降到O点,回路由电容性变成电感性。铁磁谐振回路中这种工作点的跃变现象,使回路电流相位发生180°的变化,称为相位反倾现象。

3.铁磁谐振的基本特点

(1)对于串联谐振回路,产生铁磁谐振的条件是ω0=,对一定的电感值L 0,铁磁谐振可以在很大的电容值的范围内发生。

(2)在铁磁谐振回路中,若电源电动势较小,E＜U m时,回路存在两种可能的稳定工作状态——基波的非谐振状态和谐振状态。然而,谐振状态只能激发产生,且激发消失后谐振状态大多可以自保持。若E＞U m,则只有一个基波谐振的稳定工作状态,且可以自激产生。

(3)铁磁谐振回路中的参数(电源电动势E、电容C)平滑变化时,回路工作状态可能发生突变,谐振现象可能突变式的产生或消失(称跃变现象),并且伴有相位反倾现象。例如,电源电动势逐渐上升时,回路状态由感性突变为容性,谐振现象突变式地产生。

(4)铁磁元件的非线性特性是产生铁磁谐振的根本原因,但其饱和效应本身又限制了过电压的幅值。

(5)回路损耗是阻尼和限制铁磁谐振过电压的有效措施。回路电阻增加使谐振范围缩小,过电压幅值降低,当电阻大于一定数值时,就不会激发出强烈的铁磁谐振过电压。因此在电力系统中铁磁谐振过电压多数发生在变压器空载或轻载的时候。

(6)对于铁磁谐振回路,即使是简单的串联回路,只要参数配合恰当,谐振角频率也可以是电源角频率的整数倍(高次谐波)或分数倍(分次谐波)。