对于一给定的R、L、C串联电路,若其参数![]() 、ωL,且有
、ωL,且有![]() >ωL,当有正弦交流电流流过时,由于电感与电容上的压降U L、U C反相,且其有效值U C>U L,于是电容上的压降大于电源的电动势。这就是集中参数电路中的电感—电容效应,简称电容效应。对于分布参数电路,当末端空载时,一定条件下,首端的输入阻抗为容性(如长度小于1/4波长的空载线路),计及电源内阻抗的影响(感性)时,由于电容效应不仅使线路末端电压高于首端,而且使线路首、末端电压高于电源电动势,这就是系统中的空载长线路的工频电压升高,尤其在超高压系统中这是一个重要的课题。
>ωL,当有正弦交流电流流过时,由于电感与电容上的压降U L、U C反相,且其有效值U C>U L,于是电容上的压降大于电源的电动势。这就是集中参数电路中的电感—电容效应,简称电容效应。对于分布参数电路,当末端空载时,一定条件下,首端的输入阻抗为容性(如长度小于1/4波长的空载线路),计及电源内阻抗的影响(感性)时,由于电容效应不仅使线路末端电压高于首端,而且使线路首、末端电压高于电源电动势,这就是系统中的空载长线路的工频电压升高,尤其在超高压系统中这是一个重要的课题。
当输电线路不太长时,可以用集中参数的T型或π型等值电路来代替。如图3-1(a)所示为单相线路的T型等值电路,图中R 0、L 0分别为电源的内电阻和内电感,R T、C T、L T分别为T型等值电路中的线路等值电阻、电容和电感,e(t)为电源相电势。对于空载线路,可以简化成图3-1(b)所示的R、L、C串联电路。空载线路的工频容抗X C大于感抗X L,且R一般要比X L和X C小得多,则在电源电压的作用下,回路中将流过容性电流。由于电感上压降U L与电容上的压降U C反相,且U C>U L,因此电容上的压降大于电源电动势,这就是空载线路的电容效应引起的工频电压升高,如图3-1(c)所示。其关系式如下:
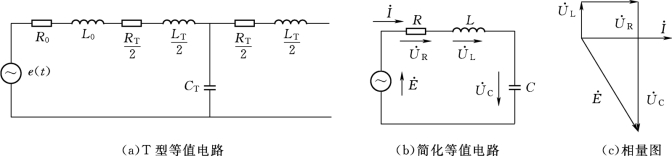
图3-1 单相输电线路的集中参数等值电路
![]()
若忽略R的作用,则
![]()
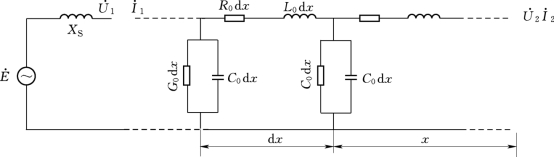
图3-2 线路分布参数链型等值电路
随着输电电压的提高和输送距离的增长,在分析空载长线的电容效应时,需要采用分布参数等值电路,如图3-2所示。由图3-2可以求得空载无损线路上距开路的末端x处的电压为式中: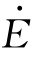 为系统电源电压;Z为线路波阻抗;X S为系统电源等值电抗;ω为电源角频率;v为光速。
为系统电源电压;Z为线路波阻抗;X S为系统电源等值电抗;ω为电源角频率;v为光速。
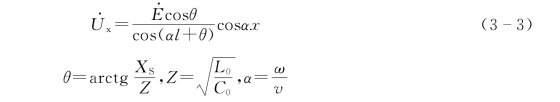

图3-3 空载无损长线电压分布
由式(3-3)可见:
(1)线路上的工频电压自首端起逐渐上升,沿线按余弦曲线分布。如图3-3所示,在线路末端电压最高。
线路末端电压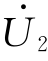 为
为
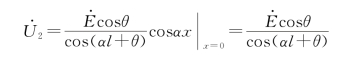
将上式代入式(3-3),得
![]()
这表明![]() 为αx的余弦函数,且在x=0(即线路末端)处达到最大。
为αx的余弦函数,且在x=0(即线路末端)处达到最大。
(2)线路末端电压升高程度与线路长度有关。线路首端电压![]() 为
为
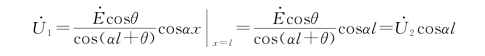 (https://www.xing528.com)
(https://www.xing528.com)
线路首端与末端的电压传递系数为

这表明线路长度越长,线路末端工频电压较首端升高得越厉害。由表3-1可知,对架空线路,α约为0.06°/km,当![]() =1500km时,αl=90°,U 2=∞。此时,线路处于谐振状态。
=1500km时,αl=90°,U 2=∞。此时,线路处于谐振状态。
表3-1 空载长线末端电压升高


图3-4 有限大电源与空载长线相连
(3)工频电压升高受电源容量的影响。图3-4所示为有限大电源与空载长线相连的单线图。当电源容量为无限大,即电源电抗X S=0时,电源电动势等于母线(即线路首端)电压![]() ,空载线路末端电压相对于电源电动势的升高可用K 12表示,即
,空载线路末端电压相对于电源电动势的升高可用K 12表示,即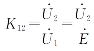 。当电源容量有限,即X S≠0时,显然空载线路末端电压对电源电动势的升高要用电源端对线路末端的电压传递系数
。当电源容量有限,即X S≠0时,显然空载线路末端电压对电源电动势的升高要用电源端对线路末端的电压传递系数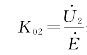 表示。
表示。
对图3-4中电源电抗及长线部分可分别视为简单的四端口网络,并用矩阵式表示为
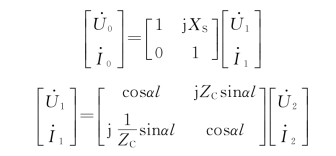
根据四端口网络链接关系式,整个电路可写成矩阵式为
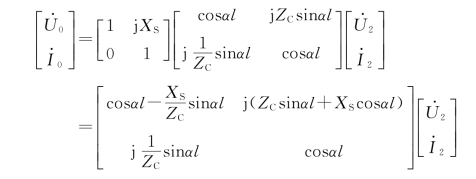
将边界条件![]() =0代入上式并化简,得
=0代入上式并化简,得
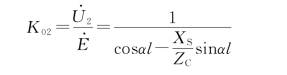
令φ=arctan![]() ,代入上式,得显然,K 02也是实数。
,代入上式,得显然,K 02也是实数。

在式(3-6)中,电源电抗X S的影响通过角度φ表示出来。分析可知,X S使线路末端电压升高得更为严重。由于αl+φ=90°时,K 02→∞,相当于αl=90°-φ。对工频线路,l<1500km,回路有可能处于谐振状态,因此电源电抗相当于增加了线路长度。实际上对于线路本身,首端与末端的电压传递系数仍由式(3-5)决定。
综上所述,电源感抗X S的存在使线路首端的电压升高,从而加剧了线路末端工频电压的升高。电源容量越小(X S越大),工频电压升高就越严重。当电源容量为无穷大时,工频电压升高为最小。因此为了估计最严重的工频电压升高,应以系统最小电源容量为依据。在单电源供电的线路中,应取最小运行方式时的X S为依据。在双端电源的线路中,线路两端的断路器必须遵循一定的操作顺序,以降低工频电压升高:线路合闸时,先合电源容量较大的一侧,后合电源容量较小的一侧;线路切除时,先切容量较小的一侧,后切容量较大的一侧。
【例3-1】 某500kV线路长300km,电源电抗X S=263.2Ω,线路参数L 0=0.9m H/km,C 0=0.01275μF/km,求线路末端开路时末端![]() 对于电源电动势
对于电源电动势![]() 的电压升高,即求
的电压升高,即求![]() 。
。
解:
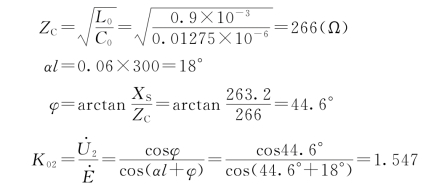
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




