有效的异常数据剔除方法

通常对某一特性指标进行多次重复测定时，常常会出现偏离平均值的一些可疑数据，对这些偏离平均值较为明显的数值是否保留还是舍弃，对平均值、标准值、标准差等的计算结果有着很大的影响，从而就很难对检测精确度和准确度给予客观的评价。可疑值的出现，多半是检测中存在过失误差造成的。只要检测人员使用合格的检测器具，按照标准规定要求细心操作，过失误差是可以避免的，从而可以大大减少检测中异常值出现的次数。如何判断可疑值，以决定是保留还是舍弃，需遵循一定的方法。对异常值进行处理，常用的处理方法有格鲁布斯检验法、Q检验法和皮尔逊检验法。

1.格鲁布斯检验法

该法用于多组测定均值一致性检验及剔除离群均值，也可用于一组测定值一致性检验及剔除离群值。具体方法如下：

（1）将一组数据由小到大顺序排列：x1，x2，…，xn-1，xn。

（2）当最小值x1异常时，计算统计量

（3）当最大值xn异常时，计算统计量

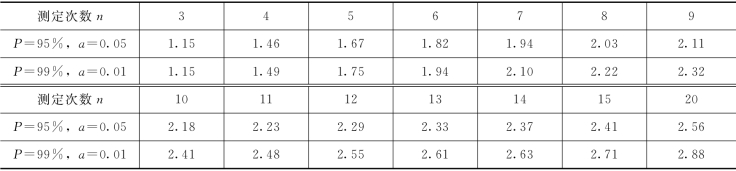
（4）将计算出的T值与从表7-1中查得的临界值T比较，如果小于该值，则x1和xn不能被舍弃；否则，可以被舍弃。

表7-1 T临界值

（5）当同一端的最大值和次大值或者最小值和次小值异常时，也可以使用此种检验方法。将数据由小到大排列：x1，x2，…，xn-1，xn；若x1、x2异常，计算总差方，计算剔除x1和x2后的总差方和，为剔除x1和x2的平均值；若xn-1，xn异常，计算总差方和，计算剔除xn-1和xn后的差方和ssn-1，n=，为剔除xn-1和xn的平均值。

（6）计算剔除异常值后的差方与总差方的比值

ss1，2/ss或者ssn-1，n/ss

若大于或等于临界值，则两个异常值保留；反之，则舍弃。

2.Q检验法

该法也用于一组测定值的一致性检验及剔除离群值。具体方法如下：

（1）将一组数字由小到大顺序排列：x1，x2，…，xn-1，xn。

（2）计算异常值与最邻近值的差值，除以全部数值的极差得出Q值。(www.xing528.com)

当x1异常时，计算统计量

当xn异常时，计算统计量

Q值越大，说明数据离群越远，将计算得到的Q值与表7-2中对应的置信度下的Q临界值数据进行对照，当计算结果大于临界值时，该异常值应当剔除，否则保留。Q检验法还可用于同侧的两个异常值的剔除，就是最大值和次大值的剔除或者最小值和次小值的剔除。

表7-2 Q临界值

3.皮尔逊检验法

当一组数据中有两个可疑值时，如果两个可疑值出现在该组数据的两端，即最大值和最小值都可疑，可以用皮尔逊检验法进行检验。

（1）将一组数据由小到大顺序排列：x1，x2，…，xn-1，xn。

（2）计算极差R与标准差s的比值

将计算所得λ和λ临界值（见表7-3）进行比较：

若λ小于或等于临界值，则x1、xn都保留。

若λ大于临界值，则x1、xn中的任何一个或两个都有可能被判为异常，此时要进一步进行检验；若x1和xn与平均值之差相近，即，两个值都作为异常值被舍弃。

若x1和xn与平均值之差相差较大，即，首先检验离x远的一个，采用上述的格鲁布斯检验法；若该值被舍弃，则对剩下的n-1个数据，重新计算，再用格鲁布斯检验法检验另一个可疑值，做出取舍决定。

表7-3 λ临界值