三相异步电动机的等效电路简介

1.折算

异步电动机定、转子之间没有电路上的联系，只有磁路上的联系，不便于实际工作的计算，为了能将转子电路与定子电路做直接的电的连接，要进行电路等效，等效要在不改变定子绕组的物理量（定子的电动势、电流及功率因数等），且转子对定子的影响不变的原则下进行，即将转子电路折算到定子侧，同时要保持折算前后f2不变，以保证磁动势平衡不变和折算前后各功率不变。为了找到异步电动机的等效电路，除了进行转子绕组的折合外，还需要进行转子频率的折算。

（1）频率折算

将频率为f2的旋转转子电路折算为与定子频率f1相同的等效静止转子电路，称为频率折算，转子静止不动时s＝1，f2＝f1。因此，只要将实际上转动的转子电路折算为静止不动的等效转子电路，便可达到频率折算的目的。实际运行的转子电流为

分子分母同除以转差率s得

上两式的电流数值仍是相等的，但是两式的物理意义不同。式（3-4）中实际转子电流的频率为f2，式（3-5）中为等效静止的转子所具有的电流，其频率为f1。前者为转子转动时的实际情况，后者为转子静止不动时的等效情况。由于频率折算前后转子电流的数值未变，所以磁动势的大小不变。同时磁动势的转速是同步转速与转子转速无关，所以式（3-5）的频率折算保证了电磁效应的不变。

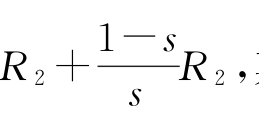由式中可看出频率折算前后转子的电磁效应不变，即转子电流的大小、相位不变，除了改变与频率有关的参数以外，只要用等效转子的电阻代替实际转子中的电阻R2即可。又可分解为其中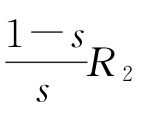为异步电动机的等效负载电阻，等效负载电阻上消耗的电功率为，这部分损耗在实际电路中并不存在，实质上是表征了异步电动机输出的机械功率。频率折算后的电路如图3-10所示。

图3-10　转子绕组频率折算后的异步电动机的定、转子电路

（2）绕组折算

进行频率折算以后，虽然已将旋转的异步电动机转子电路转化为等效的静止电路，但还不能把定、转子电路连接起来，因为两个电路的电动势还不相等。和变压器的绕组折算一样，异步电动机绕组折算也就是人为地用一个相数、每相串联匝数以及绕组系数和定子绕组相同的绕组代替相数为m2、每相串联匝数为N2以及绕组系数为Kω2而经过频率折算的转子绕组。但仍然要保证折算前后转子对定子的电磁效应不变，即转子的磁动势、转子总的视在功率、铜损及转子漏磁场储能均保持不变。转子折算值上均加“′”表示。

①电流的折算：由保持转子磁通势不变（F2′＝F2）的原则，可得

折算后的转子电流有效值为

式中　ki——电流比，ki＝(www.xing528.com)

②电动势的折算：由于定、转子磁动势在绕组折算前后都不变，故气隙中的主磁通也不变，绕组折算前后的转子电动势分别为

比较上两式得

式中　ke——称电压比，ke＝

③阻抗的折算：由折算前后转子铜损不变的原则，可得

同理，由绕组折算前后转子电路的无功功率不变可导出

以上式可见，转子电路向定子电路进行绕组折算的规律是：电流除以电流比ki，电压乘以电压比ke，阻抗乘以电压比ke与电流比ki的乘积。

注意：折算只改变相关的值大小，而不改变其相位的大小。

2.T形等效电路及其简化

根据折算前后各物理量的关系，可以作出折算后的T形等效电路，如图3-11所示。

在实际应用时，常把励磁支路移到输入端，因为励磁电流占总负载电流的比例并不很小，故励磁支路只能前移，不能略去，如图3-12所示。这样，电路就简化为单纯的并联支路，使计算更为简化，这种等效电路称为异步电动机近似的等效电路。

图3-11　三相异步电动机的T型等效电路

图3-12　异步电动机的近似等效电路