偏心距测量原理及公式示意图

1.质量和质心测量原理

质量、 质心测量的传统方法是称重法， 它是利用静力学原理设计的， 将测量仪器看作一个天平， 将弹丸放置在支架上， 通过传感器称出弹丸质量，根据力的平衡原理得出弹体的质量。 弹丸质心位置的测量可以通过测出传感器上所受的力， 再根据力矩平衡原理， 以弹丸尾部为固定端， 通过计算得出质心的位置。 如图5 -8 所示， R1 和R2 为两个测量质量的传感器， 支撑架落在这两个传感器上， 而被测弹丸则放在V 形架上。

根据力的平衡原理可得被测弹丸质量计算公式为

式中， M——被测弹丸质量， kg；

m1，m2——R1 和R2 上的称量值， kg。

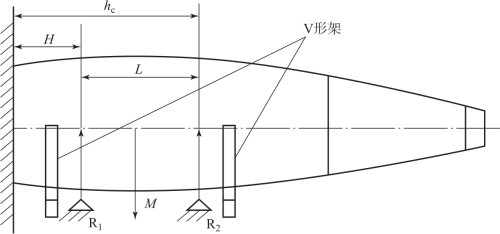
图5-8　质量、 质心测量原理示意图

根据M、 m1 和m2 这3 个质量对R1 的力矩为零， 可得质心位置计算公式为

式中， hc——质心到弹底的距离， mm；

H——弹底到Ri 的距离， mm；

L——R1到R2的距离， mm。

另一种测量质心的方法是扭摆法， 它是利用一个双张丝扭摆， 以动力学方程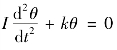为计算基础， 通过两次摆放位置的不同， 列方程得到质心的位置。 使用扭摆法测质心相对复杂一些。2.偏心测量原理

偏心的测量分为扭摆法和称重法。 扭摆法测量偏心是用双丝张紧结构扭摆作为物理变换器， 利用刚体动力学中的平衡轴原理将由弹丸偏心所产生的转动惯量变化量转换成扭摆摆动周期的变化量， 并通过电子综合测试仪进行测试， 计算并显示偏心， 其结构复杂。 偏心测量的称重法原理和测量质心的称重法原理相同， 都是根据静力学中的力矩平衡定理设计的。 如图5 -9 所示， 在被测弹丸体上划出4 等分圆周的标志线， 将支撑架落在两个测量偏心的传感器上， 质量偏心测试杆则支撑在R3 上。 测量时， 顺时针(朝R3 方向)转动被测弹丸， 使方位角指示标志对准0°、 90°、 180°、 270°标志线， 同时测量对应的为R3 上的称量值P1、 P2、 P3、 P4。

对应的4 个位置， 偏心距计算公式为

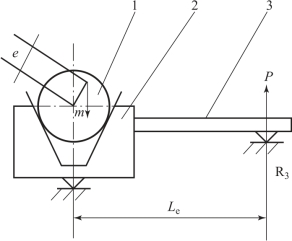
图5-9　偏心测量原理示意图

1—被测弹丸； 2—V 形架； 3—质量偏心测试杆

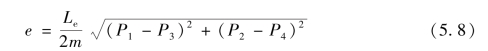
式中， e——偏心距， mm；

Le——V 形架两支撑点连线到质量偏心测试杆测头的距离， mm；

m——被测弹丸质量， kg；

P1，P2，P3，P4——被测弹丸方位角为0°、 90°、 180°、 270°时， R3 上的称量值， kg。

3.转动惯量测量原理

转动惯量是刚体转动时惯性的度量。 即在一定时间间隔内， 当主动力对转轴的力矩一定时， 刚体的转动惯量越大， 转动状态变化越小； 转动惯量越小， 转动状态变化越大。 刚体转动惯量的大小表现了刚体转动状态改变的难易程度。

刚体的转动惯量Iz 等于刚体内各质点的质量mi 与质点到轴的垂直距离ri的平方乘积之和， 即

由上式可以看出， 转动惯量不仅与质量有关， 还与质量分布有关。 对几何外形规则、 密度分布均匀的刚体， 其转动惯量可按式(5.9) 计算； 对于一些几何外形复杂， 密度分布不均匀的刚体， 它们的转动惯量不容易(甚至无法) 用公式计算， 要测得它们的转动惯量， 通常采用试验方法。 常用的方法有单线扭摆法、 三线扭摆法、 台式扭摆法等。

1) 单线扭摆法

用一根细长的金属线并借助于合适的夹具把被测弹箭悬挂起来， 使金属悬线的连线通过弹箭的质心， 并与弹轴一致(测量极转动惯量) 或与弹轴垂直(测量赤道转动惯量)。 先给弹箭一个初始转角φ0 ， 然后释放， 弹箭将在金属线的扭矩作用下做往复摆动。 若忽略空气阻力力矩， 则弹箭只受绕过质心的转轴扭转， 其摆动方程为

式中， I——总转动惯量， 包括弹箭的转动惯量Ip和夹具等的转动惯量If；

φ——扭转角度；

t——时间；

M——转动力矩；

z——弹箭系数；

f——金属线等悬挂系统的扭转弹性系数。进行适当的变换， 上式可变为

式中， T——摆动周期。

从上式可知， 转动惯量只与金属线悬挂系统的扭转弹性模数f 及摆动周期T 有关。 对于某个一定的悬挂系统， f 可认为是常数。 因此， 只要测得摆动周期T， 就可以求得转动惯量I， 再减去夹具等的转动惯量If， 便可求得弹箭的转动惯量Ip为

2) 三线扭摆法

三线扭摆系统主要由三根金属线构成。 金属线顶端固定在一个回转圆盘(固定) 上， 线间隔为120°， 回转半径为r， 下端固定在卡环(可以扭动)上， 间隔也为120°， 半径为R， 金属线长均为l。 测量时， 将弹箭夹在卡环上， 使弹箭与三线悬架的回转轴重合， 或者通过夹具使弹轴与回转轴垂直，并使弹箭质心落在回转轴上。 给回转圆盘一个初始转角φ0 ， 此时， 整个系统的质心升高h， 位能增加E1 = mgh (其中， m 是弹箭、 夹具和卡环等的总质量)。 当悬挂系统释放时， 在重力作用下它向反方向回转， 忽略摩擦阻力的影响， 当悬挂系统回转到平衡位置时， 系统的位能将全部转化为回转动能E2， 即

式中， I——整个回转系统的转动惯量；

ω——回转角速度。

与单线扭摆系统分析类似， 可得

式中， T——摆动周期；

3) 台式扭摆法

在台式扭摆装置中， 回转托盘与转轴连在一起， 安放在底座的轴承内，螺旋弹簧的一端固定在转轴上， 另一端固定在底座上。 在螺旋弹簧的扭转力矩作用下， 回转托盘随转轴在轴承座内做往复摆动。

根据转动定律， 回转系统的运动方程(忽略阻尼影响) 为

式中， J——回转部分的转动惯量；

f——螺旋弹簧的扭转系数；

φ——扭摆角。

与单线扭摆系统的方程类似， 弹箭的转动惯量为

式中， Jp——被测弹箭的转动惯量；(https://www.xing528.com)

Jf——回转装置的转动惯量。

台式扭摆法是在单线扭摆法和三线扭摆法基础上加以改进而成的， 其优点是稳定性好、 测量迅速， 而且精度高、 物体重力不参与扭摆运动、 待测物体的质心不一定通过转轴、 空气阻力影响小。

4.动不平衡量测试原理

弹丸设计上的结构不对称和生产制造中存在的壁厚差、 材料密度不均匀、装配精度达不到要求等都会造成弹丸质量分布不平衡。 弹丸的动不平衡直接影响弹丸在膛内的正确运动和对炮膛的磨损， 是形成弹丸炮口扰动的重要因素， 同时对弹丸的飞行稳定性和设计命中精度也会有很大影响。 因此精确测量弹丸的动不平衡量， 对于提高弹体质量、 提高发射准确性是必不可少的。

弹丸的动不平衡量必须在专门的动平衡机上才能测量。 动平衡机分为硬支承动平衡机和软支承动平衡机两大类， 它们是在转子旋转的状态下， 根据转子不平衡引起的支承振动(或作用于支承的振动力) 来测量不平衡。 硬支承动平衡机也称测力式动平衡机； 软支承动平衡机也称测位移式动平衡机。软支承动平衡机多用于轻小转子的平衡。 现在硬支承动平衡机以其高精度、永久性标定和结构坚固可靠的优越性在越来越大的范围取代了软支承动平衡机。

1) 硬支承动平衡机

硬支承动平衡机的支承刚度大， 转子支承系统的固有频率远高于平衡转速， 因而支承系统的振幅很小， 故转子系统的惯性力可略去不计， 且其支承系统宜用低阻尼结构。 在这种小阻尼情况下， 转子不平衡量所产生的振动频率远小于转子支承系统的固有频率， 所以支承振幅与转子不平衡量成正比，且振动的相位和不平衡量相同， 这就是现行硬支承动平衡机的工作原理， 如图5 -10 所示。

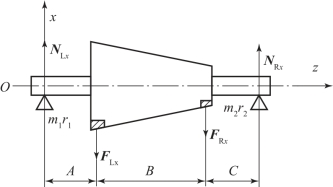
图5-10　硬支承转子及支承系统分析示意

硬支承平衡机就是根据动反力NL、 NR 来确定两校正面上离心力FL 和FR， 从而确定两校正面上的不平衡量。 由于测量是在轴承处， 而校正是在选定的两校正面上， 所以它们之间的关系是动力平衡关系； 由于转子惯性力可省略不计， 故支承反力和不平衡力是平衡的； 由于各力都是变化矢量， 故均可用复数表示， 所以可以推导出以下平衡方程：

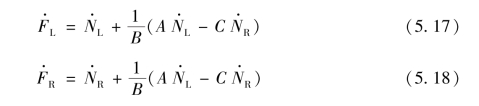
由此可见， 由不平衡量m1r1、 m2r2 产生的离心力， 仅与两轴承处的动反力NL、 NR 和轴承及校正面位置长度A、 B、 C 有关。 轴承处动反力可以通过传感器测出， 各位置尺寸可以直接测量。 最后的数据处理可以通过计算机辅助进行。

2) 软支承动平衡机

软支承动平衡机的工作原理可以简化为转子在弹性支承上以高于转子——支承系统本身固有频率的转速旋转， 在不平衡离心力的激励下而产生的受迫振动模型， 如图5 -11 所示。。 当转子以一定的转速旋转时， 在两个支承上可以分别测得振动幅值为

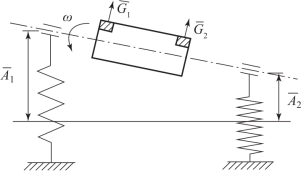
图5-11　软支承转子及支承系统分析示意

假设转子的两个校正面上分别有原始不平衡量。 根据线性系统的假设条件， 可得

式中， ——复数形式的支承影响系数。

各量的解析式为

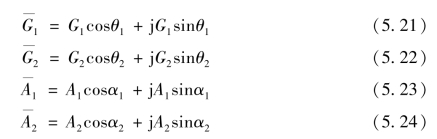
式中， θ1，θ2——不平衡量G1、 G2 相对于基准信号的相位；

α1，α2——支承振动幅值A1、 A2 相对于基准信号的相位。

分析以上式子可以看出， 只要有影响系数矩阵u4×4， 就很容易求得不平衡量的大小和相位。

3) 动平衡中不平衡量的提取算法

(1) 基于影响系数的不平衡量提取算法。

影响系数法是动平衡试验中最常用的方法， 现在大部分的解算程序都是以影响系数法作为理论基础的。

假设在某次动平衡试验中， 有m 个加重平面， n 个“测点”， 且有k(k ≤m) 个加重面的影响系数未知， 另在试验中共有h(h ≥k) 次(试) 加重。 由矩阵方程式可得出求解影响系数的通式为

式中， V0 n×h ——原始振动矩阵；

Pm×h ——h 次加重后m 个加重面所组成的加重矩阵；

Vn×h ——h 次加载后n 个测点的振动矩阵；

Kn×m ——m 个加重面n 个测点组成的影响系数矩阵。

式中， An×k，Bn×(m-k) ——将影响系数矩阵Kn×m 中与未知面相对应的未知列置于矩阵的左半部分、 与已知面相对应的已知列置于矩阵的右半部分后所得到的分解矩阵；

Ck×h，D(m-k)×h ——加重矩阵Pm×h 对应分解得到；

C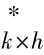 ——Ck×h 的共轭转置矩阵。

求解影响系数的通式包括影响系数求解的所有情况。 这种运用矩阵方法推导的最佳逼近意义下的影响系数计算通式， 易于实现计算机辅助计算， 可以成为目前动平衡辅助计算软件中影响系数计算的核心算法。

(2) 基于小波变换的不平衡量提取算法。

当进行动平衡测试时， 有很多干扰信号需要去除， 小波变换是其中一种重要方法。 以超微型转子动平衡机为例， 由于要提取的不平衡量信号是基波信号， 要抑制的干扰主要是高频信号， 所以最好采用正交小波基或双正交小波基， 同时还要求具有线性相位的性质。 有试验结果表明， 较好的选择是：小波变换分解算法采用滤波器长度为10 的dB5 小波基， 信号分解为4 层。 针对信号的特点， 采用强制消噪处理方法， 即把小波分解结构中的高频系数全部置0， 然后对低频信号进行重构处理。 由于电路静态工作点及温漂等的影响， 经小波处理后的重构信号通常会在正弦全波上叠加一个缓变的直流量(静态工作直流电压、 工作点漂移干扰)。 为了抑制低频干扰、 减少幅值的测量误差， 计算幅值A 的公式修改为

对不平衡量E 的估计值为

其中， E、 A1、 A2 如图5 -12 所示。

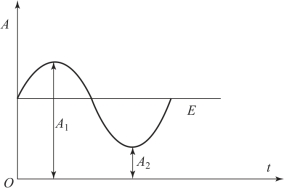
图5-12　不平衡量幅值测量

为了检测出不平衡量所对应的正弦波相角， 记录零点(即A 与E 相等)所对应的相角， 减去90° (即峰值) 所对应的相角。 实践证明， 通过记录过零点而得到峰值处的相角， 比在峰值处直接记录相角误差减小2 ～3 倍。

(3) 基于互相关的不平衡量提取算法。

基于互相关原理的不平衡量提取算法是利用互相关函数的基本特性， 将动不平衡信号与标准的同周期正弦信号进行互相关， 得到振动信号的幅值最大值和幅角， 即动不平衡量的大小和相位。 因为求互相关函数的直接算法存在着很大的缺点， 所以一般采用间接算法来求互相关函数。 其具体步骤如下：

首先， 对x(t) 与y(t) 分别并行n 次采样， 并将结果存入实数z， 其中zi =xi +jyi。 为了消除卷绕的影响， 分别对xi 与yi 的N 个数据增加零值， 成为两个2N 数据序列， 即

利用zn 的傅里叶变换zr， 可得

其中， r=0，1，2，…，m； m≤N。

用直接算法求互功率谱密度Sxy：

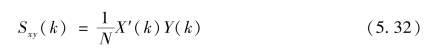
式中， X′——X 的共轭复数。

然后， 对Sxy求傅里叶逆变换， 并乘以比例因子N/(N - r) ， 取出前一半就得到Rxy。

该理论在用软件解算不平衡量及相位的测试方法和系统中得到应用。 该方法可以实现对任何形状的二维旋转部件的不平衡计算。