数字积分法又称数字微分分析法DDA(Digital Differential Analyzer)。数字积分法具有运算速度快、脉冲分配均匀,不仅可以实现一次、二次甚至高次曲线的插补,而且易于实现多坐标联动及描绘平面各种函数曲线的特点,应用比较广泛。其缺点是速度调节不便,插补精度需要采用一定措施才能满足要求。由于计算机有较强的功能和灵活性,故采用软件插补时可克服上述缺点。
根据积分法的基本原理,函数y=f(x)在t0-tn区间的积分就是该函数曲线与横坐标t在区间(t0-tn)所转成的面积,如图7-10所示。
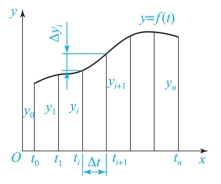
图7-10 函数y=f(x)的积分
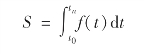
当Δt足够小时,将区间t0-tn划分为间隔为Δt的子区间,则此面积可以看作是许多小矩形面积之和,矩形的宽为Δt,高为yi。
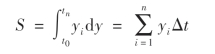
在数学运算时,若Δt取为最小的基本单位“1”,则上式可简化为

1.DDA直线插补
1)DDA直线插补原理
如图7-11所示,第Ⅰ象限直线OE,起点在原点,终点为E(xe,ye)。令υx,υy分别表示动点在x轴、y轴方向的速度,根据积分原理计算公式,在x轴、y轴方向上的微小位移增量Δx、Δy应为
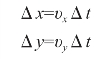
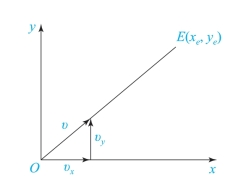
图7-11 直线插补
对于直线函数来说,υx、υy是常数,则下式成立:
![]()
式中,k——比例系数。
因此坐标轴的位移增量为
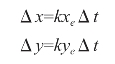
各坐标轴的位移量为
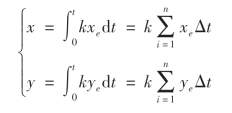
所以,动点从原点走向终点的过程,可以看作是各坐标每经过一个单位时间间隔Δt分别以增量kxe、kye同时累加的结果,据此可以作出直线插补器原理图,如图7-12所示。
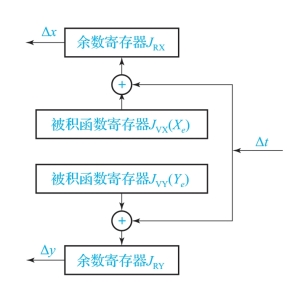
图7-12 DDA直线插补器
平面直线插补器由两个数字积分器组成,每个坐标的积分器由累加器和被积函数寄存器组成。终点坐标值存在被积函数寄存器中,Δt相当于插补控制脉冲源发出的控制信号,每发生一个插补迭代脉冲(即来一个Δt),便使被积函数kxe和kye向各自的累加器里累加一次,累加的结果有无溢出脉冲Δx(或Δy)取决于累加器的容量和kxe(或kye)的大小。
假设经过n次累加后(取Δt=1),x和y分别(或同时)到达终点(xe,ye),则下式成立:
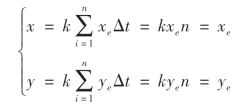
由此得到,nk=1,即n=1/k。
上式表明比例常数k和累加(迭代)次数n的关系,由于n必须是整数,所以k一定是小数。
k的选择主要考虑每次增量Δx或Δy不大于1,以保证坐标轴上每次分配进给脉冲不超过一个,也就是说,要使下式成立:
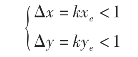
若取寄存器位数为N位,则xe及ye的最大寄存器容量为2N-1,故有
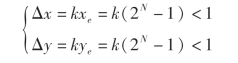
所以
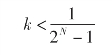
一般取
![]() (https://www.xing528.com)
(https://www.xing528.com)
可满足

因此,累加次数n为
![]()
也就是说,经过n=2N次累加,刀具将正好到达终点E。
在图7-12所示的DDA直线插补器中,被积函数寄存器JVX和JVY分别存放终点坐标xe和ye对应的余数寄存器,每当脉冲源发出一个控制信号Δt,则X积分器和Y积分器各累加一次,当累加结果超出余数寄存器容量2N时,就溢出一个脉冲Δx(或Δy),这样经过2N次累加后,每个坐标轴的输出脉冲总数就等于该坐标的被积函数值xe和ye,从而控制刀具到达终点E。
2)DDA直线插补实例
[例7-3] 设要插补第Ⅰ象限直线OE,如图7-13所示,起点在原点,终点为E(4,6),设寄存器位数为3位,试用DDA法进行插补。
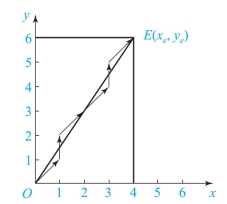
图7-13 DDA直线插补
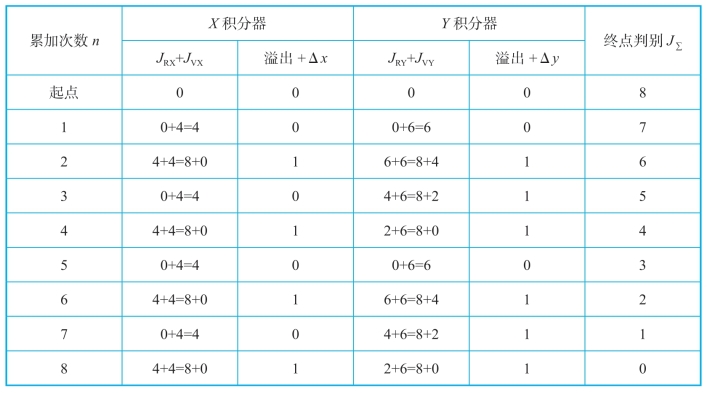
解:寄存器位数N=3,则累加次数n=23=8,插补前J∑=JRX=JRY=0,JVX=xe=4,JVY=ye=6,其插补过程如表7-3所示,插补轨迹如图7-13所示。
表7-3 DDA直线插补运算过程
2.DDA法圆弧插补
1)DDA法圆弧插补原理
以第Ⅰ象限逆圆AE为例,如图7-14所示,圆心在坐标原点O,起点为A(xa,ya),终点为E(xe,ye),圆弧半径为R,进给速度为υ,在两坐标轴上的速度分量为υx和υy,动点为N(xi,yi),则根据图中几何关系,有以下关系式:
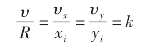
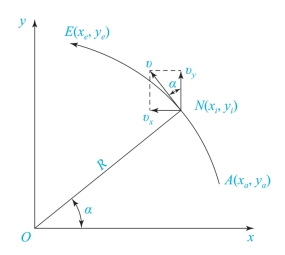
图7-14 DDA逆圆弧插补
在时间Δt内,在x、y轴上的位移增量分别为
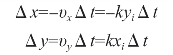
式中,由于第Ⅰ象限逆圆对应x轴坐标值逐渐减小,所以Δx表达式中取负号,也就是说,υx和υy均取绝对值,不带符号运算。
与DDA直线插补相类似,也可以用两个积分器来实现圆弧插补,如图7-15所示。但必须注意它与直线插补器相比有很大的区别。
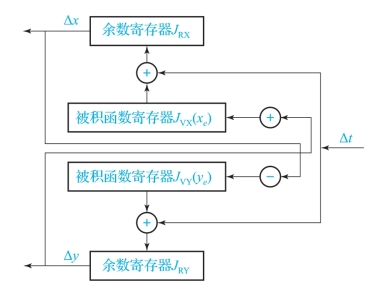
图7-15 第Ⅰ象限DDA圆弧插补器
(1)被积函数寄存器JVX、JVY的内容不同。
圆弧插补时JVX对应y轴坐标,JVY对应x轴坐标。
(2)被积函数寄存器中存放的数据形式不相同。
直线插补时,JVX和JVY分别存放对应终点坐标值,对于给定的直线来说是一个常数;而在圆弧插补时,JVX和JVY中存放的是动点坐标,属于一个变量,也就是说随着插补过程的进行,要及时修正JVX和JVY中的数据内容。例如,对于图7-14所示的DDA逆圆弧插补来说,在插补开始时,JVX和JVY中分别存放起点坐标值,在插补过程中,每当y轴溢出一个脉冲(Δy),JVX对应“+1”;反之,每当x轴溢出一个脉冲(-Δx),JVY对应“-1”。至于何时取“+1”或“-1”,取决于动点N所在象限和圆弧的走向。图中的“+”和“-”就表示动点坐标的“+1”修正和“-1”修正关系。
(3)DDA圆弧插补终点判别须对x、y两个坐标轴同时进行,这时可利用两个终点计数器中J∑x=|xe-xa|和J∑y=|ye-ya|来实现。当x或y坐标轴每输出一个脉冲时,则将相应终点计数器减1,当减到0时,则说明该坐标轴已到达终点,并停止该坐标的累加运算。只有当两个终点计数器均减到0时,才结束整个圆弧插补过程。
2)DDA法圆弧插补举例
[例7-4] 设有第Ⅰ象限逆圆弧AE,起点为A(4,0)、终点为E(0,4),且寄存器位数N=3。试用DDA法对此进行插补。
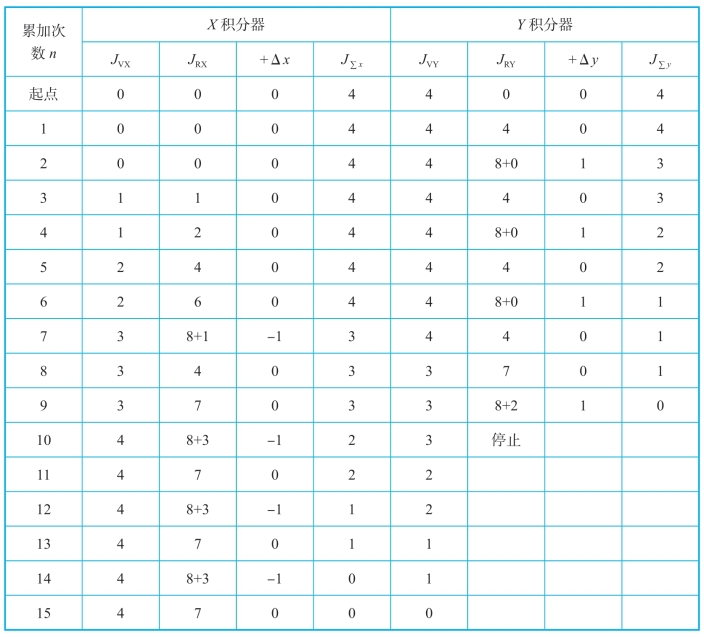
解:插补开始时,被积函数初值分别为:JVX=ya=0,JVY=xa=4。寄存器位数N=3,终点判别寄存器J∑x=|xe-xa|=4,J∑y=|ye-ya|=4。其插补过程如表7-4所示,插补轨迹如图7-16所示。
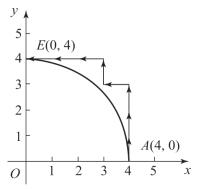
图7-16 DDA逆圆弧插补
表7-4 DDA圆弧插补运算过程
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




