解析插补法与线性插补法的区别优缺点

1．逐点比较法插补原理

逐点比较法又称为区域判别法或醉步式近似法，它的基本原理是：逐点比较刀具与编程轮廓之间的相对位置，并根据比较结果决定下一步的进给方向，使刀具向减少偏差的方向移动，而且每次只有一个方向移动，周而复始，直至全部结束，从而获得一个非常接近于编程轮廓的轨迹。

利用逐点比较法进行插补，每进一步都要经过四个工作步骤，如图7-1所示。

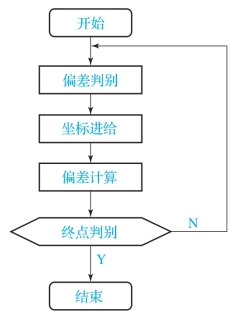
图7-1　逐点比较法工作循环

1）偏差判别

根据偏差值的符号，判别当前刀具相对于零件轮廓的位置偏差，以此决定刀具移动的方向。

2）坐标进给

根据偏差判别的结果，控制相应的坐标轴进给一步，使刀具向零件轮廓靠拢。

3）偏差计算

刀具进给一步后，针对刀具新的位置计算新的偏差值，为下一次判别做准备。

4）终点判别

刀具进给一步后，需要判别刀具是否已经到达零件轮廓的终点。如果已经到达终点，则停止插补过程；否则返回到第1）步，重复上述四个工作步骤。

逐点比较法可以实现直线插补，也可以实现圆弧插补。这种插补法的特点是运算直观，插补误差小于一个脉冲当量，输出脉冲均匀，速度变化小，调节方便。

2．直线插补

1）偏差计算

设被加工直线OE位于xOy平面的第一象限内，起点为坐标原点，终点为E（xe，ye），如图7-2所示。

图7-2　直线方程

直线方程为

改写为

直线插补时，所在位置可能有三种情况：位于直线的上方（如A点），位于直线的下方（如C点），在直线上（如B点）。

对于位于直线上方的点A（xa，ya），则有

对于位于直线下方的点C（xc，yc），则有

对于位于直线上的点B（xb，yb），则有

因此可以取偏差判别函数F为

用此式来判别刀具和直线的偏差。

综合以上三种情况，偏差判别函数F与刀具位置有以下关系：

F=0，刀具在直线上；

F＞0，刀具在直线上方；

F＜0，刀具在直线下方。

为了便于计算机计算，下面将F的计算简化如下：

设在第一象限中的点（xi，yi）的F值为Fi，则

若沿+x方向走一步，则

因此，新的偏差判别函数为

若沿+y方向走一步，则

则新的偏差判别函数为

2）坐标进给

第一象限直线偏差判别函数与进给方向的关系如下：

F≥0，沿+x方向走一步，F←F-ye；

F＜0，沿+y方向走一步，F←F+xe。

3）终点判别

每进给一步后，都要进行一次终点判别，以确定是否到达直线终点。

直线插补的终点判别可采用两种方法：

（1）把每个程序段中的总步数求出来，即n=|xe|+|ye|，每走一步则n-1，直到n=0时为止；

（2）每走一步判断xi-xe≥0，且yi-ye≥0是否成立，如果成立，则插补结束。

4）直线插补软件流程图

逐点比较法第一象限直线插补软件流程如图7-3所示。

(www.xing528.com)

图7-3　第一象限直线插补软件流程

5）直线插补举例

［例7-1］　设欲加工第一象限直线OE，终点坐标为xe=3，ye=5，用逐点比较法加工直线OE。

开始时刀具在直线起点，即在直线上，故F0=0，表7-1列出了直线插补运算过程，插补轨迹如图7-4所示。

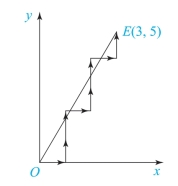
图7-4　直线插补轨迹

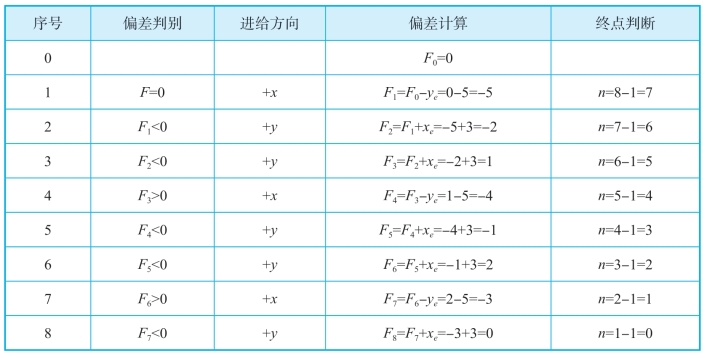
表7-1　直线插补运算过程

3．圆弧插补

在圆弧加工过程中，要描述刀具与编程圆弧之间的相对位置，可用动点到圆心的距离大小来反映。

1）偏差计算

以第一象限逆圆为例推导偏差计算公式。设圆弧起点为A（x0，y0），终点坐标为B（xe，ye），以圆心为坐标原点，如图7-5所示。

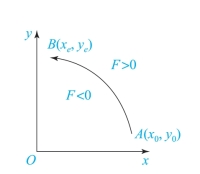
图7-5　第一象限逆圆弧

设圆上任意一点为（xi，yi），则圆的方程为

取偏差函数为

若F=0，则动点在圆弧上；

若F＞0，则动点在圆弧外侧；

若F＜0，则动点在圆弧内侧。

设在第一象限中的点（xi，yi）的F值为Fi，则

若动点沿-x方向走一步，则

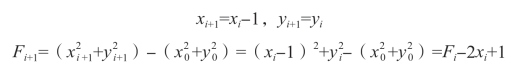
若动点沿+y方向走一步，则

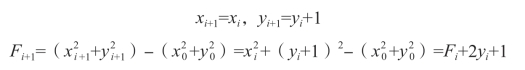
2）坐标进给

第一象限逆圆偏差判别函数F与进给方向的关系如下：

F≥0，沿-x方向走一步，

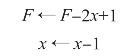
F＜0，沿+y方向走一步，

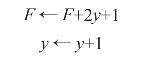
3）终点判别

圆弧插补时每进给一步也要进行一次终点判别，其方法与直线插补相同。

4）圆弧插补软件流程图

逐点比较法第一象限逆圆插补软件流程如图7-6所示。

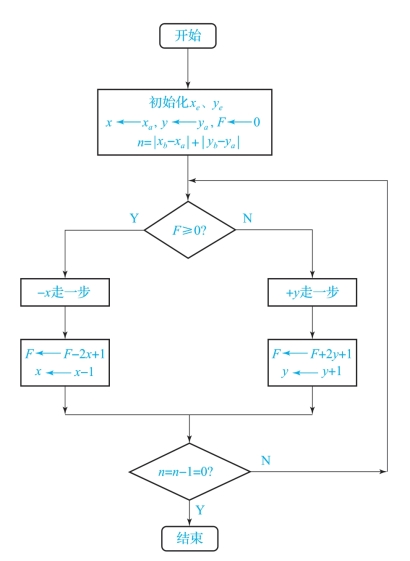
图7-6　逐点比较法第一象限逆圆软件流程

5）圆弧插补举例

［例7-2］　设AB为第一象限逆圆弧，起点为A（5，0），终点为B（0，5），用逐点比较法加工圆弧AB。

开始加工时刀具在起点，即在圆弧上，F0=0。加工运算过程见表7-2，插补轨迹如图7-7所示。

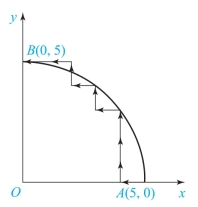
图7-7　圆弧插补轨迹

4．插补象限和圆弧走向处理

以上介绍的直线插补和圆弧插补均是针对第Ⅰ象限直线和第Ⅰ象限逆圆弧这种特定情况进行的。但实际上，任何机床都必须具备处理不同象限、不同走向轮廓曲线的能力，而此时其插补计算公式和脉冲进给方向都是不同的，一般可做如下处理。

表7-2　圆弧插补运算过程

1）四象限直线插补

现将第Ⅰ、Ⅱ、Ⅲ、Ⅳ象限内的直线分别记为L1、L2、L3、L4；对于起点不在原点的直线可以采用坐标平移的方法使其起点在原点。仿照第Ⅰ象限直线插补的情况，推出4个象限直线插补的进给方向，如图7-8所示。

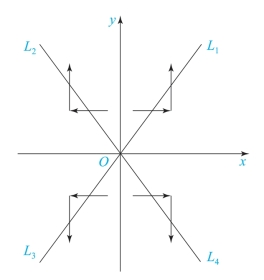
图7-8　四象限直线插补进给方向

2）四象限圆弧插补

对于圆弧，用“S”表示顺圆、“N”表示逆圆，结合象限的区别可获得8种圆弧形式，4个象限顺圆弧可表示为SR1、SR2、SR3、SR4；4个象限逆圆弧可表示为NR1、NR2、NR3、NR4。对于圆心不在原点的圆弧，同样可以采用坐标平移的方法使其圆心在原点。仿照第Ⅰ象限逆圆弧插补的情况，推出4个象限圆弧插补的进给方向，如图7-9所示。

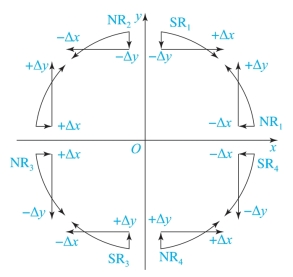
图7-9　四象限圆弧插补进给方向

此外，对于跨越几个象限的圆弧插补，还要考虑过象限问题。此时，可根据圆弧过象限时必有一个坐标值为零，以及圆弧过象限时圆弧走向不变（即逆圆弧过象限的转换顺序是：NR1→NR2→NR3→NR4→NR1→…；顺圆弧过象限的转换顺序是：SR1→SR2→SR3→SR4→SR1→…）的原则，调用不同的插补算法。在终点判别方法上，需要采用终点坐标法，判别xe-xi=0和ye-yi=0成立与否，若成立，则停止插补，否则继续。