误差评定影响齿轮传递运动准确性的方法

1.齿圈径向圆跳动误差ΔF_r（公差F_r）

齿圈径向圆跳动误差ΔF_r是指在齿轮一转中测头在齿槽内或轮齿上的齿高中部与齿廓双面接触，测头相对于齿轮轴线的最大变动量，如图8-1所示。

ΔF_r主要反映由于齿坯偏心造成的齿轮径向的周期误差，径向误差又导致了齿圈径向圆跳动的产生，如图8-2所示。

图8-1 齿圈径向圆跳动误差ΔF_r

图8-2 齿圈径向圆跳动

规定齿圈径向圆跳动的公差F_r，是对齿圈径向圆跳动误差ΔF_r的限制。

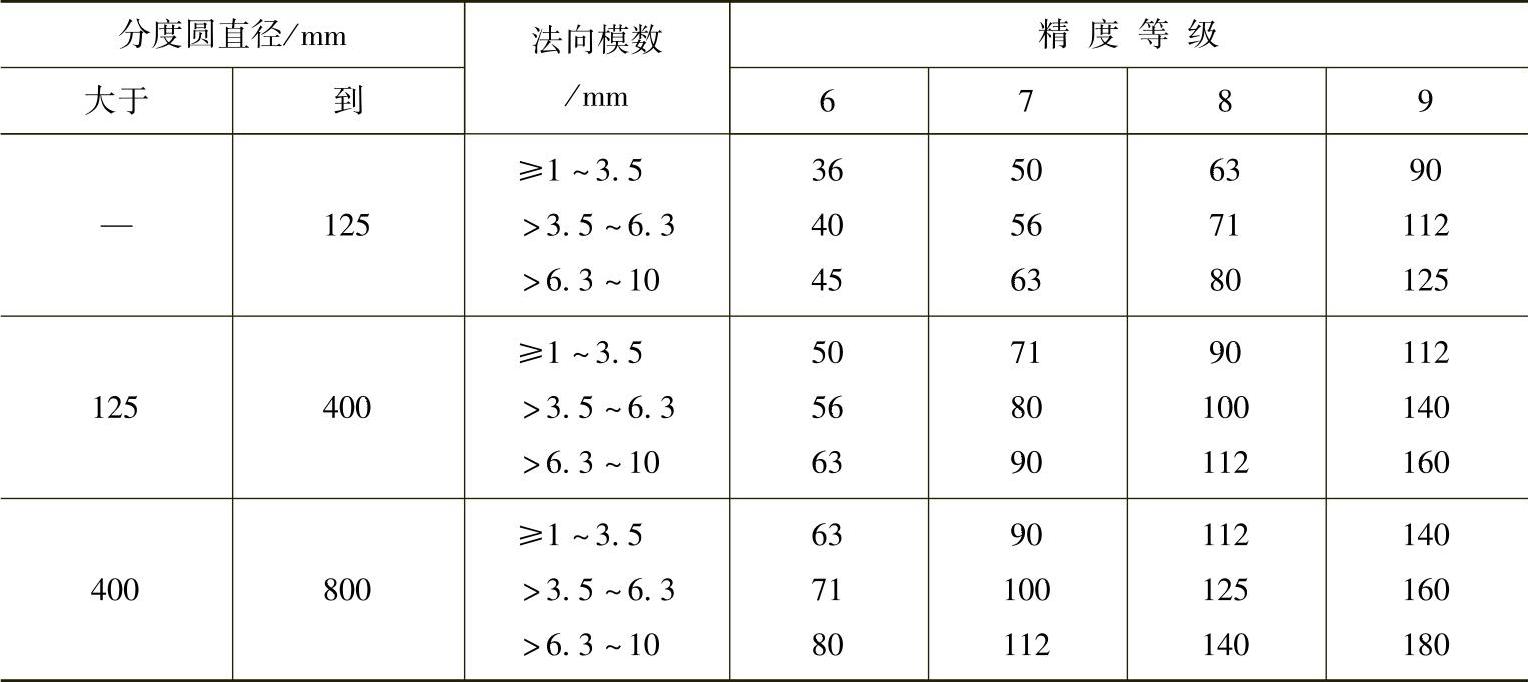
齿圈径向圆跳动误差ΔF_r的合格条件是：ΔF_r≤F_r，具体要求数值见表8-1。

表8-1 齿圈径向圆跳动公差F_r值（摘自GB/T 10095—2008） （单位：μm）

（续）

喷润滑油时：ν＜10m/s，j_bnmin=0.01mm；

10m/s＜ν＜25m/s，j_bnmin=0.02mm；

25m/s＜ν＜60m/s，j_bnmin=0.03mm；

ν＜60m/s，j_bnmin=0.03～0.05mm。

2.径向综合误差ΔF_i″（公差F_i″）

ΔF_i″是指被测齿轮与理想精确的测量齿轮双面啮合时，在被测齿轮一转中双啮中心距的最大变动量，如图8-3所示。

图8-3 径向综合误差曲线

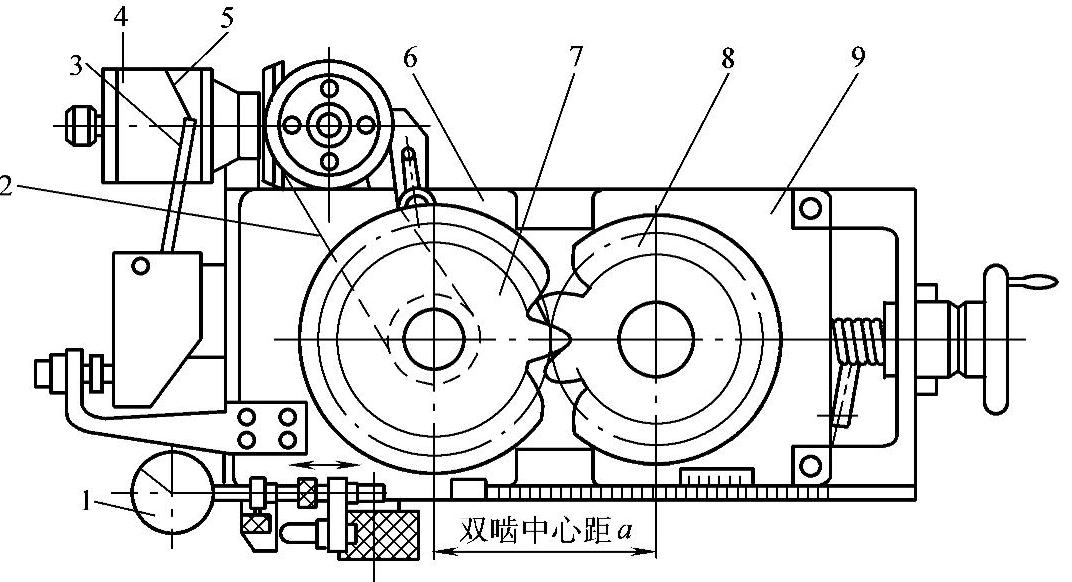
图8-4 双面啮合仪测量ΔF_i″

1—指示表 2—传动带 3—划针 4—记录纸 5—误差曲线 6—浮动拖板 7—测量齿轮 8—被测齿轮 9—固定拖板

ΔF_i″可采用双面啮合仪测量，如图8-4所示，被测齿轮安装在固定滑座上，标准齿轮装在浮动滑座上，由弹簧顶紧使两齿轮紧密双面啮合。齿轮啮合转动时，由于被测齿轮的径向周期误差推动标准齿轮及浮动滑座，使中心距变动，通过指示表测出最大和最小中心距变动数值，即为径向综合公差ΔF_i″。由指示表读出或自动记录仪画出误差曲线，其最大幅值即为ΔF_i″。F_i″的合格条件是：ΔF_i″≤F_i″。具体数值见表8-2。

表8-2 径向综合公差F_i″值（摘自GB/T 10095—2008） （单位：μm）

3.公法线长度变动误差ΔF_w（公差F_w）

ΔF_w是指在齿轮一圈范围内实际公法线长度的最大值与最小值之差（见图8-5）。

公法线长度是指跨n个齿的异侧齿廓间的公共法线长度，从图8-6可看出公法线长度变动误差为

ΔF_w=（n-1）P_b+s_j(www.xing528.com)

式中 n——跨齿数；

P_b——基节；

s_j——基圆上的齿厚。

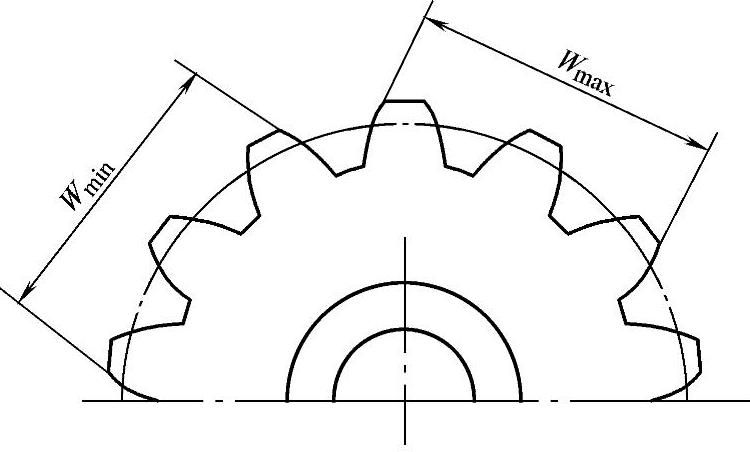
图8-5 公法线长度变动误差ΔF_w

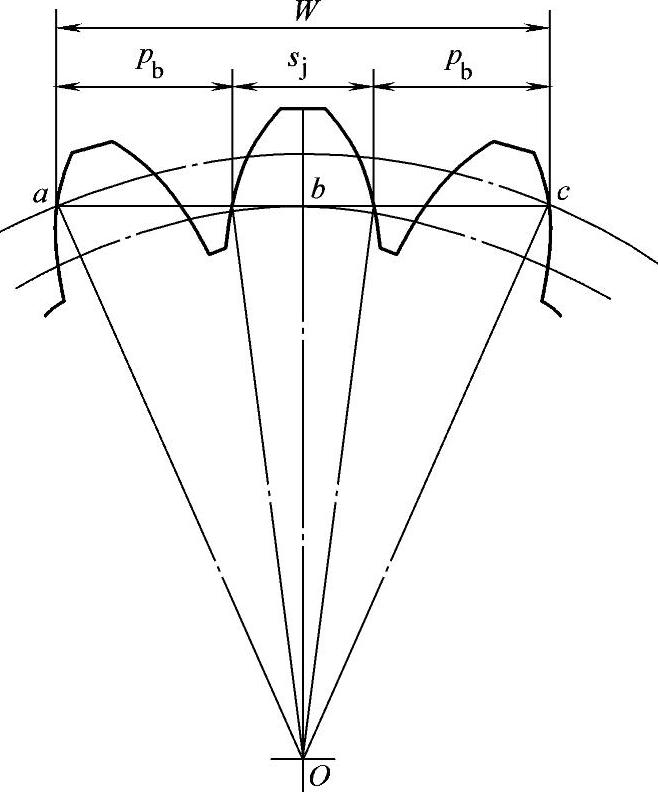
图8-6 公法线长度

由于蜗轮偏心使齿坯转速不均匀，引起左右齿面切削不均匀，使公法线长度变动误差在齿轮一圈中呈周期性变化。因此ΔF_w主要反映由蜗轮偏心而造成的齿轮切向长周期误差。

测量公法线长度变动误差最常用的量具是公法线指示卡规，如图8-7所示，一般在齿圈上测量4、5个方位取ΔF_w=W_max-W_min。

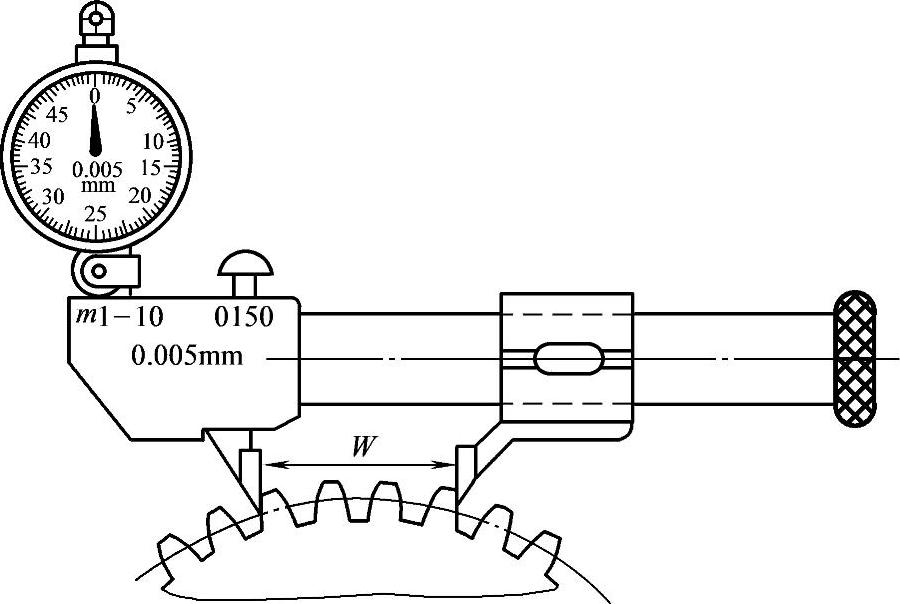
图8-7 公法线指示卡规

测量公法线长度变动误差也可用公法线千分尺，如图8-8所示，其分度值为0.01mm，用于一般精度齿轮的公法线长度变动误差的测量。

图8-8 公法线千分尺

公法线长度变动公差F_w是对公法线长度变动误差ΔF_w的限制。ΔF_w的合格条件为ΔF_w≤F_w。

表8-3 公法线长度变动公差F_w值（摘自GB/T 10095—2008） （单位：μm）

4.切向综合误差ΔF_i′（公差F_i′）

切向综合误差是指被测齿轮与理想精确的测量齿轮（允许用齿条、蜗杆等测量）作单面啮合时，在被测齿轮一周内，实际转角与公称转角之差的总幅值，以分度圆弧长计值。

若切向综合误差ΔF_i′不大于切向综合公差ΔF_i′，即ΔF′≤F_i′。则齿轮传递运动准确性满足要求。

切向综合误差是用单面啮合综合检查仪测量的，如图8-9a所示。图8-9a是双圆盘摩擦式单面啮合仪测量原理示意图。被测齿轮1与作基准的理想精确测量齿轮2在公称中心距下形成单面啮合齿轮副的传动。直径分别等于齿轮1和齿轮2分度圆直径的精密摩擦盘3和4作纯滚动形成标准传动。若被测齿轮1没有误差，则其转轴5与摩擦盘4同步回转，传感器6无信号输出。若被测齿轮1有误差，则转轴5与摩擦盘不同步，两者产生的相对转角误差由传感器6经放大器传至记录仪，便可画出一条光滑的、连续的齿轮转角误差曲线（见图8-9b）。该曲线称为切向综合误差曲线，ΔF_i′是这条曲线的最大幅值。

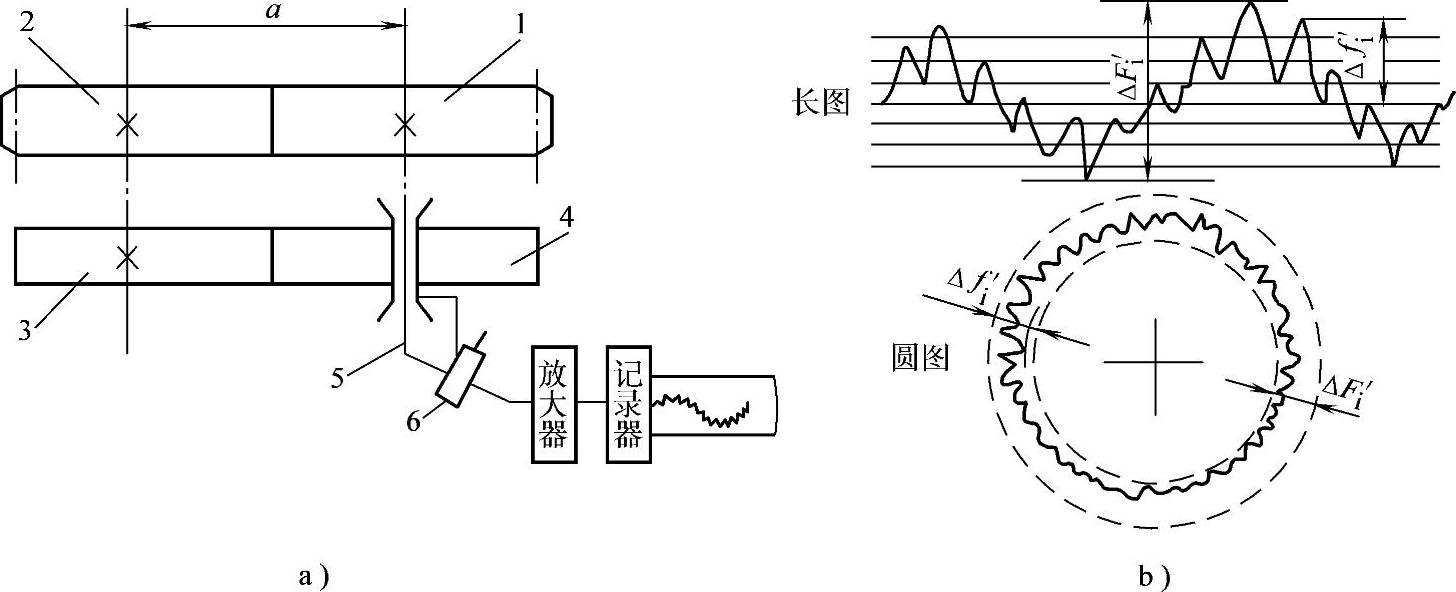
图8-9 单面啮合综合测量

a）双圆盘摩擦式单面啮合仪测量原理 b）切向综合误差曲线

1—被测齿轮 2—测量齿轮 3、4—精密摩擦盘 5—转轴 6—传感器

5.齿距累积误差ΔF_p（公差F_p）、k个齿距累积误差ΔF_pk（公差F_pk）（见表8-4）

齿距累积误差是指在分度圆上（允许在齿高中部测量），任意两个同侧齿面的实际弧长与公称弧长之差的最大绝对值。k个齿距的累积误差是指在分度圆上，k个齿距的实际弧长与公称弧长之差的最大绝对值，如图8-10所示。使用齿距仪测量ΔF_p，如图8-11所示。

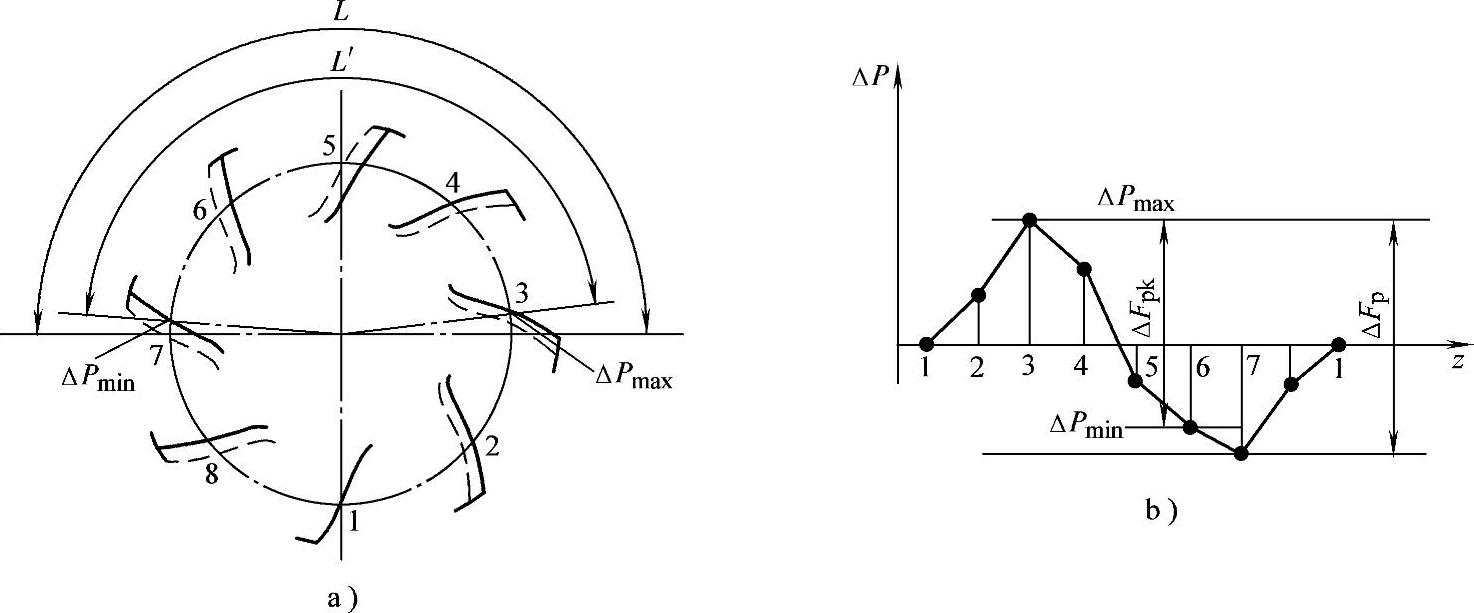
图8-10 齿距累积误差

齿距累积误差的合格条件为：ΔF_p≤F_p