有效数字的定义及处理原则

1.有效数字

在测量过程中，由于各种因素的影响，使测量结果总是含有误差，这种含有误差的数值称近似值。近似值包括经测量所得的测得值、各种计算的计算结果和各种数学常量，如π=3.14159265…，在使用时一般取π=3.1416，该常量中包含有误差。

对测量结果的数字位数的取法是测量过程中经常遇到的问题。测量结果的有效位数不宜过多，过多易使人误认为测量精度高；也不宜过少，太少易使精度受损失。为此要正确确定测量结果的有效数字位数。有效数字位数是根据测量误差的大小而定的。

例如用分度值为1mm的钢直尺测量一个物体的长度为123.4mm，其中123mm是从钢直尺上直接读出来的，是精确的；而0.4mm是用眼睛估计出来的，是不可靠的或存疑的。实测数据都应该这样表达出来，即最后一个数字是存疑数字，误差就发生在这位数字上。

用测量范围为0～25mm、分度值为0.01mm、极限误差为±0.004mm的千分尺测量轴径，测得值为20.015mm，该轴的真值在（20.015-0.004）～（20.015+0.004）mm范围内，可见测得值中小数点后第一位和第二位数是可靠的，而第三位数是不可靠的（存疑数字），在有效数字中只保留一位不可靠数，这样该轴的测得值为20.015mm。

若用测量范围为275～300mm、分度值为0.01mm、测量误差为±0.009mm的千分尺测轴径，测得值为295.345mm，该轴的真值在（295.345-0.009）～（295.345+0.009）mm范围内，可见测得值小数点后第一位是可靠的，第二位、第三位是不可靠的，只保留一位不可靠数则该轴的测得值为295.34mm。

从第一个非零的数算起，到最末一位数为止所有的数都称为有效数字，有效数字的位数称有效位数，如：

0.00156——三位有效数字；

0.156——三位有效数字；

156——三位有效数字；

2.103——四位有效数字；

6500——四位有效数字。

在判断有效数字时，0这个数字是特殊的，它可能是有效数字，也可能不是有效数字。当0处在非0数字之前，它不是有效数字，如：

0.35——两位有效数字；

0.082——两位有效数字。

当0处在有效数字中间时，均为有效数字，如：

6016——四位有效数字；

0.082——三位有效数字；

1003——四位有效数字。

当0处在有效数字的末尾时，均为有效数字，如：

1200——四位有效数字；

210.10——五位有效数字。(www.xing528.com)

2.有效数字处理原则

当有效数字位数确定后，最后一位有效数字的确定原则如下：

1）末位有效数字后的第一位有效数字大于5，则末位有效数字加1，小于5舍去不计。

2）末位有效数字后的第一位数字等于5时，则将末位有效数字凑成偶数（当末位有效数字为奇数时加1；末位有效数字为偶数时不变）。

例如，若有效数字保留到小数点后第三位，其有效数字如下：

3.14159——有效数字3.142；

2.71729——有效数字2.717；

4.51050——有效数字4.510；

3.21650——有效数字3.216；

5.6235——有效数字5.624。

3）在加减法运算中，保留小数点后的位数应取各数中小数点后位数最少的，例如：

60.43+12.317+5.022-77.769≈77.77；

60.43-58.308=2.122≈2.12。

4）在乘除运算中，取有效位数最少的，如：

2352×0.211=496.272≈496；

0.0222×34.5×2.01=1.539459≈1.54。

5）在对数运算中，对数的位数应与真数有效数字的位数相等。

6）在乘方运算中，乘方值的有效数字位数应与底数的有效数字位数相同。

7）在开方运算中，有效数字位数应与被开方数的有效数字位数相同。

8）对某些数学常数如π、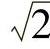等参与运算时，按以上方法确定其有效数字位数。但为保证最终运算结果的精度，对这些常数可适当多选1～2位。

9）对测量极限误差、标准偏差等表示测量精度的数值，只取一位或两位有效数字，且末位数应与它所对应的测量结果的末位数一致。例如，34.0234±0.00021应写成34.0234±0.0002。