神经网络控制多电动机同步协调

1.多电动机同步协调控制的原理

对于多电动机同步协调控制系统来说，实现的是电动机转速的跟随，受到扰动后，电动机之间的转速趋于同步越快越好，即应尽快消除转速偏差；当电动机之间的转速趋于同步时，要尽量减小转速发生超调。一般情况下，要求系统中的第i台电动机转速v_i和第i＋l台电动机转速v_i＋1，之间保持一定的比例关系，即v_i＝a·v_i＋1以满足系统的实际工艺要求。这里a为转速同步系数。在实际运行过程中，若要满足系统的同步要求，周期采样获取某一环节的前台电动机转速v_i和后台电动机转速v_i＋1后，v_i和v_i＋1按下式定义转速同步偏差时，表明在同步系数a下，v_i和v_i＋1同步，当e≠0时，表明在同步系统a_f，v_i和v_i＋1不同步。在本方案中采用改进的耦合同步协调控制系统（见图8-21），各电动机采用同一电压给定的基础上，电动机1转速误差Δv₁＝v₁－v_fb1，电动机2的转速误差Δv₂＝v₂－v_fb2，计算某一电动机实际速度和给定速度的偏差e，以及当前的偏差变化量Δe，同步控制器补偿同样采用PID控制。其差值经过PID补偿器加到随动电动机输入端。

2.基于神经网络PID控制器的建立

BP神经网络是应用最广泛的一种人工神经网络，在各门学科领域中都具有很重要的实用价值，根据本系统的控制系统的特点，为了快速消除同步误差，本方案采用BP神经网络与PID相结合的控制作为同步补偿方法。

（1）BP神经网络PID控制系统

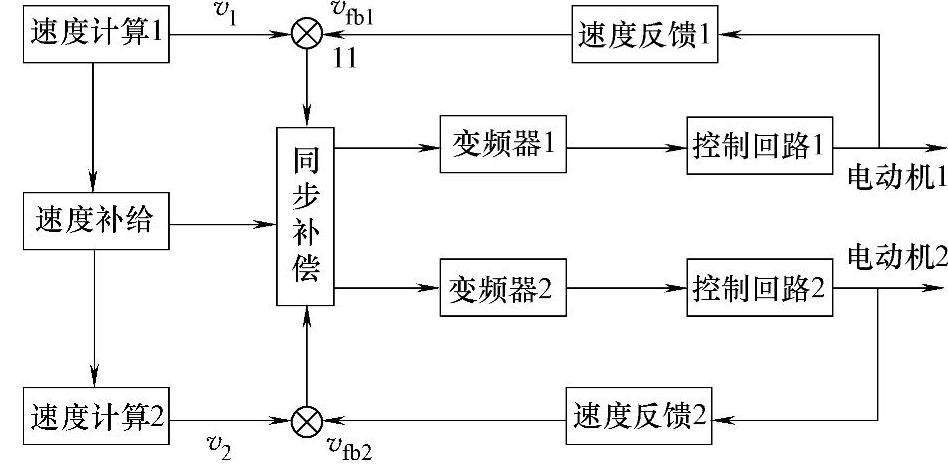
图8-21 改进的耦合多电机同步控制系统

神经网络PID控制系统的结构如图8-22所示，控制器由两部分组成：

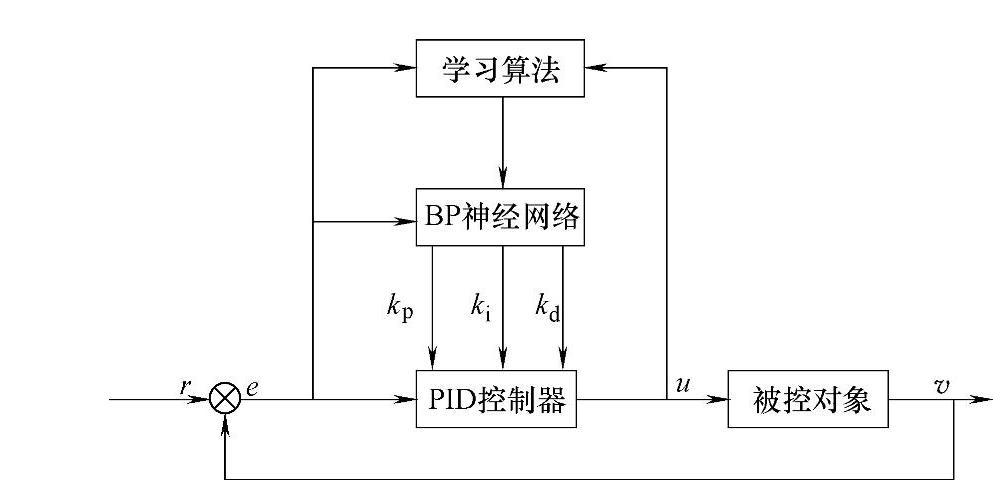
图8-22 神经网络PID控制系统

1）常规PID控制器，直接对被控对象进行闭环控制，并且其控制参数k_p、k_i、k_d为在线调整方式；

2）BP神经网络，根据系统的运行状态，调节PID控制器的参数，以期达到某种性能指标的最优化，使输出层神经元的输出对应于PID控制器的3个可调参数k_p、k_i、k_d。通过BP神经网络的自学习、加权系数的调整，使BP神经网络输出对应于某种最优控制规律下的PID控制器参数。以电动机作为控制对象，一般采用增量式PID控制算法进行控制。它的控制算式为

u（k）＝u（k－1）＋k_p［e（k）－e（k－1）］＋k_ie（k）＋

k_d［e（k）－2e（k－1）＋e（k－2）］ （8-20）

式中 k_p、k_i、k_d——比例、积分、微分系数。

（2）神经网络PID的算法实现(www.xing528.com)

1）训练阶段的工作。

第1步：设计输入输出神经元。该BP神经网络的输入有3个即神经元速度v_i、速度偏差e和偏差变化量Δe，输出层有3个神经元，为PID控制器的3个可调节参数k_p、k_i、k_d。

第2步：设计隐含层神经元个数。该方案初步确定隐含层节点数为5个，学习一定次数后，不成功再增加隐含层节点数，一直达到比较合理的神经元数为止。

第3步：设计神经网络初始值。该方案中，设定的学习次数N＝5000次，误差限定值E＝0.02。

第4步：应用Simulink对BP网络进行训练和仿真。

2）测试阶段的工作。在测试阶段，主要是对训练过的网络输入测试样本，测试网络的学习效果，即判断网络的运算值与样本的期望值之差是否在允许的范围之内。在此不再赘述具体判定过程。

3.仿真与分析

本方案以两台电动机同步为模型进行仿真。在电动机的参数设定时，对两台电动机的参数取相同值。电动机参数为：定子每相绕组电阻R＝5.9Ω，定子d相绕组电感L_d＝0.573H，转子电阻R＝5.6Ω，转子电感L＝0.58H给定角速度ω＝500rad／s，极对数为3。在t＝0.05s时，突加阶跃扰动，利用MATLAB对传统PID和神经网络PID分别进行仿真，得到实验曲线如图8-23，图8-24所示。

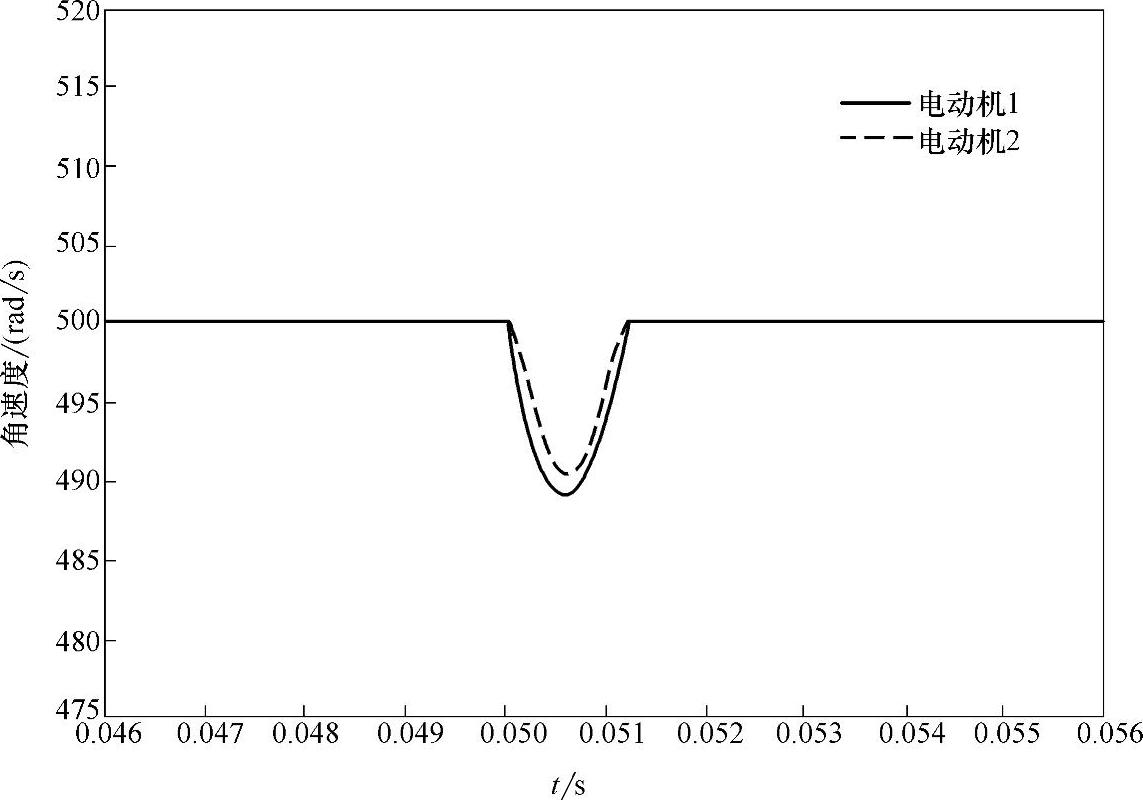
图8-23 传统PID控制响应曲线

比较两种仿真结果，经计算采用常规PID补偿器时，突加负载扰动后，同步误差ΔV_error＝0.26％，采用神经网络PID补偿器时，突加负载扰动后，同步误差ΔV_error.＝0.08％，由此可以看到，采用神经网络PID补偿器方法时，抗干扰性能优于只采用常规PID补偿器时的性能，前者具有更好的控制特性。

4.结束语

该方案针对多电动机同步协调控制中出现的多变量、强耦合、具有大惯性环节、难以建立准确数学模型的被控对象，在传统PID的基础上引入神经网络的概念，将神经网络PID补偿器用于速度同步补偿中，仿真结果表明，本方法使系统的抗干扰能力增强，同步精度有所提高，控制效果良好。

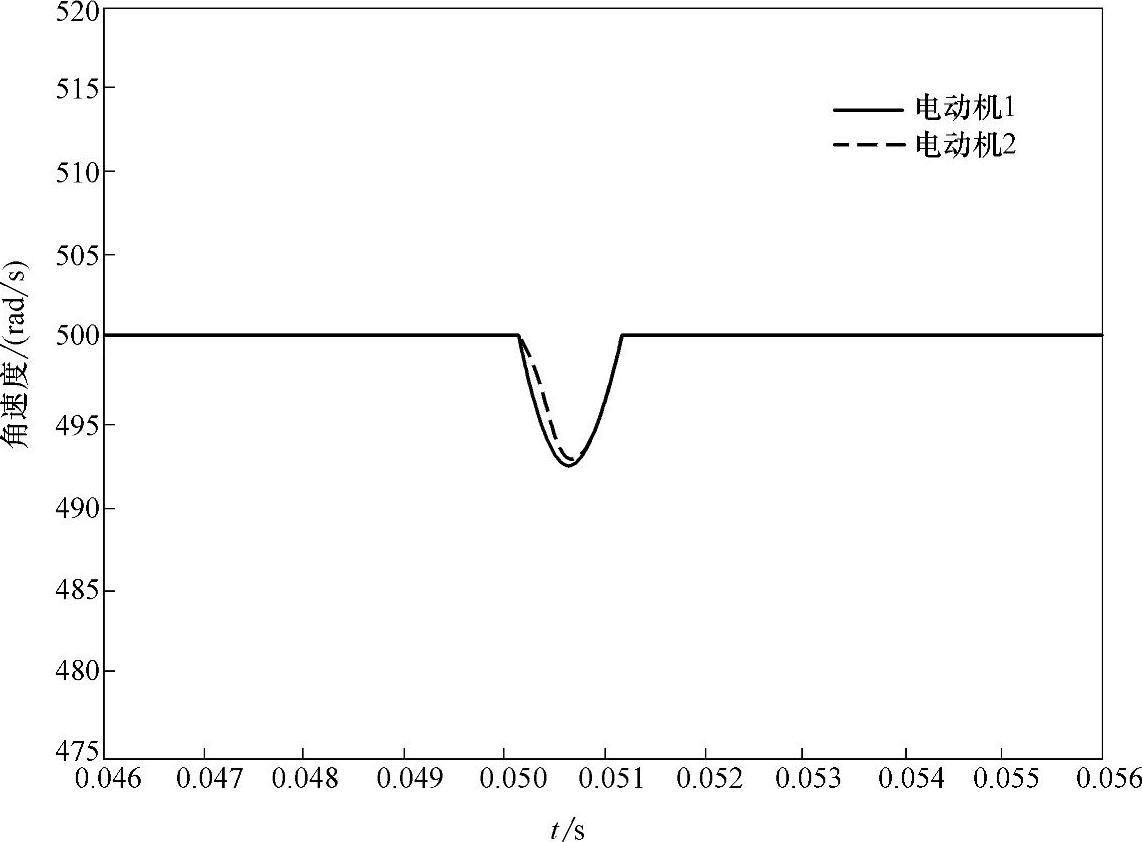
图8-24 神经网络PID控制响应曲线