基于遗传算法的受电弓优化设计

受电弓是电力机车受流的重要装置。受电弓良好的动力性能可以有效减少弓网间的冲击和接触力的变化，从而减少离线率，提高受电弓的跟随性，保证机车安全平稳运行。随着机车的运行速度日益提高，对受电弓的性能要求越来越高。已有文献运用基于梯度的优化方法对受电弓的弓头升弓轨迹、受电弓转矩及弓头平衡杆摆动角度进行了优化。本方案是利用遗传算法优良的全局搜索性能，介绍一种有利于提高受电弓性能的优化设计方法，在工况要求苛刻的条件下，取得了更好的优化结果，并采用虚拟样机技术进行了仿真验证。

1.受电弓机构简化几何模型的建立

图8-5为本节所研究的单臂受电弓机构简化几何关系模型。其基本机构是一个平面四连杆机构，其中下臂杆AD为主动运动构件。优化的过程也就是通过遗传算法寻优计算找到满足给定的各变量取值范围和约束的最优设计变量的过程。

在图8-5所示的机构中，以点A为坐标原点建立参考系，可以得到：

（1）Q点的运动轨迹方程

式中 γ——上框架上部DQ与水平方向的

夹角，是L₁、L₃、L₄、a、b、c和α的函数。

（2）弓头平衡杆QF与竖直方向的夹角：

θ＝arctan［（F_x－x）／（y－F_y）］ （8-8）

式中 F——点F在x方向的坐标，F_x＝L₆ cose－L₅ cos（a－g）；

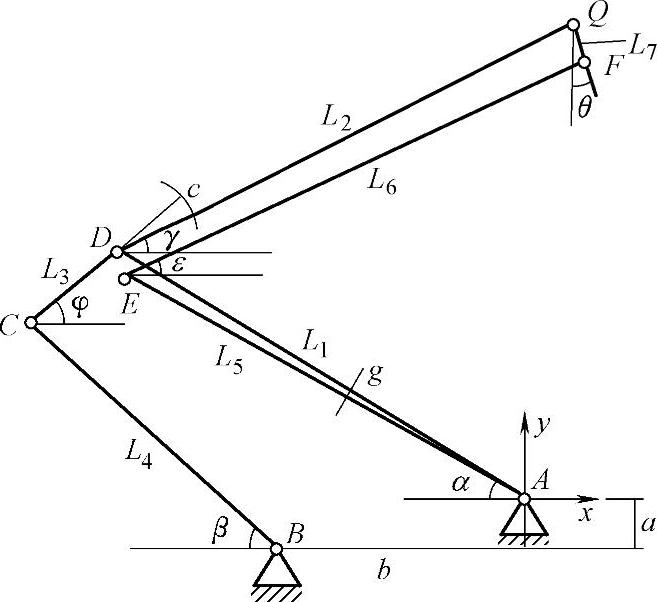
图8-5 单臂受电弓几何关系模型

F_y——点F在y方向的坐标，F_y＝L₆ sine－L₅ sin（a－g）；

e——控制杆EF与水平方向的夹角。

2.受电弓机构几何参数的优化

（1）优化方法的选择及遗传算法

受电弓机构几何参数的优化属于典型的非线性最优化问题，对于此类问题的求解，经典数值算法采用基于梯度的搜索方法。遗传算法与传统优化算法相比。具有隐含并行性，只需要由目标函数值转换得来的适应值信息，而不需要导数等其他信息，搜索过程不易陷入局部最优点，是一种全局寻优算法。

（2）目标函数和约束条件的确定

机车运行过程中，为保证平稳受流，受电弓机构必须能够满足一定的运动要求：

1）受电弓的工作高度有严格规定，如本方案研究的地铁受电弓的工作范围为400～2325mm，收弓高度为300mm。

2）弓头Q点在升弓过程中应作竖直或近似竖直运动。即Q点的运动轨迹在工作高度范围内在机车前进方向（x方向）与理想竖直线的偏差应尽可能小。本方案要求最大偏差不能超过30mm。

3）为了防止弓头前后滑板受力不均，弓头平衡杆QF在工作高度范围内应作近乎平动，从而保证弓头始终处于水平位置，即在升弓过程中，弓头平衡杆摆动角度应尽可能小。

4）升弓转矩应保证在工作范围内弓网之间接触的正压力变化小。本方案规定在工作范围内，弓网接触正压力为（120±10）N。

上述1）、2）、3）是弓头运动轨迹的优化目标，4）是约束条件。

受电弓升弓所需的升弓转矩是受电弓设计中最重要的参数之一，它既是保持良好弓网关系的主要因素，也是匹配升弓弹簧、驱动气缸以及力臂的主要依据，本方案对于升弓转矩要求在一个合适的范围内，能够匹配出升弓弹簧和力臂，而对弓头运动轨迹的要求比较严格。故将弓头运动轨迹在x方向上的偏差作为主要目标，将升弓转矩的目标函数转化为弓头运动轨迹优化问题的约束条件，从而将多目标优化问题转化为单一目标优化问题求解。平衡杆的优化是在完成了弓头运动轨迹优化后进行的。

3.弓头运动轨迹优化目标函数的建立

目标函数为

minf＝x_max－x_min （8-9）

式中 x_max、x_min——分弓头运动轨迹在x方向的最大坐标值与最小坐标值。

（1）约束条件的确定

受电弓工作时需要满足的运动要求就是升弓轨迹优化设计目标函数的约束条件：(www.xing528.com)

y_min≤300mm，y_max≥2325mm（8-10）

L₁∈［1400，1750］ L₂∈［1800，1850］

L₃∈［150，400］ L₄∈［900，1246］

a∈［130，140］ b∈［760，770］

c∈［12，71°，20°］ M_max≤1.65×10⁶ N·mm

上述约束条件中，y_min为受电弓收弓高度；y_max为弓头在工作范围内的最高点（未注单位为mm）。

（2）平衡杆优化的目标函数

如图8-5所示，平衡杆QF与竖直方向的夹角θ即为衡量弓头摆动程度的参数，它在升弓或降弓过程中是不断变化的。在弓头的结构中，设QF与竖直方向的夹角为17°。因此，平衡杆优化的目标函数为

minf＝max（abs（θ－17）） （8-11）

（3）考虑运动及结构工艺要求的约束条件

L₅∈［1400，1570］，L₆∈［1810，1880］

L₇∈［80，120］，g∈［1.0°，2.1°］ （8-12）

4.受电弓几何参数的遗传算法优化

（1）遗传算子及操作

1）编码：经典遗传算法先将个体进行二进制编码，然后操作处理，最后解码为浮点数。这样做的优点是算子操作易于理解、编程方便；缺点是速度受到影响，特别是求解比较复杂的工程实际问题时效果不好。为了提高遗传算法的运行效率，该方案采用的是浮点数编码方式。

2）选择操作：本方案采用联赛选择方法，它的基本思想是：从群体中随机选择一定数目的个体（本方案取4），选择适应度最高的一个个体作为下一代的个体，反复执行直到所选择的个体数目达到预定值。

3）交叉操作：交叉操作是遗传算法中最主要的遗传操作。本方案的一个改进是在交叉算子中同时进行简单交叉、启发式交叉和算术交叉。这样处理能加大交叉的力度，使收敛速度加快。

4）变异操作：一般而言，变异概率P_m取得很小，本方案取0.05。变异操作是十分微妙的遗传操作，它需要和交叉操作配合使用，目的是保持群体中个体的多样性，可以有效克服可能限于局部解的弊端。为加大变异的力度，使收敛速度加快。该方案采用了边界变异、一致变异、非一致变异和多点非一致变异。实际应用表明，这样处理能加大交叉和变异的力度，使收敛速度加快。

5）适应度函数：适应度函数的选取至关重要，直接影响到遗传算法的收敛速度以及能否找到最优解。一般而言，适应度函数是由目标函数变换而成的。该方案分别以受电弓升弓轨迹在机车前进方向上的偏差和弓头平衡杆摆动的角度为适应度函数。

（2）优化结果及其分析

经过改进遗传算法寻优得到受电弓机构几何模型的最优参数，升弓轨迹及平衡杆遗传算法进化曲线如图8-6和图8-7所示。从图中可以看出，用遗传算法优化升弓轨迹、平衡杆时，是快速收敛的。弓头运动轨迹优化结果为升弓角从－2°～39.85°时，f＝26.16，并且y_min＝284.32mm＜300mm，y_max＝2352.7mm，M_max＝1.5488×10⁶ N·mm，达到了设计要求。平衡杆优化结果为在受电弓工作区间内f＝max（abs（θ－17））＝0.36°，也就是说弓头在工作范围内相对于水平面的偏差最大只有0.36°，也达到了设计要求。弓头运动轨迹优化结果如图8-8所示，升弓转矩优化结果如图8-9所示。

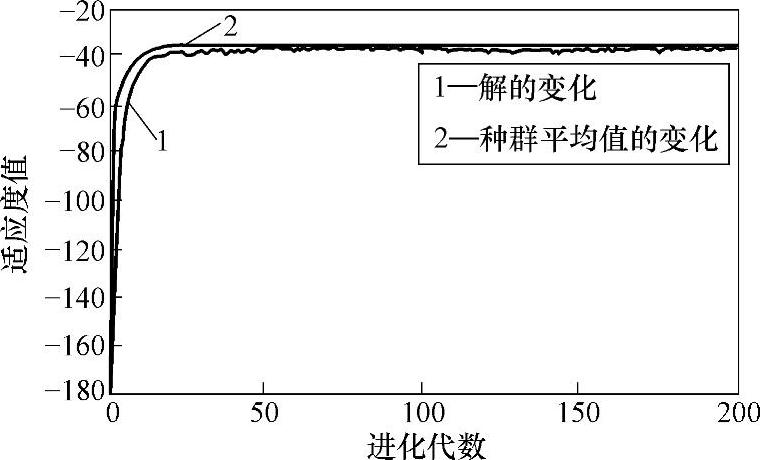
图8-6 升弓轨迹遗传算法优化进化曲线

图8-8 弓头运动轨迹优化结果的比较

弓头摆角的优化结果如图8-10所示。在图8-8、图8-9和图8-10中，以“MATLAB”所标识的曲线为遗传算法的优化结果，以“ADAMS”所标识的曲线为运用虚拟样机技术和优化后的模型对弓头升弓轨迹、升弓转矩和平衡杆摆动角度等参数进行仿真验证的结果。

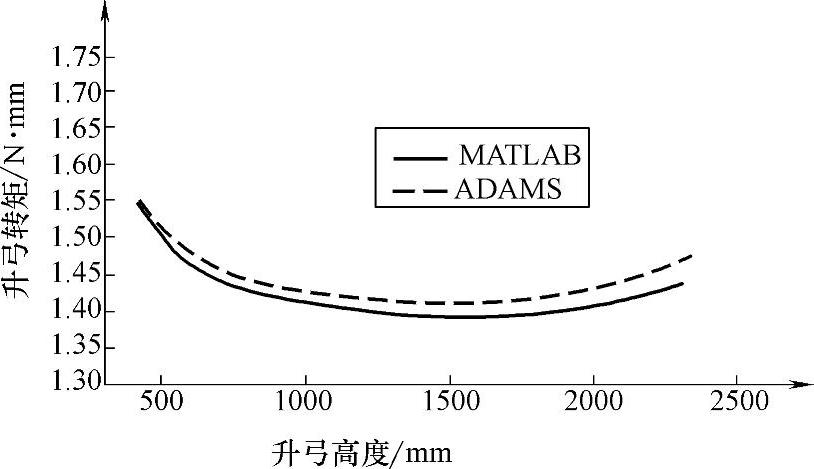
图8-9 升弓转矩优化结果的比较

图8-10 弓头平衡杆摆动角度结果的比较