神经网络自适应控制优化加工过程

由于传统的自适应控制依赖于过程模型，而切削加工过程由于加工参数的影响而具有严重的不确定性和非线性，故传统的自适应控制难以胜任。神经网络具有逼近任意连续有界非线性函数的能力，具有自适应能力，并行处理和高度鲁棒性，采用神经网络方法设计的控制系统具有更快的响应速度，更强的自适应能力和更强的鲁棒性。本方案将神经网络引入传统的加工过程的自适应控制中，形成神经网络自适应控制器，对切削加工过程参量——切削力进行了研究，并通过对神经网络进行自适应调节，不断调节进给速度，从而实现加工过程的恒切削力控制。

1.自适应控制系统结构

图8-1为自适应控制系统结构。它由神经网络控制器、加工过程和切削力加工过程的神经网络自适应控制系统传感器三部分组成。加工过程由计算机数字控制（CNC）伺服系统、机械传动机构、刀具工件系统等组成，为控制系统的执行部分；切削力传感器定时采样实际的切削力F与期望切削力F_r比较形成误差信号，以此来调节神经网络控制器；神经网络控制器的主要功能是根据实际切削力与期望

图8-1 自适应控制系统结构

切削力的误差信号实时调节控制器的输出，即改变进给速度，从而达到恒切削力控制的目的。

2.神经网络控制器的设计

神经网络间接自适应控制框图如图8-2所示。它采用了两个神经网络，一个是神经网络辨识器（NNI），对被控系统进行正向辨识，对被控对象的函数输入进行跟踪，建立一个辅助网络预测其输出；另一个是神经网络控制器（NNC），用来产生合适的控制量，控制误差经过辨识网络反传修正控制器网络权值。

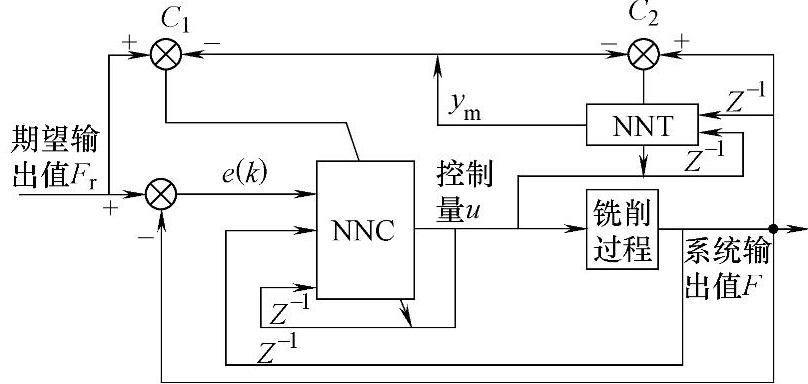
图8-2 神经网络间接自适应控制框图

（1）神经网络辨识（NNI）

神经网络辨识器模型如图8-3所示。

神经网络辨识器采用RBF神经网络。它是一种三层前向网络，由输入到输出的映射是非线性的，隐含层空间到输出空间的映射是线性的，从而大大加快了学习速度，并避免局部极小问题。

在RBF神经网络结构中，x＝［x₁，x₂，…，x_n］为网络的输入矢量（Δu（k），ΔF（k））；y_m为神经网络的输出。

设RBF神经网络的径向基矢量H＝［h₁，h₂，…，h_m］，其中h_j为高斯基函数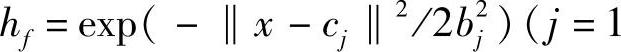，2，…，m），网络的第j个节点的中心矢量为C_j＝［c_j1，c_j2，…，c_jn］。

设网络的基宽矢量B＝［b₁，b₂，…，b_m］，b₁为节点j的基宽度参数，且为大于零的数，网络的权矢量w＝［w₁，w₂，w₃，…，w_m］。

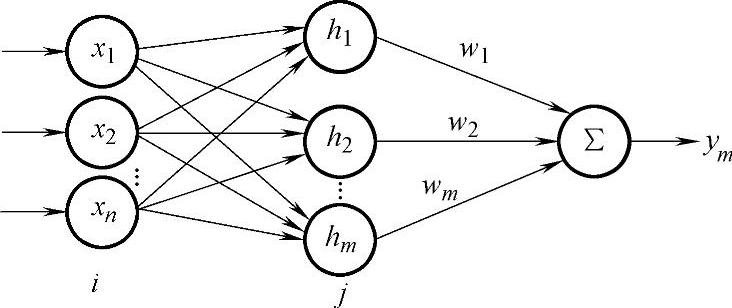
图8-3 RBF神经网络

辨识网络的输出为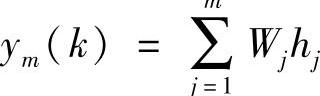，辨识网络的性能指标函数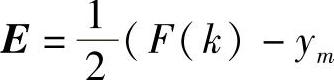（k））2，根据梯度下降法，输出权、节点中心及节点基宽参数的迭代算法如下：

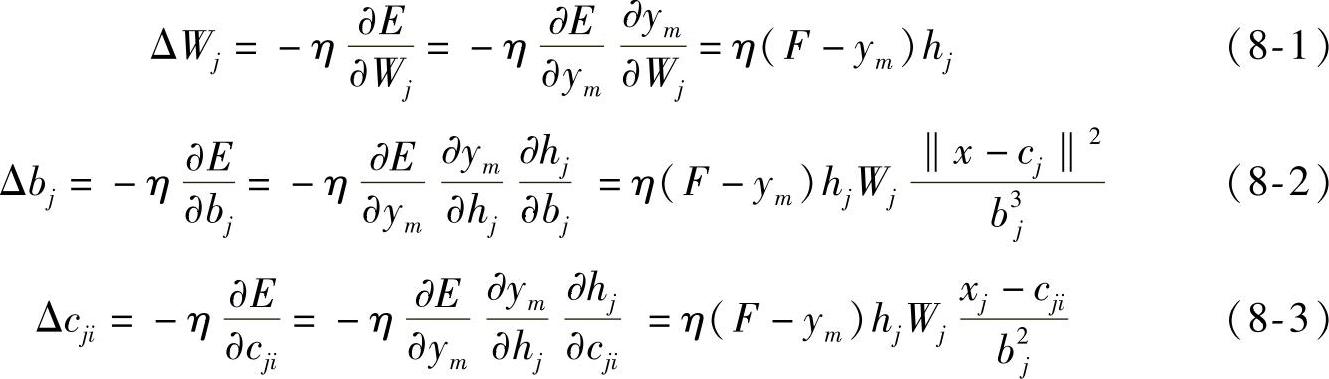
式中 η——学习速率。

（2）神经网络控制器（NNC）

考虑到BP神经网络具有自学习和对任意非线性函数的万能逼近能力，且切削力对加工状态比较敏感，所以采用BP神经网络来对数控铣削加工过程进行控制，在加工过程中不断调节进给速度，以实现恒切削力约束自适应控制，从而提高切削效率。

神经网络控制器采用三层BP神经网络。隐含层和输出层均采用Sigmoid激发函数，之所以选S型函数作为BP网络神经元的激活函数是因为它是连续可微分的。设输入层节点数为p，隐含层节点数为q，输出节点数为1；O_i为网络输入变量，O_j为隐含层输出变量，O为网络输出变量，B_j、B分别为隐含层和输出层神经元的阈值，w_ji、w_j分别为隐含层与输入层、输出层与隐含层节点之间连接权值；net _j和net分别为隐含层和输出层的输入，则有

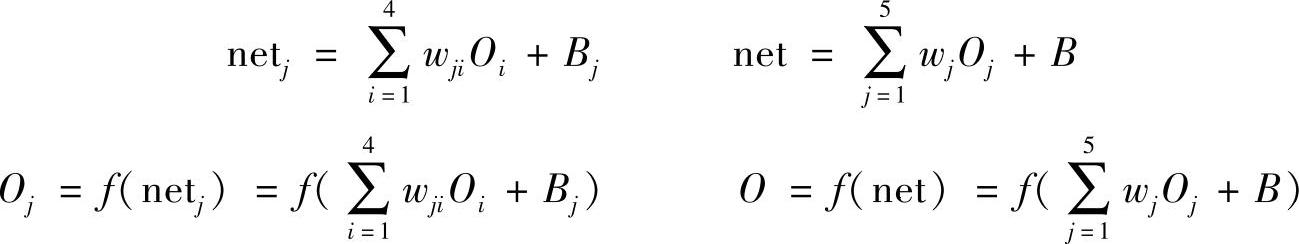
定义系统的误差的二次函数为E＝e（k＋1）2／2＝［F_r（k＋1）－F（k＋1）］²／2，神经网络按E函数梯度变化的反方向进行调整，使网络的输出接近期望输出。(www.xing528.com)

设η为学习速率，η＞0，则有

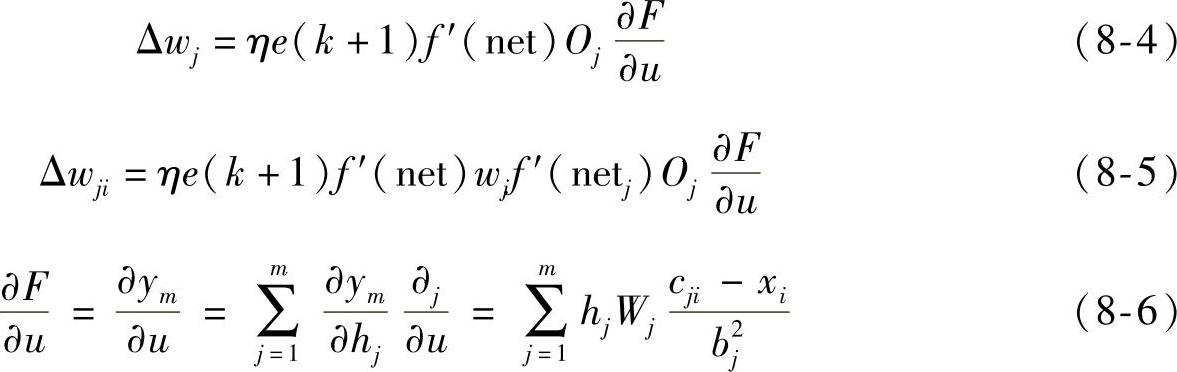
由于BP算法是一个非线性优化问题，缺点是存在局部最小问题，而且学习速度较慢，因此采用改进的BP算法，即通过采用黄金分割变步长，使步长得到合理的调整，即e＝e（k）－e（k－1）＞0时，η（k＋1）＝η（k）×0.618，否则η（k＋1）＝η（k）／0.618。

3.控制算法与实验仿真

（1）控制算法

神经网络自适应控制算法概括为①初始化，置所有权值为较小的随机数；②采样得到F（k）、F_r（k），计算e（k）；③由NNC产生输出u（k），将u（k）送入对象和跟踪神经网络（NN）中，产生下一步的输出F（k＋1）；④按式（8-1）、式（8-2）和式（8-3）修正NNI权值、节点中心及节点基宽；⑤用y_m（k＋1）代替F（k＋1），按式（8-4）、式（8-5）和式（8-6）逐层反传修正NNC的权值；⑥令k＝k＋1，将F（k）、u（k）、e（k）进行移位处理后，返回②，进入下一采样循环。

（2）系统仿真

该方案以铣削加工为对象，在主轴转速恒定、铣削深度作阶跃变化的条件下，通过检测铣削力，自动调节进给速度，使加工过程中切削力维持在设定的期望值水平。

神经网络控制器采用4-9-1和2-5-1的神经网络结构。

加工过程模型为

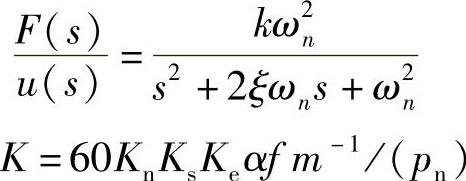
式中 K_s——切削比力（N／mm²）；

K_n——伺服增益（mm／（V.s））；

K_e——测力仪转换系数；

α——被吃刀量（mm）；

f——进给量（mm／r）；

p——铣削时刀具的齿数；

n——主轴转速（r／mm）。

各参数设置为n＝600r／min，K_n＝1mm／（V·s），K_s＝1670N／mm²，K_e＝1.5，ξ＝0.5，ω_n＝20rad／s，m＝0.7，F_r＝1000N，T＝0.01s。假设被吃刀量在1～5mm之间变化。

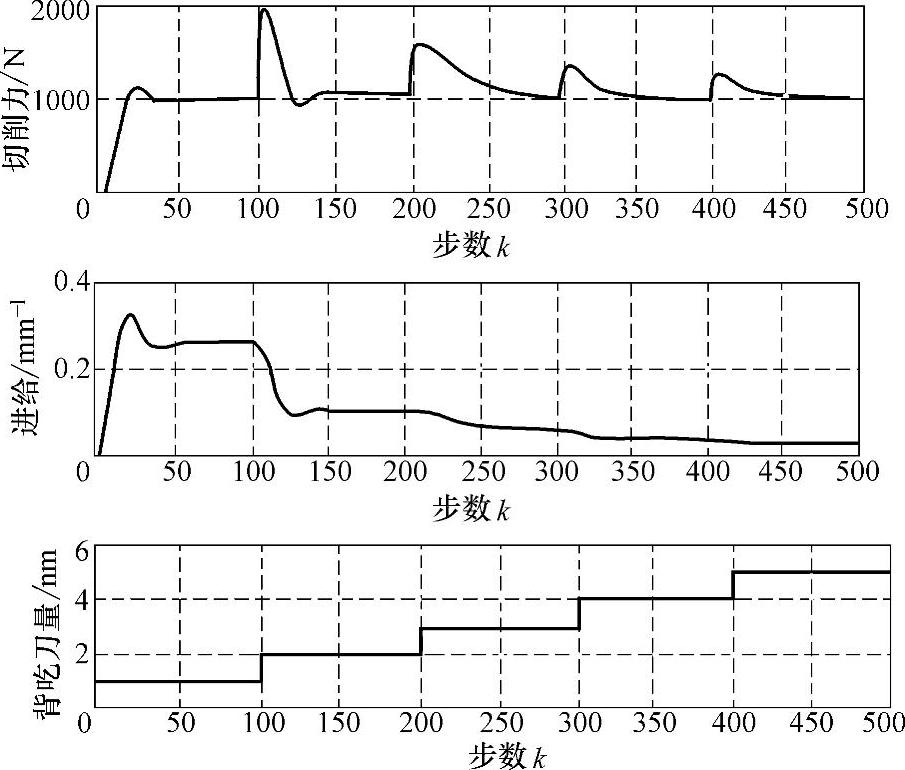
图8-4 神经网络间接自适应控制仿真结果

仿真效果如图8-4所示。从图中可以看出，开始切削时，实际切削功率大于设定值，神经网络控制器经过几个采样周期的学习后，迅速调节进给速度，使铣削功率很快跟踪设定值。在切深发生突变时，为适应负载变化，神经网络控制器调节进给速度，来达到自适应控制的目的。仿真结果表明，随着加工状态的变化不断调整进给速度，从而使系统维持在最佳工作状态。从仿真结果看，系统的超调量较大，但实际加工时系统的超调量要小得多，因为刀具是渐进切入的，而仿真时背吃刀量是瞬时变化的，可见神经网络控制器具有较强的自适应能力和鲁棒性。

4.结论

传统的自适应控制在解决非线性控制系统时，难以建立精确的数学模型，且由于对象和环境的不确定性，往往难以达到满意的控制效果。该设计方案实现了加工过程的神经网络自适应控制，它以实际切削力为反馈信号，通过实时调节进给速度来实现恒切削力控制，这是一项有益的尝试。仿真结果表明，将神经网络用作加工过程的控制器，将使整个加工过程具有很强的处理未知非线性被控对象的能力，而且控制性能良好，自适应能力强，系统方案有效可行。