遗传算法优化电动机直接转矩控制：模糊自适应异步实现

1.引言

鉴于传统的PID控制器满足不了系统在时变情况下响应速度快、稳态精度高的要求，本方案设计了一种自适应模糊PI速度调节器，用模糊控制器推断出PI控制器的参数，以适应于高精度控制的要求，并根据模糊转矩控制系统中速度的实时变化趋势，通过遗传算法（GA）和参数调整算法对模糊控制器的量化因子和比例因子进行优化处理和调整，其中采用遗传算法离线粗调、参数调整算法在线优化细调，较好地解决了变参数非线性直接转矩控制系统的控制问题。

2.采用遗传算法的模糊自适应PI控制器的直接转矩控制系统结构

直接转矩控制的基本原理是通过对电动机定子磁链和转矩的输出值与给定值之间的偏差选择逆变器的开关状态，以实现对转矩的直接控制。基于遗传算法的模糊自适应控制的直接转矩控制系统的基本结构如图7-22所示。

图7-22所示的系统中，采用了两个模糊控制器，其一是用模糊控制器取代了常规直接转矩控制系统的磁链和转矩控制器。其中转矩偏差e_T、磁链偏差eψ和位置角θ为模糊控制器的3个输入变量。通过引入模糊控制逻辑后，区分e_T和eψ的大小作不同的决策来优化开关状态，从而改善系统性能；定子磁链和转矩观测器用来完成定子电流和定子电压的3／2变换及观测。其二是速度调节器采用基于遗传算法的模糊自适应PI控制器，用模糊逻辑控制规律自适应地调节PI控制器的参数，而模糊控制器本身的参数则用遗传算法和参数调整算法分别进行离线粗调和在线细调。

图7-22 基于遗传算法的模糊自适应控制的直接转矩控制系统的基本结构

3.基于遗传算法的模糊自适应PI速度调节器的设计

基于遗传算法的模糊自适应PI速度调节器框图如图7-23所示。

图7-23 速度调节器框图

已有的一些文献提出了一些自适应的模糊控制方法，其中大多数都采用固定的量化因子和比例因子，但在对实际系统进行模糊控制时，采用固定值系统往往达不到预期的控制效果，产生过渡过程时间长或振荡现象，它们对系统的动静态性能影响很大，因此若能对其进行在线的修正，系统的性能可进一步改善。本方案针对这一问题，根据异步电动机的运行特点，提出了一种基于遗传算法的模糊自适应PI控制器作为直接转矩控制系统的速度调节器的方法，其设计过程分为基本模糊控制器的设计和遗传算法优化模糊控制器因子设计两个步骤。其中基本模糊控制器用来调整PI控制器的参数，再结合遗传算法和参数调整算法对模糊控制器的量化因子和比例因子分别进行离线粗调和在线细调。

（1）基本模糊控制器的设计

PI控制器的离散表达式如下：

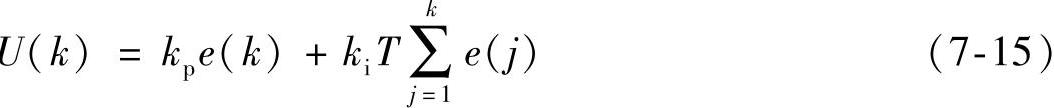
图7-24 变量隶属函数

a）偏差隶属函数

b）偏差变化隶属函数

c）输出隶属函数

式中 T——采样周期；

e（k）——输入量；

k_p、k_i——控制器参数。

在一般的转速调节设计中，通常把系统校正成典型Ⅱ型系统，经计算得到k_p、k_i，然后进行微调，而此处系统模型完全未知，可先用扩充响应曲线法得到k_p、k_i的大致范围，即［k_pmin，k_pmax］和［k_imin，k_imax］。为了方便寻找，可实时推理出恰当的PI参数控制规律，对于参数k_p、k_i，通过下面的线性变换使得k_p、k_i归一到［0，1］区间：

k_p′＝（k_p－k_pmin）／（k_pmax^－kpmin）

k_i′＝（k_i－k_imin）／（k_imax^－k imin） （7-16）

显然，如能确定k_p′、k_i′，就可以十分容易地求出系统参数k_p、k_i。

选取转速偏差e和偏差变化率Δe为输入变量，e＝n∗－n，Δe＝de／dt，其中n∗为转速给定值，n为转速反馈值，通过量化因子k_e和k_c将其从基本论域转换到模糊集论域中。输出控制量为PI参数k_p′、k_i′。E为转速偏差的语言变量，其在论域上的取值为｛NB，NM，NMS，NSS，ZE-RO，PSS，PMS，PM，PB｝；EC为偏差变化率的语言变量，其在论域上的取值为｛ZERO，NE，PO｝；U_p、U_i分别为输出｛ZERO，SS，MS，M，B｝。隶属函数选对称、均匀分布、全交叠的三角形隶属函数，如图7-24所示。

模糊控制器的控制规则可由e、Δe和k′_p、k′_i来描述，第j条控制规则R_i可写成

IF e＝A_j AND Δe＝B_j，THEN k_p′＝U_pj，k_i′＝U_ij （7-17）

其中，i＝27（即共有27条规则），A_j、B_j，U_pj和U_ij分别属于各自的模糊子集。

采用单点模糊化、乘积推理和重心法清晰化所得的k时刻的模糊控制器的输出结果为

并将U_p、U_I分别乘比例因子k_up、k_uI作用于被控对象。

控制规则的生成是通过分析经典PI控制的阶跃响应，根据过渡过程的要求和专家经验得来的。图7-25为直接转矩控制系统的阶跃响应曲线。

为了获得控制规则，需要对图7-25所示曲线进行分段分析。

1）在0点控制的起始阶段，为削弱各物理量初始变化的冲击，应适当地减小k_p。

2）在a点前，e（k）很大，为了提高系统的快速性能，要求输出很大，故此时k_p应置大。

图7-25 直接转矩控制的阶跃响应曲线

3）当k_p使速度调节器的输出进入饱和状态时，再增大k_p是没有意义的，为了使超调量控制在系统设定范围内，此时k_i应置较小。

4）较大的偏差经过积分后将造成过b点时仍有很大的给定值，带来较大的超调量。为了减小超调量，输出响应从a点至b点时间中，k_p应逐步减小，在b点前要退出饱和区。

5）为了消除静态误差，当正向超调量达到c点时，为了加快系统的稳定，此时k_i应逐步增加。

依此类推，通过各阶段响应的分析，可以得到系统在不同的状况时，PI控制器有关参数的修正系数k_p′、k_i′模糊控制规则。控制规则见表7-1、表7-2。

表7-1 U_p的模糊控制规则表

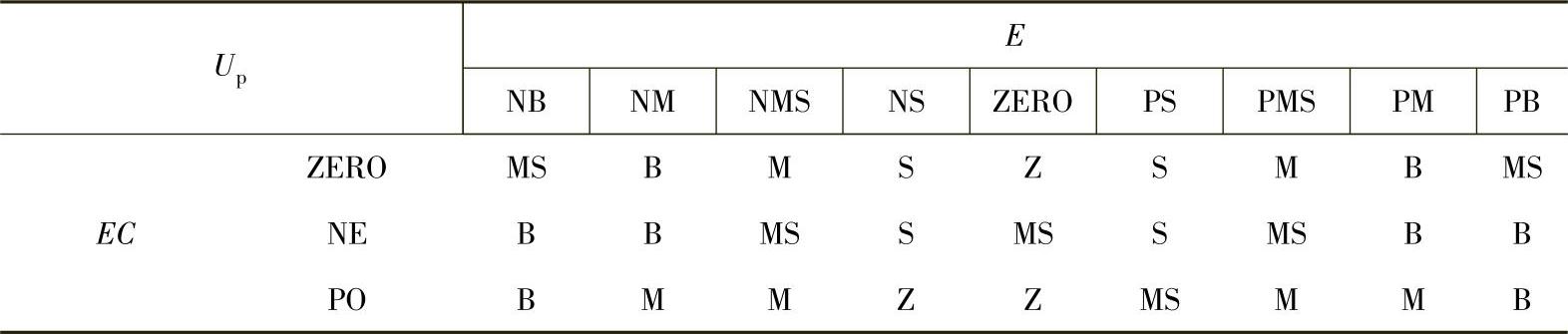
表7-2 U_I的模糊控制规则表

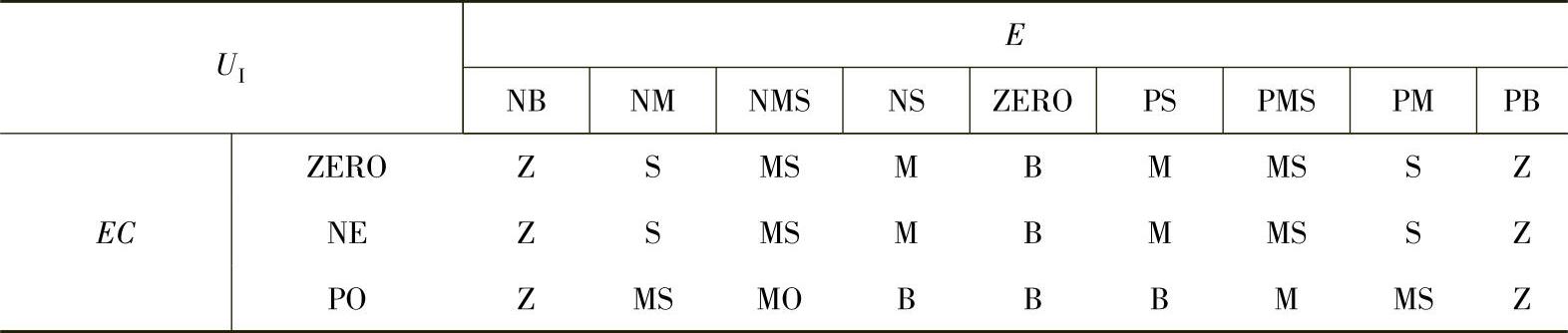
（2）遗传算法优化模糊控制器因子设计(www.xing528.com)

量化因子k_e、k_c和比例因子k_up、k_ui对模糊控制器的控制性能有很大影响，本方案采用遗传算法对它们进行优化。常规模糊控制器的量化因子和比例因子的选择往往根据经验，并不能获得最优的搭配，本方案采用遗传算法离线获得因子的最优初值，再在此初值的基础上用参数调整算法对其进行在线的优化细调。

1）遗传算法具体设计步骤：

① 编码。需要优化的参数个数为4，采用的编码方法为串联二进制映射编码法，它将每个参数都用一定长度的二进制串进行编码，然后再将各参数的编码连接形成1个组合代码串。每个参数用6位无符号二进制码表示，每个个体长度l＝24位，从左到右依次为k_e、k_c和k_uP、k_uI的二进制码。设参数取值范围的上下限为p_max.j和p_min.j，则参数串的表示值和实际参数值之间的关系为

式中 i——参数个数，该方案中控制器参数个数为4，故此2^i－1＝2³；

R——一个（i－1）位二进制串所表示的二进制整数。

② 适配度函数。适配度函数是遗传算法应用的关键，直接影响到遗传算法的

收敛度以及能否找到最优解。研究表明，这种目标函数用于控制系统的优化，效果很好。由于遗传操作是根据适值大小进行的，且适值是非负的，而目标函数的优化方向应对应于适值增加的方向，所以采用界限构造法作出改进，选用下式作为适值函数：

在运行遗传算法程序时，需要事先选择的参数包括种群的大小n、交叉概率P_c、变异概率P_m等，这些参数对遗传算法的性能都有很大的影响。

2）种群大小。在使用遗传算法时，首先需要解决的是确定种群的大小，如果太小，不能保证种群中个体的多样性，寻优空间小，导致提前收敛；反之，如果太大，刚增加计算负担，降低了遗传算法的效率，一般选择较大数目的初始种群，可同时处理更多的解，而容易找到全局最优解，其缺点是增加了每次迭代的时间，一般种群大小取编码长度的2倍，即n＝2l＝48。

3）交叉和变异。交叉概率P_c和变异概率P_m的选择是影响遗传算法行为和性能的关键。P_c和P_m设计计算采用自适应遗传算法（Adaptive GA），P_c和P_m能够随适应度自动改变。

P_c设计计算按下式进行：

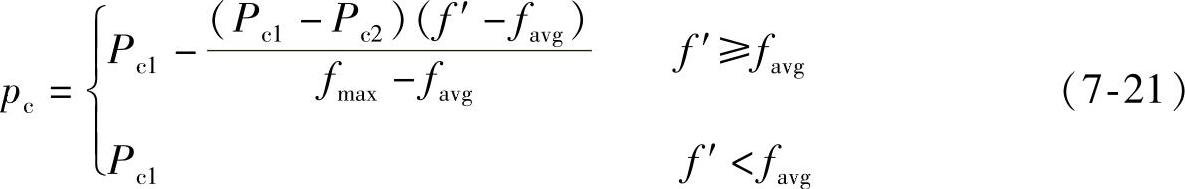
式中 f_max——群体中的最大适应度；

f_avg——每代群体中的平均适应度；

f′——交叉的两个个体中的较大的适应度；

f——变异个体的适应度。

在式（7-21）中，交叉率随父串适应值自动变化，适应值大的个体选用小的交叉率，对于适应值小的个体采用大的交叉率，如此，既保证了不破坏高适应值的个体，又对低适应值的个体采用较高的交叉率，可以提高空间搜索能力，故此一般取值范围定为P_c1＝0.9，P_c2＝0.6。

P_m设计计算按下式进行：

变异概率P_m的选取对GA的性能影响较大，变异算子的引入，一方面将使GA具有局部的随机搜索能力，当GA通过交叉算子已接近最优解邻域时，利用变异算子的这种局部搜索能力可以加速向最优解收敛，此时P_m应取小，否则接近最优解的积木块（Building Block）会因变异而遭破坏；另一方面使GA维持群体多样性，以防止出现过早收敛现象，此时P_m应取大，一般选择在0.001～0.1之间，故此取值范围P_m1＝0.1，P_m2＝0.001。在这里采用了一种P_m的自适应策略，即P_m不是固定不变，而是随着群体中个体的多样性程度而自适应调整。

（3）在线参数调整算法

在遗传算法获得最优初值的基础上，采用如下一组修正量化因子和比例因子的条件语句：

亦即在常规模糊控制器的基础上，引入一个辅助控制器，根据控制过程中偏差和偏差变化率的大小及关系，产生一个控制量来实时地在线修改量化因子及比例因子，以获得更好的系统控制性能。从以上条件语句可知，因子的大小随当前时刻的偏差及偏差变化率的大小而改变。其中A、B、C、D为量化因子k_e、k_c和比例因子k_up、k_ui的修正因子，λ为系统输出接近稳定时存在的偏差量值，k_e（0）、k_c（0）、k_up（0）、k_ui（0）分别表示量化因子和比例因子的初始值，其由遗传算法离线优化获得。k_e′（0）、k_c′（0）、k′_up（0）、k_u′_i（0）分别为k_e（0）、k_c（0）、k_up（0）、k_ui（0）的可调整微增量值，根据系统情况选取，本方案选

k_e′（0）＝k_e（0）／10；k_c′（0）＝k_c（0）／5；k_u′_p（0）＝k_up（0）／5；k_u′_i（0）＝k_ui（0／5）

A、B、C、D可根据系统的特性及经验选取。参数调整算法如下：

分别表示当前和上一时刻的量化因子和比例因子。

4.仿真试验结果与分析

为了验证上述分析和设计的正确性和有效性，对图7-24所示的采用基于遗传算法模糊自适应PI速度调节器的直接转矩控制系统在MATLAB环境下用Simulink搭建模型，在此基础上进行了仿真研究。仿真用电动机参数为P_e＝1.1kW，R_s＝0.435Ω，R_r＝0.81Ω，L_s＝L_r＝0.002H，p_n＝2，J＝0.019kg·m²，L_m＝0.06931H，额定转速n＝1460r·min^－1，试验给定转速n＝1000r·min^－1。

对模糊控制器参数的调节，则按设置的各项遗传算法的参数，经过95次迭代后得到最优解结果，k_c（0）＝10.13，k_c（0）＝1.86，k_up（0）＝1.23，k_ui（0）＝1.16。

系统速度响应、运行磁链圆图、起动过程转矩响应仿真曲线和图形如图7-26～图7-30所示。在图7-26中，虚线为常规模糊PI控制速度响应仿真曲线，实线为基于GA的模糊PI控制速度响应仿真曲线（注：在t_r期间，实线与虚线相重合）。

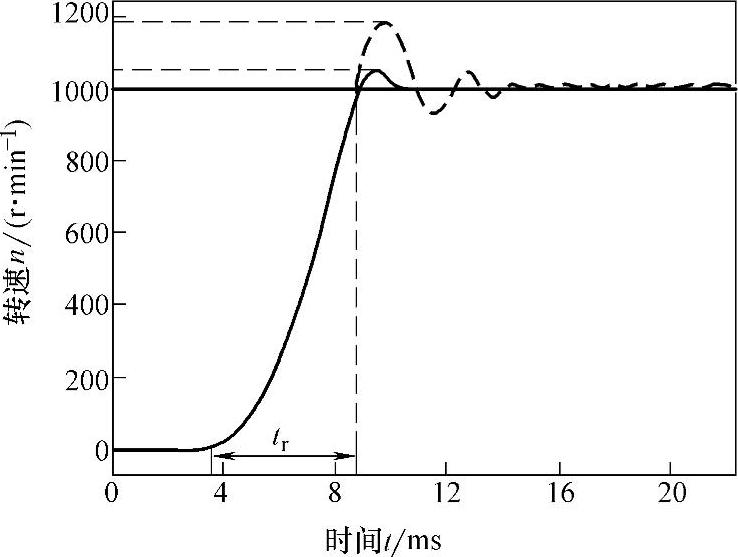
图7-26 速度响应仿真曲线

图7-27 F.DTC运行磁链圆图

图7-28 GA.F.DTC运行磁链圆图

图7-29 F.DTC起动过程转矩响应曲线

图7-30 GA.F.DTC起动过程转矩响应曲线

从图7-26中可以看出，与常规模糊PI调节器相比较，采用基于遗传算法模糊PI调节器的DTC系统，上升时间没有大的改变（均为0.0045s），但其调节时间仅为常规模糊PI调节器的30％，超调量为5％，而采用常规模糊调节器的DTC系统的超调量为20％；图7-27、图7-28表明GA.F.DTC运行磁链圆图的畸变程度略小于F.DTC运行磁链圆图；图7-29、图7-30表明GA.F.DTC起动过程转矩响应快于F.DTC起动过程转矩响应。

从以上仿真试验结果可以看出，采用基于遗传算法的模糊自适应控制DTC的主要性能明显优于一般模糊自适应控制DTC。

5.结论

本方案提出的基于遗传算法自适应模糊PI速度调节器，用模糊控制器推断出PI控制器的参数，可以适应高精度的控制要求。根据模糊直接转矩控制系统中速度的实时变化趋势，遗传算法（GA）和在线参数调整算法对模糊控制器的量化因子和比例因子进行优化处理和调整，较好地解决了变参数非线性直接转矩控制系统起动过程中转速的动态控制问题。仿真的结果表明，它与采用常规模糊PI调节器相比较，在起动阶段电磁转矩的动态响应更快，到达给定转速的时间更短，超调量更小，也使系统获得了更强的鲁棒性。