免疫遗传模糊神经网络控制永磁同步电机

1.引言

永磁同步电动机（PMSM）具有体积小、损耗低、响应快、效率高、可靠性好以及对外界环境适应性强等优点，目前在高性能电气传动系统中得到广泛的应用。但由于它的多变量、严重非线性、参数时变及耦合性强，往往还受到负载干扰、自身的非线性等诸多不确定因素影响，导致其抗干扰能力差，影响PMSM控制性能。PMSM矢量控制是一种高性能的控制策略，但控制性能的好坏主要取决于控制器的设计。传统的PI控制器是以被控对象的数学模型为设计依据，尽管其控制算法简单、鲁棒性好，并有一定的控制精度，但它毕竟是一种线性控制，不能很好地满足存在严重非线性的PMSM系统高精度、快速响应的要求。为此，本方案结合模糊逻辑控制和神经网络的优缺点，以递归模糊神经网络取代原来的BP网络，形成一种新的模糊神经网络——递归模糊神经网络（RFNN），将RFNN控制器作为速度调节器应用于PMSM矢量控制调速系统中，并利用免疫遗传算法（IGA）在线优化RFNN控制器中的参数。仿真结果表明：本方案所述的模糊神经网络速度控制器应用于永磁同步电动机矢量控制系统，能实现精确的速度控制，具有良好的抗干扰性能和较强的鲁棒性。

图7-15 永磁同步电动机空间矢量图

2.PMSM数学模型

图7-15是一台两极永磁同步电动机的空间矢量图。矢量控制的基本原则是把电动机的定子电流分解为直轴电流分量和交轴电流分量。对永磁同步电动机来说，一种有效的矢量控制策略就是通过保持定子电流的直轴分量为零，电磁转矩与定子电流的交轴分量几成正比，以实现良好的线性解耦控制效果。

永磁同步电动机的dq轴模型的电压方程为

永磁同步电动机的磁链方程为

永磁同步电动机的电磁转矩为

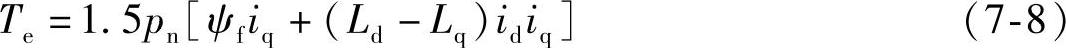
式中u_d，u_q——dq轴定子电压；

R_s——dq轴定子三相绕组电压，

L_d，L_q——dq轴定子绕组电感；

p_n——电动机极对数；

ψ_f——永磁体磁链；

ω_r——转子电角速度。

3.基于IGA优化的递归模糊神经网络控制PMSM矢量调速系统

（1）系统原理与结构

在分析永磁同步电动机数学模型基础上，本方案所述的基于递归模糊神经网速度控制器的PMSM矢量控制系统结构模型如图7-16所示。

该控制系统包含一个速度外环和两个电流内环，电流环通过对i_d和i_q的解耦控制实现转矩控制。速度环的作用是增强系统抗负载扰动的能力，并决定系统的运行性能。利用递归模糊神经网络控制器取代速度环上传统的PI控制器，作为永磁同步电动机闭环矢量控制系统的转速调节器，并采用免疫遗传算法在线优化递归模糊神经网络的参数，从而极大地提高了系统的响应速度、控制精度及鲁棒性能。

调速系统采用交－直－交电压型变压变频技术方案，PWM技术使用空间矢量脉宽调制（SVPWM）法，目的是减少逆变器输出电流的谐波成分及电动机的谐波损耗，降低转矩脉动，从而使永磁同步电动机获得幅值恒定的圆形磁场，即正弦磁通。

图7-16 PMSM矢量控制系统结构模型

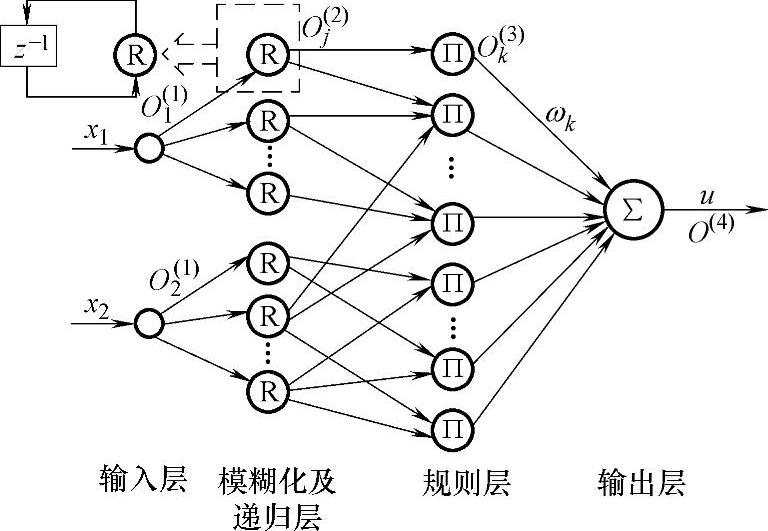
图7-17 递归模糊神经网络结构

（2）递归模糊神经网络控制器

该系统采用具有研究动态特性的递归模糊神经网络（RFNN）控制器结构，如图7-17所示。

它是由4层BP网络组成，即输入层、模糊化及递归层、规则层、解模糊化及输出层，其中在第2层引入递归神经元，递归神经元有内部反馈链接，它以反馈链接的形式存储内部信息，使网络输出不仅取决于当前输入，而且还取决于过去的输入和输出，从而形成局部或全局递归的网络结构，能够有效地处理动态系统的非线性映射问题，具有较快的收敛速度和较少的神经元数目，并进一步简化了网络模型。

第1层：输入层。将输入矢量x＝［e，ec］^T引入网络，每个神经元的输入量均换算在模糊域［－1，1］内。此层输出节点为

第2层：模糊化及递归层。模糊化输入变量，每个输入采用5个模糊语言变量（PB，PS，0，NS，NB｝表示，分别为模糊集的负大、负小、零、正小、正大，计算各输入分量属于各语言变量值模糊集合的隶属函数。这里隶属函数采用高斯基函数来表示。该层共有10个节点，其输出节点为

式中，a_ij，b_ij——高斯基函数的中心值和宽度。

此层每个节点都具有相同结构的递归节点，此层输入节点为

式中r_ij——递归单元的连接权；(www.xing528.com)

O_ij^（2）（t－1）——该层前一时刻的输出。

第3层：模糊控制规则层。“Ⅱ”表示模糊AND操作，这里用“×”乘积实现模糊的“AND”运算。此层共有25个节点，其输入节点为

输出节点为

O_k^（3）＝I_k^（3）

第4层：去模糊化及输出层。实现解模糊操作，计算所有规则的输出之和，并作归一化处理。

此层输入节点为

式中 w_k——第3层（规则层）与第4层（输出层）之间的连接权值。

（3）基于IGA优化的递归模糊神经网络控制器的实现

由于递归模糊神经网络的梯度信息不容易获取，所以基于非梯度的遗传算法成为递归模糊神经网络学习的重要手段之一。免疫遗传算法（IGA）是近年来基于生物免疫机制的一种改进遗传算法，是一种新型的计算智能方法，它是在遗传算法的基础上融合了生物免疫系统的抗原识别、抗体多样性、免疫记忆、浓度控制等机制。解决实际问题时，在保持抗体多样性的情况下，找出针对该抗原的抗体，即问题的解。与标准遗传算法相比，IGA具有以下显著优势：①免疫记忆功能，该功能可以加快搜索速度，提高遗传算法的总体搜索能力；②抗体多样性保持功能，该功能可以提高遗传算法的局部搜索能力；③自我调节功能，该功能可提高遗传算法的局部搜索能力，避免陷入局部最优解。

该系统中，免疫遗传算法的输入为参考模型的输出ω_r与转子实际输出电角速度ω之间的偏差e及其偏差变化率ec₀先将递归模糊神经网络控制器作为系统转速调节器，再利用免疫遗传算法在线优化递归模糊神经网络参数，其中包括第3、4层间的连接权值ω_k、第2层的高斯基函数的中心值a_ij0和宽度b_ij0，以及第2层的递归单元的连接权r_ij、第2、3层之间的连接权值ω_jk等。因此应用免疫遗传算法对网络进行训练、在线优化和调整上述参数，能使递归模糊神经网络控制器具有良好的控制性能，并且对系统参数变化和外界负载扰动具有较强的鲁棒性。

4.IGA算法的设计与实现

IGA算法的设计与实现有如下几步：

1）读入初始化条件，将给定的特定问题视为抗原，并对其进行具体分析，找出最基本的特征信息，确定待优化变量a_ij、b_ij、ω_k、r_ij等。

2）确定IGA的运行参数：群体规模M_pov＝30，交叉概率P_c＝0.8，变异概率P_m＝0.02。

3）产生初始群体（抗体）并编码。如果是记忆中的抗原，则从记忆细胞中取出相应的抗体组成IGA的初始群体，否则随机生成初始群体。选择一定的编码方案（本系统采用十进制）对其编码，组成基因码串，每一码串代表一个个体，表示优化问题的一个解。本系统可选择（a_ij、b_ij、ω_k、r_ij）为每一抗体对应的网络结构参数，共有m组（m＝1，2，…，m）作为初始抗体群体。

4）适应度计算。按编码规则，计算每个抗体的适应度。由于进化只能向着使适应度函数值增大的方向进行，因而适应度函数是以构造目标函数倒数的形式给出。设抗体P_s对应的网络的能量函数为E_s，则适应度函数F_s为

式中 ξ——大于0的常数；

M——训练样本（抗体）总数；

O——输出节点数；

T_jⁿ、Y_jⁿ——第n个训练样本在第j个输出节点的期望输出和实际输出。

5）改变记忆细胞。若是新抗原，则利用当前种群中适应度高的抗体替换记忆细胞中适应度低的抗体；否则，将当前种群中适应度高的抗体加入记忆细胞中。

6）抗体的促进和抑制。计算当前种群中适应度值相近的抗体浓度，即相近抗体数与群体总数的比值。若抗体的浓度较高，则减小抗体的选择概率（即抑制）；反之，则加大抗体的选择概率（即促进），以此来保持种群中个体的多样性。

7）抗体进化操作（交叉和变异）。按交叉概率P_c。和变异概率P_m二进行与标准遗传算法（SGA）相同的交叉和变异操作，对产生的新一代群体重新进行评价、选择、交叉和变异等操作，如此循环重复，不断提高群体最优抗体的适应值和平均适应值，直至最优抗体的适应值达到规定的范围，或最优抗体适应值和群体抗体的平均适应值不再提高，同时满足各项约束条件，则其迭代过程收敛，便输出结果，IGA算法结束。

5.仿真结果分析

分别用传统PI控制器和递归模糊神经网络（RFNN）控制器作为永磁同步电动机（PMSM）矢量控制系统的转速调节器，应用MATLAB／Simulink建立PMSM矢量控制系统的仿真模型，并进行仿真实验。仿真中，永磁同步电动机参数：额定功率为500W，额定相电压为220V，额定转速为1500r／min；定子d轴电感L_d＝0.027H，q轴电感L_q＝0.067H，定子相绕组电阻R_s＝4.495Ω，转动惯量J＝0.00179kg·m²，极对数p＝2。电流调节器选用PI调节器，其参数：k_p＝2，k_i＝35。系统在给定转n_r＝150r／min、负载转矩T_L＝2N·m时起动，并在t＝0.75时给电动机加一个10N·m负载，其响应曲线如图7-18所示。

图7-18中，曲线①、②分别表示PI控制器和RFNN控制器作用下的转速响应曲线。从图7-18中可以看出，无论是响应速度还是超调量，曲线②均优于曲线①，说明递归模糊神经网络控制器能对被控对象实现较好的控制效果。

为了测试在应用免疫遗传算法优化方法后递归模糊神经网络控制器的控制性能，仿真时给定速度指令和负载转矩设置仍同上。图7-19a、b分别为该情况下的转速响应曲线和转矩响应曲线。可以明显观察到，转速在达到稳态时仅比给定转速的指令值略有下降，大约为1448r／min，误差很小。图7-19b中转矩曲线变化比较平滑，即使在负载发生突变时，转矩变化也较平缓，超调量较小。

图7-18 速度响应曲线

图7-19 基于IGA的RFNN控制器的转速和转矩响应曲线

仿真结果表明，基于IGA的递归模糊神经网络控制器与常规PI控制器和RFNN控制器相比，能更好地适应被控参数变化，具有更快的响应速度、更高的稳态精度和更强的抗扰动能力，显示其很强的鲁棒性。

6.结论

以基于免疫遗传算法的递归模糊神经网络控制器取代传统的PI控制器应用于永磁同步电动机的矢量控制系统，使用该控制器作为速度调节器对永磁同步电动机进行精确的速度控制。仿真实验结果表明，本方案得到的各项性能指标均优于PI控制和递归模糊神经网络控制方式，具有很好的适应性和很强的鲁棒性，取得了比较理想的控制效果，从而为实现永磁同步电动机的智能化调速控制提供了切实可行的技术方案。