基于神经元控制的SVPWM整流器直接功率控制方法

1.引言

应用直接功率控制（DPC）的三相电压型PWM整流能有效改善电流波形畸变，获得高功率因数，省去了内部电流环，减少了参数调试。此法与感应电动机磁场定向的直接转矩控制相似，基于电压的DPC和基于虚拟磁链定向的DPC三相PWM整流器是通过直接控制整流器输入输出功率，即通过估算功率与给定功率偏差来实时确定开关状态的选择，以实现整流器直流侧和网侧能量的平衡。其控制系统采用功率滞环控制器，且开关频率也不固定。但是这种非定频滞环控制会使整流器运行噪声增加，产生较宽的电磁干扰频带。为此本方案提出了一种基于神经元控制的SVPWM电压型整流器的DPC方案，与传统方案相比，由于该方案中神经元的智能控制能力，使得系统控制简单，输入谐波含量小，功率因数高，动静态性能优良。

2.虚磁链定向原则和整流器功率估算

图6-27示出三相SVPWM整流器主电路拓扑。

由Park变换可知，静止坐标系中，三相正弦电压u_a、u_b、u_c可等效为一按正弦角频率ω旋转的空间电压矢量u_L，虚磁链矢量ψ_L是对u_L的积分。虚磁链定向是在αβ／dq坐标系中，令ψ_L与d轴重合，即Ψ_L＝Ψ_Ld，Ψ_Lq＝0。各矢量关系如图6-28所示。

图6-27 三相SVPWM整流器主电路拓扑

图6-28 虚磁链参考坐标系和各矢量在αβ／dq坐标系中的关系

运用复数定义以及瞬时无功功率的原理，可得到下列三相SVPWM电压型整流器瞬时有功功率和瞬时无功功率计算式：

式中 i_L——整流器网侧电流合成矢量i_L共轭复数。

如果三相电网电压平衡对称，且为正弦波，整流器桥臂输入端电压也平衡对称时，dψ_Ldt＝0，则

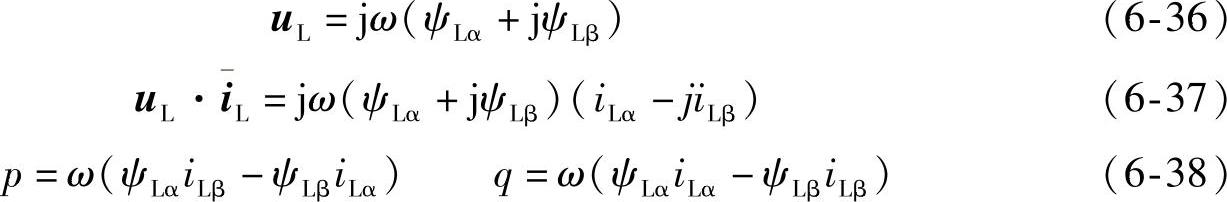
由式（6-38）可见，p与q在一定程度上存在着耦合关系。这样在dq坐标系下，任何一轴的扰动信息就会影响整个系统，所以有必要引入解耦控制方案，以减少这种不利因素。

3.神经元PID控制器

单神经元作为神经网络的基本单位具有学习和自适应能力，而且结构简单、易于计算。对于电动机这种快速响应的系统，控制器选择绝对式的比较合适。另外，在该算法中，要用到除法计算，而且需要调整的控制参数较多。对功率解耦控制而言，由于本身要计算占空比及调整占空比，这些都需要实时运算，因此控制器外需要调整的参数过多也增加了系统设计的复杂程度。所以增量式算法对整流器系统控制参数在线整定有较大的困难。为解决这些矛盾，在此采用绝对式单神经元PID控制器，提出了一种改进的单神经元算法。

神经元输入变为

网络输出为

u（k）＝ω₁x₁（k）＋ω₂x₂（k）＋ω₃x₃（k） （6-40）

这种神经元控制器具有PID控制器的结构，ω₁、ω₂、ω₃对应绝对式PID控制器的K_p、K_i、K_d，通过对其加权系数的调整来实现参数在线整定、参数自适应的功能。加权系数采取有监督学习规则，它与神经元的输入、输出和偏差有关，可定义为

ω_i（k＋1）＝ω_i（k）＋η_ie（k）u（k）x_i（k） （6-41）

在控制器中引入二次性能指标，通过修改权值来使性能指标趋于最小，这是控制最终能够收敛的保证，从而使系统能够最终趋于稳定。根据以往的理论证明，一般引入的二次性能指标为

J＝e（k）2／2 （6-42）

使加权系数的修正沿着J减小的方向，即对ω_i（k）的负梯度方向进行搜索调整。

由于在PID算法中，通常是未知的，可以近似用符号函数sgn取代，这样可得到最终的权值学习规则为

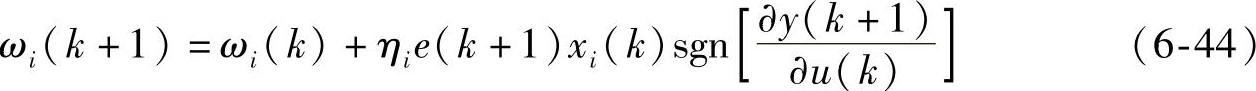
由式（6-40）、式（6-43）可见，该算法结构比较简单，整个算法中需要调整的参数较少，也没有除法计算。由式（6-44）可见，权值的调整算法也比较简单，只须计算加法和乘法。且计算量不大，这对于减少整流器整个系统的运算量有显著意义。

4.DPC-SVM控制原理及框图

图6-29示出基于神经元DPC系统控制框图。(www.xing528.com)

系统采用了SVPWM代替开关逻辑表。p、q与给定的p_ref、q_ref比较后输入PI调节器，得到整流器输入端电压dq轴分量u_sd和u_sq，再经旋转－静止坐标变换，可得αβ坐标系参考电压u_s的αβ分量u_sα，u_sβ，然后利用空间矢量脉宽调制，可得到PWM开关信号对整流器中的开关器件进行控制。

由于ψ_L＝ψ_Ld、ψ_Lq＝0，则三相正弦电压矢量的dq轴分量为

u_Lq＝U_m，u_Ld＝0 （6-45）

式中 U_m——三相正弦电压幅值。

图6-29 SVPWM控制下的DPC框图

根据式（6-45）可知：

p＝U_mi_Lqq＝U_mi_Ld （6-46）

将式（6-46）代入dq坐标系下整流器的数学模型，可以得到

式中 L——整流器电抗器及线路的电感；

R——整流器交流侧等效电阻；

i_Ld、i_Lq——i_L的dq轴分量。

图6-30 SVPWM整流器简化模型

图6-31 有功功率调节器

根据式（6-47），可以得到图6-30所示的整流器简化数学模型。

ωLi_Ld、ωLi_Lq为两功率环间耦合量，稳态时为直流量，根据式（6-45），为实现整流器单位功率因数，需令i_Ld＝0（从而实现q＝0），则有功功率等效控制环如图6-31所示。当交流电源电压稳定时，U_m为恒定值，因而对功率环而言，可视为常值扰动，其扰动可通过PI调节器中的积分成分得到补偿。为了零极点对消和设计方便，令T_n＝R／L＝T_ol，T_ol为系统开环时间常数，是一个很小的量。

5.仿真与试验结果分析

（1）仿真试验

根据图6-29构建基于MATLAB／Simulink环境下的三相电压型SVPWM整流器DPC系统仿真模型，仿真验证了在三相不平衡时的稳态运行波形。仿真电路参数：相电压幅值U_m＝220V，等效电阻R＝0.2Ω，滤波电感L＝8mH，直流侧电容C＝1200μF，R_L＝100Ω。直流电压给定U_d∗_c＝400V，开关调制频率f＝10kHz；功率调节器参数：T_cl＝0.1ms，K_p＝0.4，K_i＝4。三相不平衡电压为

由仿真波型可见，当电源电压三相不平衡时，采用神经元控制，系统网侧电流THD＝0.43％，而传统的PID控制下THD＝7.43％。

（2）样机试验

为了验证上述控制算法的可行性、正确性和可实现性，在此以TMS320F2812DSP为控制核心、MOSFET为功率开关器件制作了SVPWM整流器的实验装置，采用开环控制方式。硬件部分包括主电路、控制电路、电源等。软件部分实现整流级SVPWM控制和神经元参数调整，主要由主程序、下溢中断服务子程序、比较中断服务子程序和捕捉中断服务子程序等构成。

系统参数：三相交流输入相电压有效值为220V；负载输出电阻为150Ω；直流滤波电容为2000μF；调制频率为4kHz；输入电压电流波形如图6-32所示。可见，采用神经元控制下的输入电流谐波含量较低，同时能实现高功率因数运行，实测功率因数λ＝0.98，远高于传统PID控制下的λ值。

图6-32 网侧a相电压电流实际测量波形

a）传统PID控制 b）神经元PID控制

6.结论

由仿真及样机试验波形可见，采用神经元控制时，输入侧的输入电流波形近似正弦波，验证了所提出控制方案的有效性和可行性。试验中，整流部分各开关的占空比由SVPWM算法得出，没有实时地对波形进行调整，所得波形出现部分毛刺，但这可通过闭环控制来解决。