本方案是针对SVPWM逆变器对称调制模式所得的电压矢量选取并非最优而提出来的,采用了生物免疫算法(Immune Algorithm,IA)技术。
1.IA算法理论基础
IA是基于生物免疫机制提出的一种智能计算方法,它将求解问题的目标函数对应为入侵生命体的抗原,而问题的解对应为免疫系统产生的抗体。算法的具体流程如图6-23所示。
(1)编码操作
假设控制对象存在10个变量,IA采用二进制编码,表6-2中的4个染色体为随机产生的解。
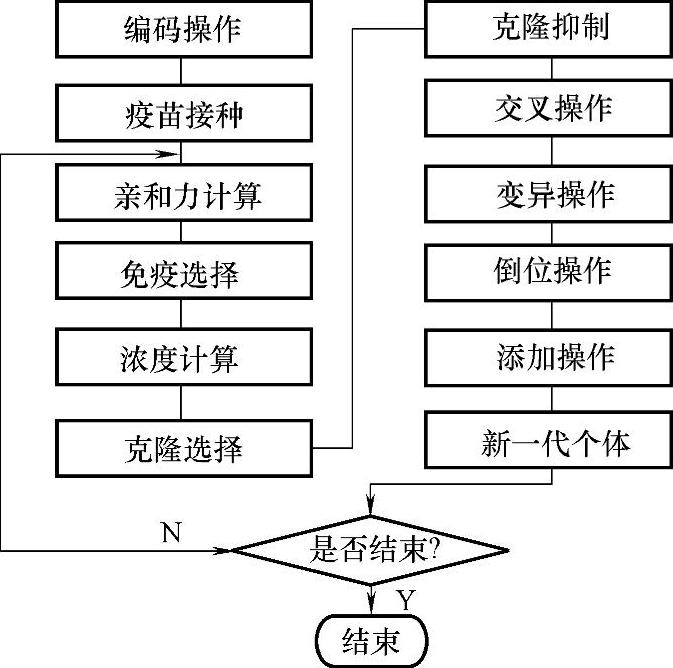
图6-23 算法流程
表6-2 随机产生的抗体

(2)亲和力计算
亲和力是指不同事物的类似程度,分为两类:抗体与抗体的亲和力和抗体与抗原的亲和力。设抗体x通过函数f映射为矢量f(x)。抗体xi和xj通过函数f映射后的空间距离的倒数为xi和xj的亲和力

说明抗体间的空间距离小,亲和力大。
抗体xi和抗原y空间距离的倒数为xi与y的亲和力
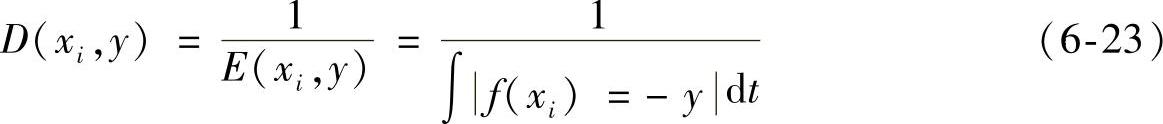
说明抗体与抗原y空间距离较小,亲和力较大。
(3)浓度计算
浓度为抗体xi与全部抗体距离的倒数。
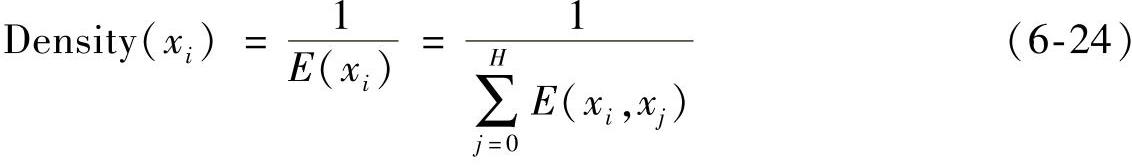
式中 H——种群中抗体总数。
由式(6-24)可得,某个抗体与其他抗体距离越近,则该抗体的浓度越大;距离越远,则浓度越小。
(4)免疫选择
免疫选择是指在抗体群中依据不同抗体的亲和力和浓度对抗体进行选择,该方案的选择函数为
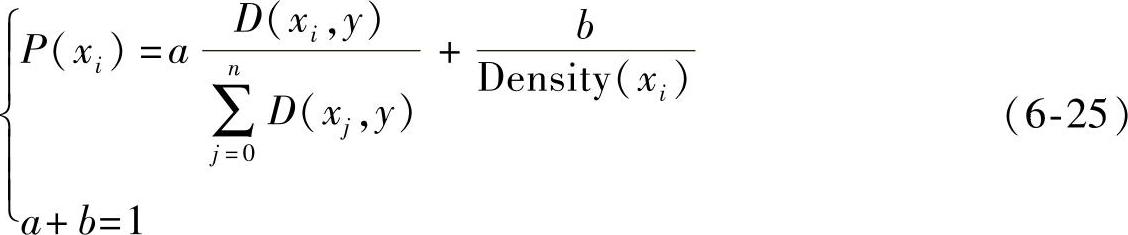
由式(6-25)可知,在浓度一定的条件下,亲和力越大,则选择概率越大;在亲和力一定的条件下,浓度越大,则选择概率越小。这样可确保群体的多样性。假设的各染色体的选择概率见表6-3。
表6-3 不同的选择概率

(5)克隆的选择和抑制
克隆选择是指在抗体群中确定性选择一部分亲和力较高的抗体。克隆抑制是指按抗体亲和力较差抗体进行确定性的抑制,将克隆选择出来的个体替换这类个体。抗体xi的克隆选择和克隆抑制概率为

由式(6-26)、式(6-27)可知,克隆选择操作可保证在种群中亲和力较好的抗体能够被确定性地保留到下一代中。克隆抑制是将亲和力较差的抗体排除出种群。克隆选择和抑制用来模拟抗体之间的互相作用。
(6)疫苗接种
疫苗是由被控对象的先验知识总结得出的。疫苗接种的作用是使抗体以较大概率具有较高适应度。该方案将常规控制策略所得出的控制序列作为疫苗注入IA的初始群体中,可加快算法的收敛速度。
(7)交叉操作
交叉操作是以某一概率相互交换某两个个体之间的部分染色体,具体见表6-4。
表6-4 交叉运算

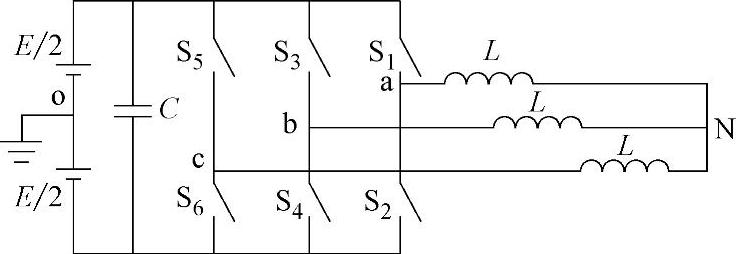
图6-24 三相逆变器主电路
(8)变异操作
变异运算是对个体的某一位基因座上的基因值按照一定概率进行的改变。该方案采用基本位变异方法来进行变异运算。
(9)倒位操作
倒位操作是先随机选中个体的某一位基因,按一定的概率将其和后一位基因相互颠倒位置,生成一个新染色体。抗体xi第y个基因位的倒位概率为
P(y)=β( 6-28)
式中 β——常数;
y——基因位。
(10)添加操作(https://www.xing528.com)
添加操作是指算法在每代以某一概率随机添加新个体。设抗体xi被随机添加的抗体替换的概率为
P(xi)=γ (6-29)
式中 γ——数。
例如个体4“0110110010”被随机产生的新个体“1011001110”替换。
2.IA在三相逆变器最优控制中的应用
(1)三相逆变器主电路
图6-24所示为三相逆变器主电路拓扑。假设电感L为线性电感,Udc=E,S1~S6均为单极性二值逻辑开关,当Sk=1时,k=(1,2,…,6),开关导通;当Sk=0时,开关关断。
根据以上假设可以建立如下方程:

由于三相对称性只需计算(0~120°)期间的控制序列和波形,再经过对称变换,就可得完整周期的控制序列和波形,使得算法的计算效率提高。
将这1/3周期N等分,每小段时间间隔为Δt=2π/(3N),N为自然数,第m个时间段内的输出电流函数为
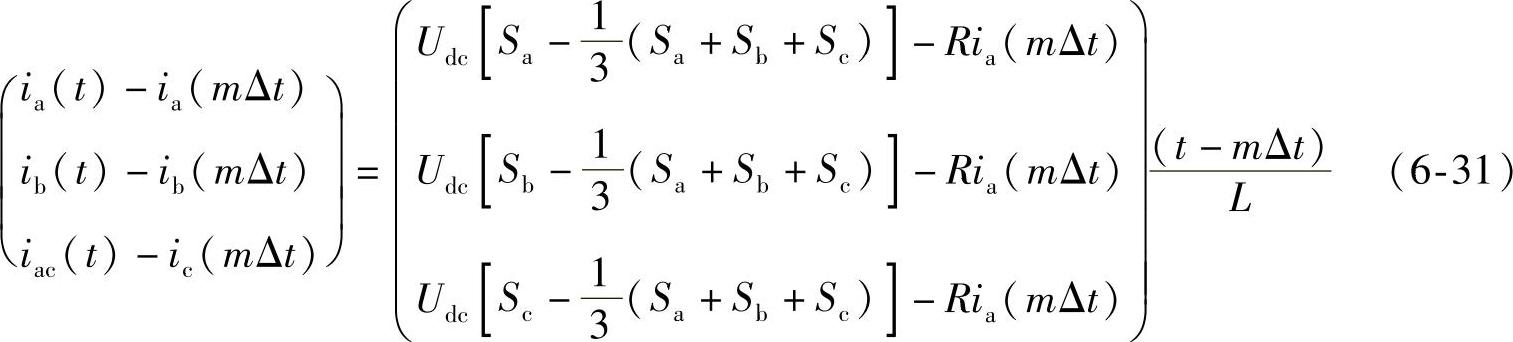
式中 m——时间段,m=0,1,…,N;
ia(mΔt)、ib(mΔt)、ic(mΔt)——A、B、C三相第m个时间段内的电流值。
三相参考电流为
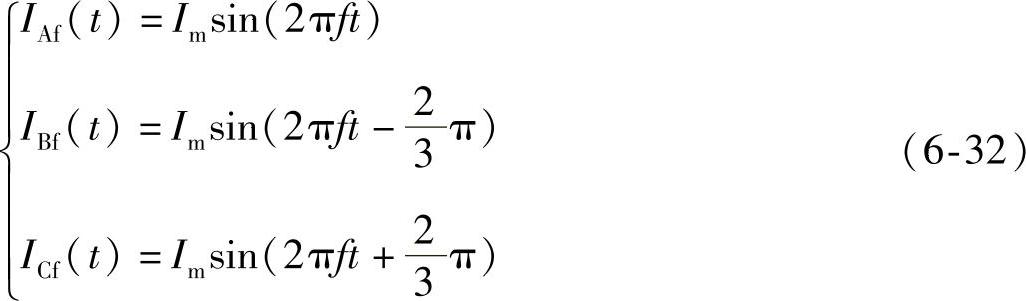
亲和力评价函数
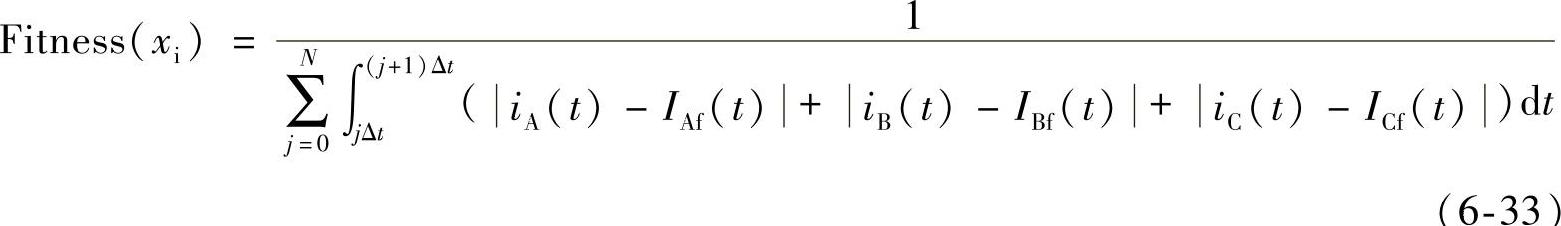
亲和力值越大,说明实际输出波形与参考电流波形的空间距离越小,实际输出波形越好。
(2)逆变器的最优PWM控制矢量
逆变器的最优PWM控制序列包含有控制矢量和作用时间两个部分。控制矢量取值为(000~111)8种情况,作用时间取值范围为(0~166),最小精度为1μs。如果这两个元素均作为优化对象,则算法的收敛时间很长。因此在该方案中是以常规最优波形空间矢量控制为基础,先确定最佳控制矢量,再运用IA计算与之相对应的作用时间,产生最优PWM控制序列。常规最优波形空间矢量控制的控制矢量为“0467640”、“0467640”……。
(3)采用IA计算最优作用时间
根据最佳控制矢量,采用IA来计算矢量的作用时间。在每个控制段内,矢量的作用时间分别为“t1、t2、t3、t4、t5、t6、t7”。每个作用时间的取值范围是(0~Δt),并且满足每个控制段内控制矢量的作用时间之和为Δt,即
t1+t2+t3+t4+t5+t6+t7=Δt
在该方案中,N为40,Δt≈166μs,每个作用时间的取值有(0~166)的167种情况。
(4)仿真
仿真试验主电路如图6-24所示,参数设置如下:参考相电流幅值Im=1A,频率f=50Hz,A相电流初相角为0°。电容两端电压Uc=24.98V,三相电感均为0.0637H。算法参数设置:每代抗体个数为300,抗体含120个基因和120个作用时间变量,交叉率pc=0.7,变异率pm=0.009,倒位率pcom=0.01,选择函数中a=b=0.5。
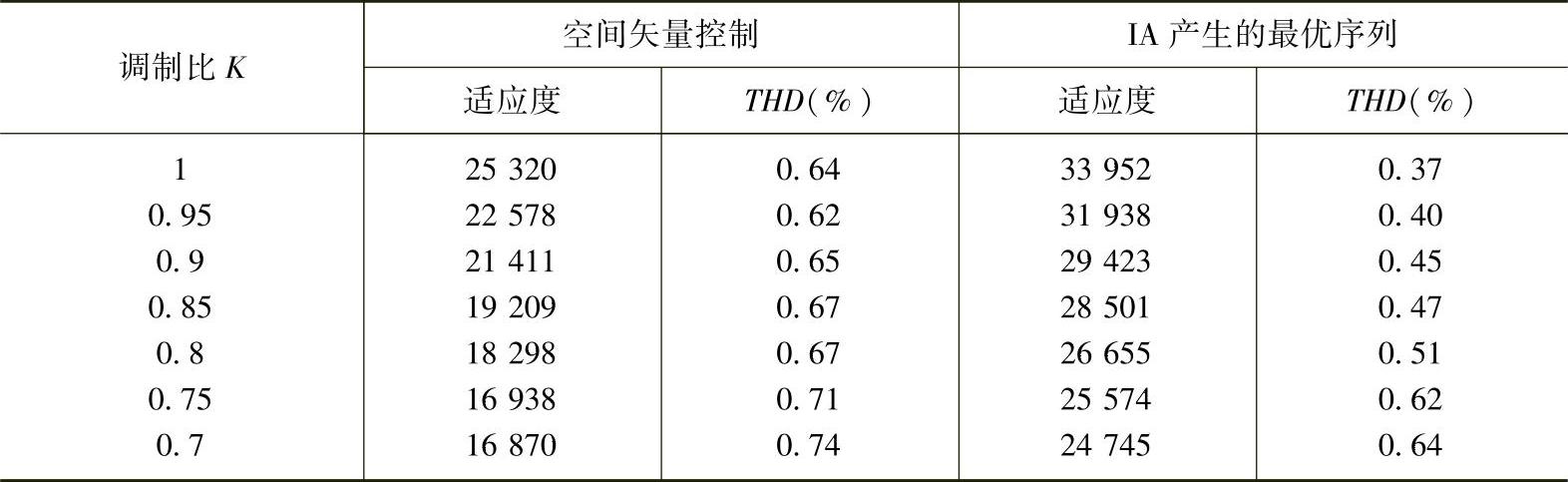
在相同的仿真条件下,根据调制比为1时,空间矢量控制和IA计算出来的最优PWM控制序列下逆变器输出电流波形如图6-25所示,并得出表6-5所示的THD和适应度值。
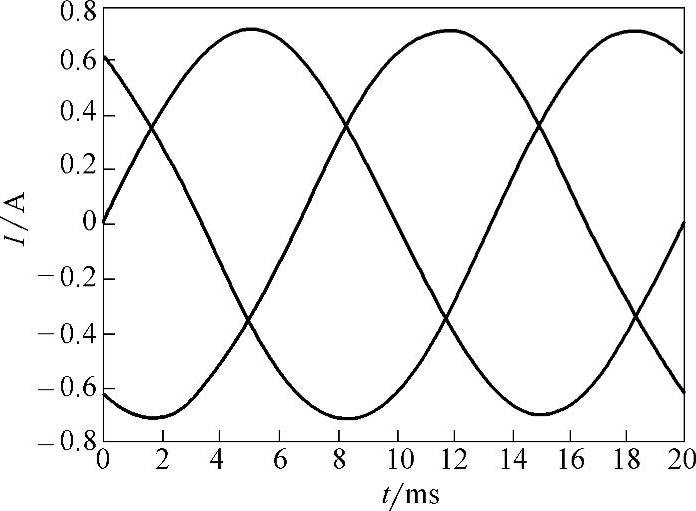
图6-25 最优控制逆变器输出波形
表6-5 不同调制比下两种控制的适应度和THD
前1/3周期的控制矢量为

空间矢量控制所产生的作用时间为

算法所寻找到的最优时间为


空间矢量控制所得到的适应度为25320,最优PWM控制序列的适应度为35953,空间矢量控制输出波形THD=0.64%,免疫算法输出波形THD=0.37%,免疫算法所产生的逆变器控制序列较空间矢量控制在适度应度方面提高42%,在输出波形的总谐波畸变率方面减小了42.19%。
(5)实验结果
不同控制策略逆变器各相电流波形畸变率见表6-6。可以看出,采用IA计算出来的最优控制序列后,逆变器输出三相的电流波形畸变率分别降低21%、25.6%、15.22%。
表6-6 不同控制策略逆变器各相电流波形畸变率

因此可得出结论:应用IA技术所得到的控制序列较常规的控制(对称调制模式)不论在适应度方面还是在波形方面都有明显的改善。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




