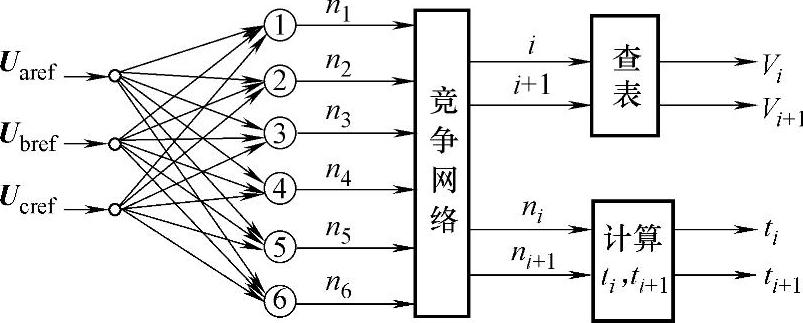
图6-18 反向传播神经网络
本方案是采用反向传播神经网络(CPN)对SVPWM变频器对称调制模式法进行改进的方案。CPN由一个全互连的神经元阵列组成,当外部输入模式出现时,网络的每个神经元都同时工作。网络采用“赢者通吃”的竞争学习机制,完成对复杂模式的分类过程,并在回复(Recalling)模式时,按一定权值来分配模式间的关系,此技术称为CPN-SVM技术。CPN-SVM技术首先判定参考电压Uref处于确定的6个分类模式区域中的哪一个,就可知合成基本电压矢量Uk和Uk+1。CPN-SVM与传统的SVM相一致,也是利用非零矢量将整个平面分为6个扇区。因而,此处的分类模式数为6,是一个确定的量。为此,可省去传统神经网络繁琐的“学习、训练”过程,这一点也正是神经网络引入CPN-SVM的优势所在。
如图6-18所示,在一个神经网络的输入层加上输入矢量U,则6个已确定竞争层的节点,通过竞争的胜者,即为SVPWM中最靠近Uref的主矢量Uk。这样,只需求出最大与次大的,即可得出主、辅矢量Uk和Uk+1。这是借鉴Kohonen神经网络所带来的有益提示。由图6-18可知,竞争层节点ni是参考电压矢量Uaref、Ubref、Ucref的简单的线性组合,根据三相交流可得权值矩阵如式(6-19)所示。其中,第1、2、3列分别为A、B,C三相,正半周为正,负半周为负,最大值取1,左右边各取1/2。权值矩阵的后3行系数符号恰好与上3行系数的符号相反,可进一步减少计算量。

设ni和ni+1为竞争层(竞争网络见图4-18)的胜者,则有
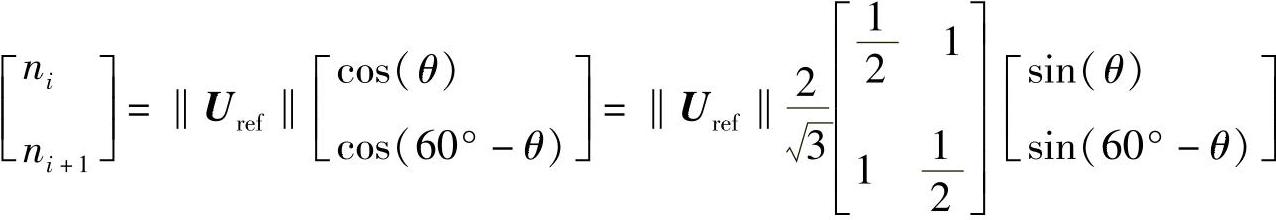
即
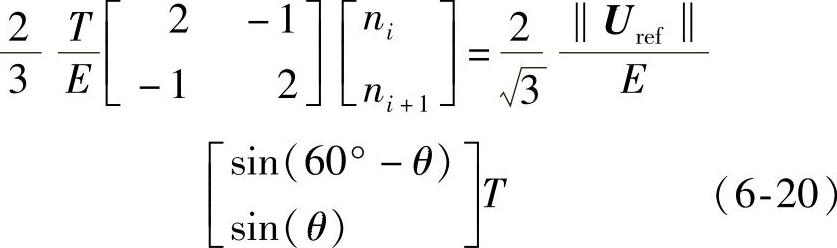
比较式(6-20)即可得
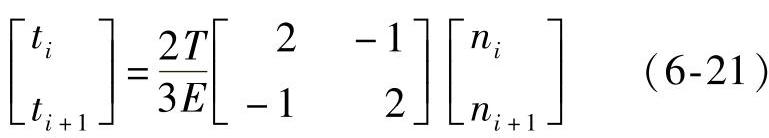
 (https://www.xing528.com)
(https://www.xing528.com)
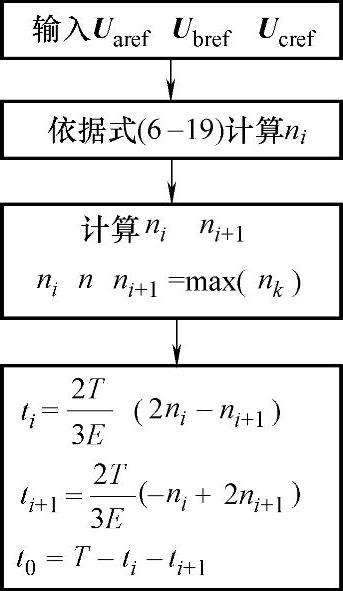
图6-19 CPN-SVM实现流程
CPN-SVM整个计算过程(见图6-19)具体实施步骤如下:①根据式(6-19)计算n1,n2,…,n6;②根据竞争网络选择最大的ni和次大的ni+1,并记录它们的系数i和i+1;③依据式(6-21)计算开关矢量的作用时间ti和ti+1;④根据系数i、i+1查表选择对应的开关矢量,即可确定参考矢量所在的扇区。相对于传统的SVM而言,CPN-SVM所需步骤大大减化,不仅不需要进行Park变换、而且避免了判断扇区所需的反正切函数(或者TI简化算法中的若干次乘法运算),计算作用时间所采用的正弦函数。软件仿真算法采用ode23tb。图6-20a表示直流电压变化曲线,图6-20b表示交流A相电压和电流变化曲线。图6-21是相应的实验波形,图6-22为A相电流频谱,其中n为谐波次数,m为各次谐波幅值与基波幅值之比。其仿真结果与实验结果基本一致,从而验证了该系统能实现高功率因数。
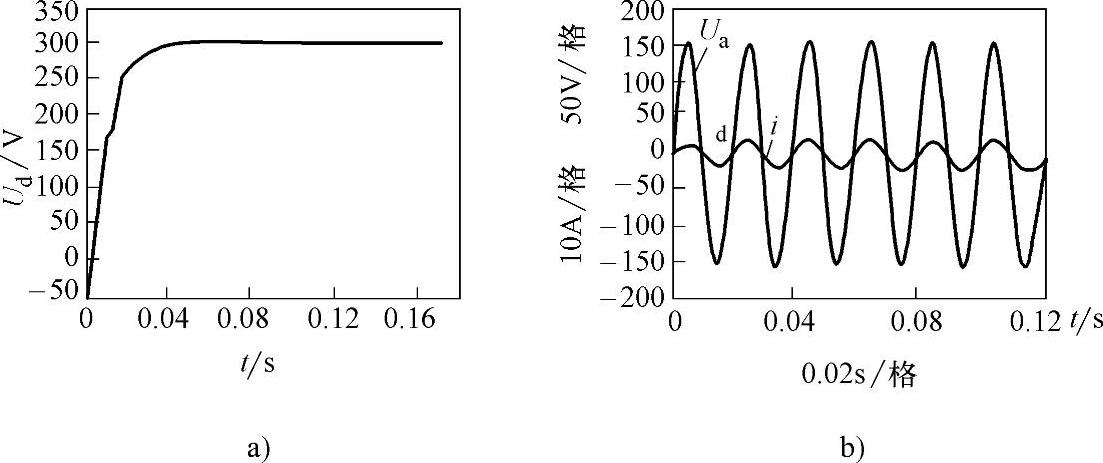
图6-20 基于CPN-SVM的电压型变流器的仿真波形
a)直流电压变化曲线 b)交流A相电压和电流变化曲线
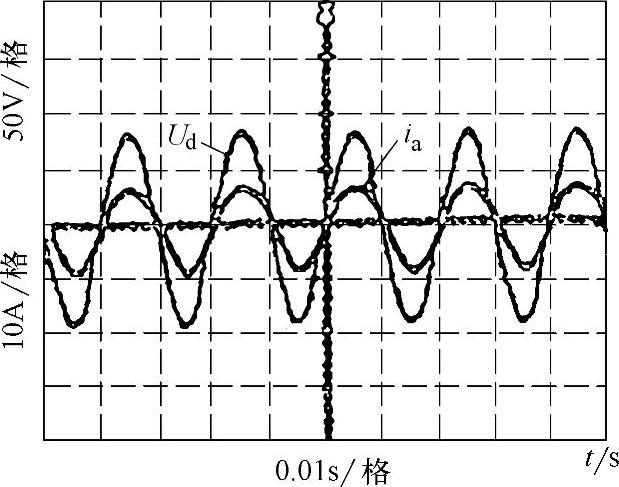
图6-21 基于CPN-SVM的电压型变流器A相电流的实验波形
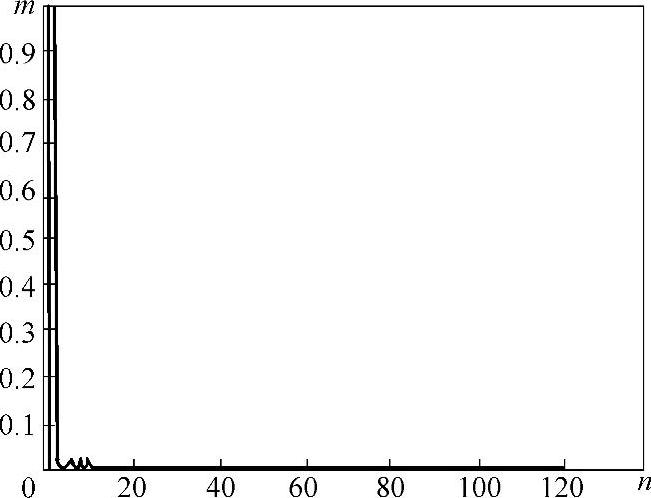
图6-22 A相电流频谱
本方案通过实验可得到下述结论:所提出的基于神经网络的电压型变流器SVM(CPN-SVM)技术的实现是一种非常简单易行的方法,该方法避免了正弦、反正切等非线性运算,缩短了计算时间。基于神经网络SVM控制技术即可实现电压型变流器单位功率因数,能将输出直流电压稳定在一个设定的直流电压值附近,且保持其小纹波特性,是一种应用前景看好的调制方法。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




