使用神经网络控制改善SPWM逆变器的优化

参考文献［3］所述的方案是针对特定谐波消除法的优化方案而提出来的。特定谐波消除法的思路是将最大的低次谐波消去，减小逆变器输出的谐波分量。如消除最大的5、7次谐波，可令其幅值等于零，再与基波的给定一起列成联立方式，解出优化开关角（调制波与载波的交点）。

图6-1所示是消除5、7次两个谐波在π／2时间内3次跳变的波形，图中脉冲的起点和终点的时间叫做开关角，是开关器件开通和关断的时刻，即a₁、a₂，a₃。根据式（6-1）先列出要消去谐波的幅值方程，再联立求解。

图6-1 特定谐波消去法的输出电压波形

给定u₁，即第一个方程等于u∗₁，第2、3两个方程等于0，即u₅＝u₇＝0，再联立解方程可得a₁、a₂和a₃。有了这三个数值，电压波形就可以确定下来，按照所得开关角进行通、断，便可消除5、7次谐波，逆变器输出谐波分量就大大减少了。

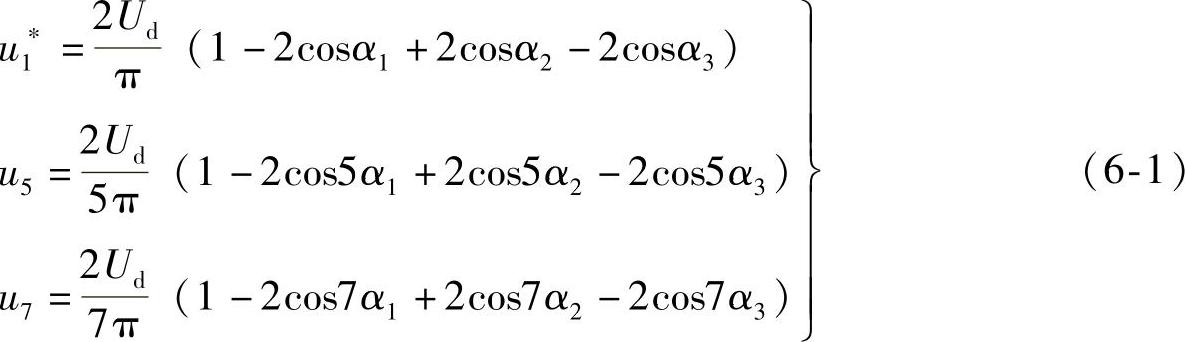
从式（6-1）可知，低次谐波中11、13次谐波幅值也较大，若要进一步消除谐波分量，可再增加两个方程，u₁₁＝u₁₃＝0求出α₁₁、α₁₃便可实现（波形图要重新设计）。

特定谐波消除法的缺点是：由于式（6-1）是超越方程，必须要用计算机计算，并且计算和控制过程十分繁琐，开关频率越高，即m越大，就要解更大的联立超越方程组，并占用很大的内存来存储开关角，所以在开关频率很高的逆变器中很难采用。

再就是，此法是限于稳态最优，负载变动时难以保持；同时不能调压，动态性能欠佳。参考文献［3］所述的方案是不采用式（6-1）求优化开关角的方式，而是找出最优开关角变化规律，采用神经网络控制，确立另一种寻优的方法。

实际上，对最优PWM控制的逆变器而言，在一定的输入电压、输出电压、负载电流和开关角个数下，使逆变器输出电压总谐波含量最小的开关角参数是一定的。也就是说，倘若维持输出电压不变，对于每一组不同的输入电压u_i和输出电流i_o都有一组最优开关角θ_k与之对应，使THD（总谐波畸变率）最小，这就构成了一个一一对应的映射关系。

f_k（u_i，i_o）＝θ_k （6-2）

但函数f_k是一个难以确切描述的非线性函数，且无法得到其确定的代数方程，而原始的在线查表法由于数据量巨大实际上不可行。

神经网络控制具有很强的适应复杂环境和多目标控制要求的自学习能力，具有以任意精度逼近任意非线性连续函数的特征。因此可以利用通过神经网络来实现此非线性函数f_k。为此，可以事先计算出大量映射输入、输出关系的开关角样本点，将此样本点交给神经网络学习，通过离线训练，实现此神经网络。该方案将在传统的最优PWM控制的基础上应用神经网络来控制逆变器，改善其性能，提高逆变器的输出电能质量。

1.最优开关角的变化规律

图6-2所示为对六个开关管三相逆变器采用双极性PWM控制的17块脉宽最优PWM波形，该波形在整个周期以及半周期内，分别具有对称性和反对称性，即四分之一波形对称，故有8个开关角。如果三相负载为对称星形联结，则3的倍数次谐波和偶次谐波都为零。将此PWM输出电压波形进行傅里叶级数展开，可得到任一组开关角为θ₁～θ₈的PWM波，逆变器桥臂输出电压的各次谐波有效值V_n为

图6-2 17块脉宽SPWM波形

经过LC低通滤波器后，空载时逆变器输出电压的各次谐波有效值U_n为

U_n＝V_n／［（ω_n／ω₀）2－1］ （6-4）

式中 ω₀——电感L、电容C的谐振角频率，；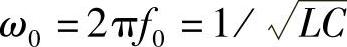

ω_n——各次谐波角频率；

定义r_n为n次谐波电压的传输比，r₁为基波电压传输比，则最优PWM的思想就是：对任一基波电压传输比r₁，都使输出电压总谐波含量最小。

于是式（6-2）就转化为映射

f_k（r₁）＝θ_k （6-5）

空载时逆变器输出电压总谐波畸变率为

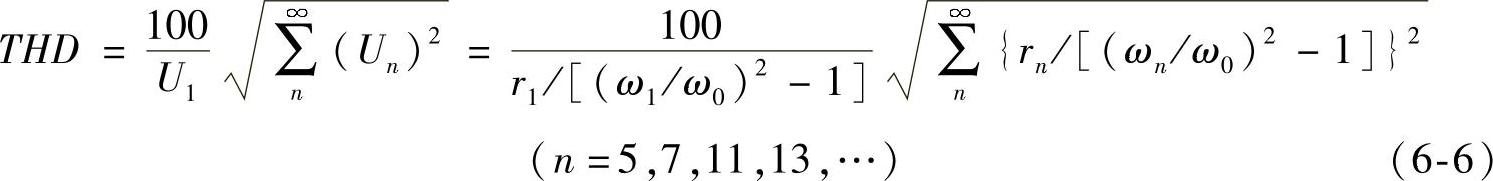
考虑到对于任意特定的r₁，其值是固定的，于是THD最小可以简化为函数y，得(www.xing528.com)

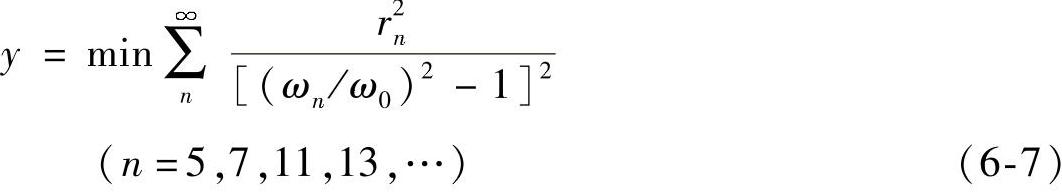
将式（6-3）代入式（6-7），有

此外，输出电压的基波分量

联立解超越方程组式（6-8）、式（6-9）可以得到空载时需要的各开关角θ_k。

需要指出的是，由式（6-8）、式（6-9）求得的开关角θ_k是逆变器空载情况下的最优开关角（见图6-3），根据理论分析和15kVA逆变器滤波参数下最优PWM控制的仿真和负载实验，得出不同负载时的开关角为空载时的0.65。

从图6-3中可以看出，在r₁由0.62～0.85的变化范围中，最优开关角分为连续变化的四个区间：0.62～0.78rad，0.79～0.817rad，0.818～0.832rad，0.833～0.85rad。在各区间交界处开关角阶跃变化，但区间内各开关角的变化是连续的。由图6-4看出，r₁在0.62～0.85的变化范围内，输出电压THD均小于2％，当r₁为0.827时，输出电压THD具有全局最小值0.505。当直流母线电压U_i由280～340V变化，同时负载全范围变化时，该逆变器输出电压谐波畸变率在0.505％～1.788％范围内变化。

图6-3 17块脉宽最优SPWM最优开关角θ₁随r₁变化的关系曲线

图6-4 17块脉宽最优SPWM输出电压最小THD值随r₁变化的规律

2.神经网络拟合仿真分析

根据神经网络理论，假设函数f_k是一条连续光滑的非线性曲线，则根据一定量的映射输入、输出关系的开关角样本点，可以用神经网络根据这些样本点拟合出逼近f_k函数的曲线f_k′函数，并由f_k′计算出其他各种情况下所需要的开关角。

由于三个区间内各开关角跃变较大，且变化趋势各不相同，可以对这三个区段分别用不同的神经网络参数拟合，即所谓分段神经网络法。本方案以0.77422～0.81902区间为对象进行神经网络拟合分析，其他区间完全相似。对各开关角的拟合计算都采用了图6-5所示的单隐含层网络结构。所需的隐含层神经元的个数与被拟合的函数非线性程度相关，神经元个数较多，则拟合精度较好，但计算复杂，耗时较多。根据各开关角随r₁的变化规律综合考虑后，θ₁～θ₄各用2个神经元，θ₅用3个神经元。θ₆～θ₈各用1个神经元。网络各层的计算均采用了误差收敛速度较快的牛顿法及Levenberg-Marquardt^［9］修正算法拟合，整个控制系统如图6-6所示。

图6-5 单输入单输出的单隐含层网络结构图

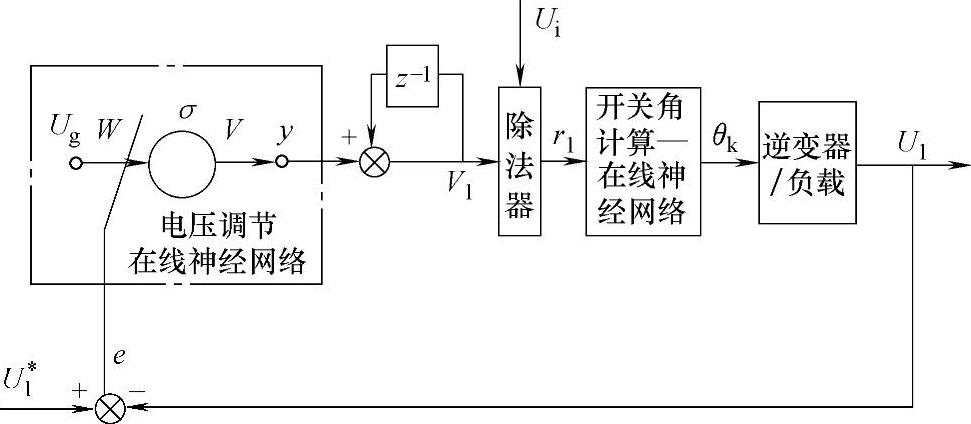
图6-6 输出电压单神经元在线控制原理图

图6-6中点划线框是一种神经元自适应PSD（比例、求和、微分）控制器，根据控制过程误差的几何特性确立性能指标，并建立无需辨识的自适应PSD控制规律。该控制具有良好的动、稳态性能。

U_g为神经元的输入（即网络输入的给定），U₁为系统采样输出电压基波分量，U₁∗为期望的输出电压，σ为神经元激励函数，y为神经元输出，W为输入U_g到神经元的加权系数。

为便于工程实现，简化控制系统的软、硬件结构，隐含层中只用一个神经元，且此神经元的激励函数定义为线性函数。系统采样输出电压基波分量U₁与期望的输出电压U₁∗比较，得到控制过程误差e

e（t）＝U₁^∗（t）－U₁（t） （6-10）以此误差e调节在线神经网络的权值W。定义权值W的调整规则为

W_n＝e_n－1 （6-11）定义输入给定U_g＝1，输出层的权值W＝1，激励函数

f＝σ（U_gW）＝U_gW （6-12）

在系统稳态时，输出电压误差为零，所以调节电压的神经网络输出为零。当系统状态发生变化，例如输入电压和负载变化时，在线神经网络根据输出电压误差e调节权值W，使系统在新的V₁和当前U_i下生成r₁，输入到计算开关角的神经网络，求出相应功率管开关角。

实验证明，该控制方法的系统误差收敛且衰减很快，整个系统稳定，从而改善了逆变器性能，提高逆变器的输出电能质量。