应用遗传算法的神经网络案例分析

应用遗传算法的神经网络的基本原理是用遗传算法（GA）对神经网络的连接权值进行优化学习，利用GA的寻优能力来获取最佳权值。目前已有许多成功的应用，现列举两个例子。

1）求解短期地震预报问题。在改进的MGA中，采用了自适应交叉率和变异率，并且把GA和BP结合起来。预报用三种算法：BP、实数编码遗传算法（GA）、改进型GA（MGA）。图5-10给出了三种方法的比较结果。

图5-10 三种方法的比较

算法参数：网络选用三层BP网络，前一年的最大震级、最大震级之差、累计能量及累计能量之差为网络的输入，网络的输出是下一年的震级，隐含层节点数为30，这个4—30—1网络共有150个可调权值，各层的激发函数均为Sigmoid型函数。BP算法中，学习率η＝0.7；惯性系数α＝0.2。实数GA中，群体容量n＝40，交叉率P_C＝0.12，变异率P_m＝0.1，亲代度量S＝0.9，各参数在算法运行过程中保持不变。MGA中，常量k_c＝0.1，k_m＝0.11。

由实验结果可以看出，遗传算法具有快速学习网络权重的能力，并且能够摆脱局部极小点的困扰。

2）应用于优化基于神经网络结构的控制器的参数。应用神经网络构成一个控制器，用于控制有纯滞后的对象，整个控制系统结构如图5-11所示。

图5-11 控制系统结构

系统采用三层神经网络结构作为控制器，即输入层、隐含层、输出层，根据有关公式与经验，输入层维数n定为2（输入误差e及误差率ec），输出层维数m为1（输出控制量y），隐含层维数n₁定为8。由此构成的神经网络控制器的结构中，共有24个权值需确定。BP网络权值的训练算法中，引用GA作为权值优化方法，根据实际应用情况，选用以下的GA的具体实现形式：

1）由于神经网络的权值为实数，所以解空间采用二进制编码。

2）引入精华策略，即每代都保留父代中几个最优解，以保证搜索过程收敛。

3）引入均匀交叉算子，以求得全局最优解。

其他操作则采用简单的GA的形式。

为了说明神经网络结构的控制和GA参数训练的有效性，选取经典控制问题中较为典型的一阶纯滞后对象进行实验。对象模型为(www.xing528.com)

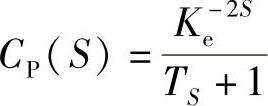
式中，时间常数T＝1，增益系数K＝0.5。采用MATLAB语言编程，分别对系统的定值控制、抗干扰性和鲁棒性进行了仿真实验，结果如图5-12所示。

1）在阶跃输入的情况下，输出响应曲线如图5-12所示。结论：从仿真结果可见，系统动态过程较平稳，超调量小，过渡过程时间短，且静态误差小。说明经过训练后，模糊控制器能达到较好的性能。

2）抗干扰实验：在t＝20时加入单位脉冲干扰信号，仿真结果如图5-13所示。

图5-12 阶跃输入下输出响应曲线

结论：从仿真结果可见，在脉冲干扰作用后，系统能快速、平稳地恢复稳定状态，说明系统抗干扰能力强。

3）鲁棒性实验：改变对象的参数，以检验GA优化后的神经网络控制器的适应性，仿真结果如图5-14所示。

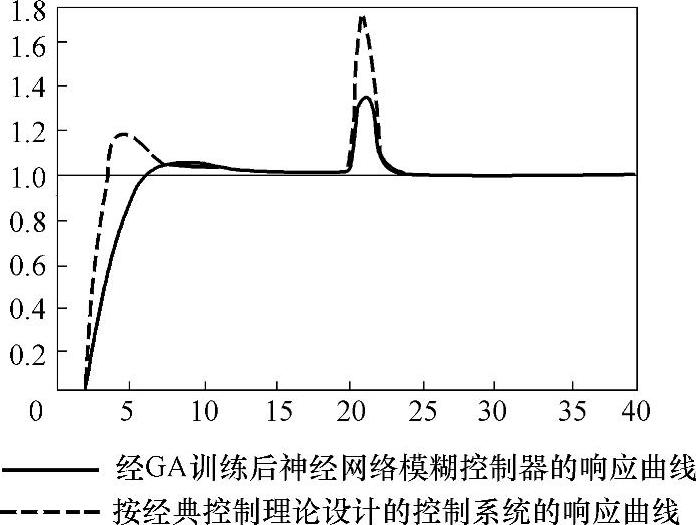
图5-13 单位脉冲干扰信号作用响应曲线

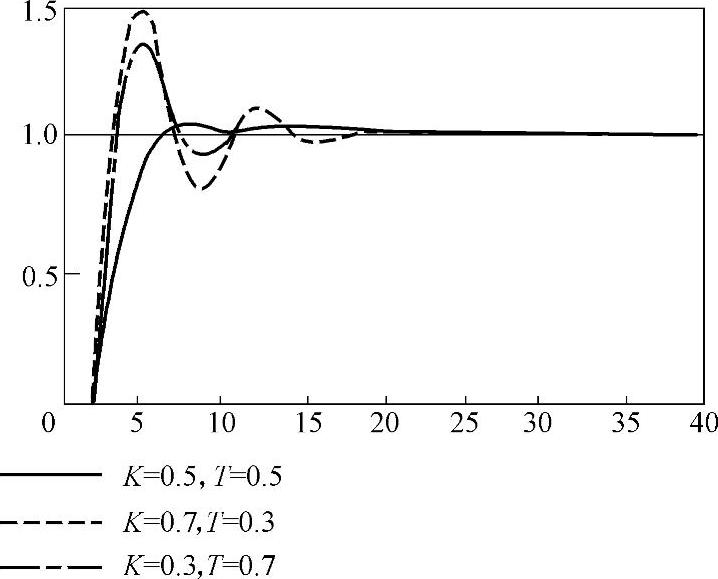
图5-14 K、T变化响应曲线

结论：从仿真结果可见，对象参数改变，对仿真曲线影响不大。说明系统对不同对象适应性强，有较好的鲁棒性。