举例解析5.6遗传算法

用遗传算法求解函数的最大值，即寻找函数f（X）＝X²的最大值，步骤如下：

1.产生初始种群

f（X）＝X²亦即目标函数，X在0～31之间取值，也就是自变量X的一个取值，每一个潜在解（候选解）X代表一个个体，本例个体总数是32。按照产生的原则（一般根据可行性）随机取4个个体构成初始种群，采用5位二进制编码，设为01101、11000、01000、10011，即由这4个个体构成初始种群。

2.选择操作，产生下一代种群

对4个个体逐个解码（将二进制转换为十进制），按目标函数计算适应值。分别为169、576、64、301；它们占总适应值的比例分别是14.4％、49.2％、5.5％、30.9％。采用赌轮选择（见图5-5），如某个体被选中，便得到选择，反之被淘汰。旋转赌轮4次，产生4个个体进入下一代种群。计算被选择数：01101为4×14.4％＝0.576，取整为1，其余分别是11000为2，01000为0，10011为1。01000被淘汰，新下一代为01101、11000、11000、10011。

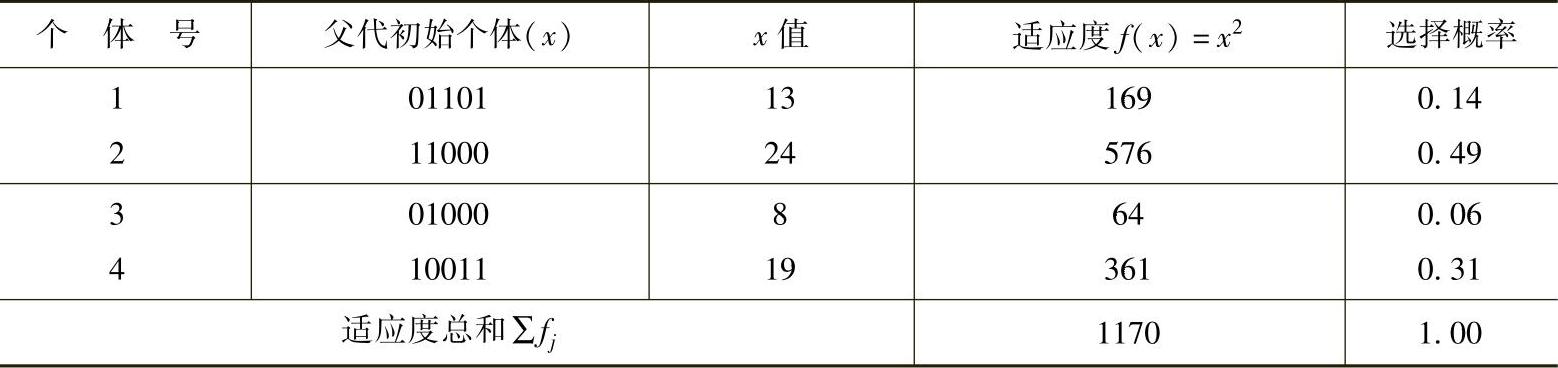
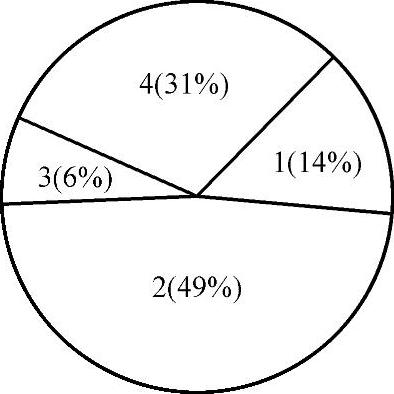
图5-5 赌轮选择

计算出群体中各个个体的选择概率后，为了选择交配个体，需要进行多轮选择。每一轮产生一个［0，1］之间均匀随机数，将该随机数作为选择指针来确定被选个体。个体被选后，可随机地组成交配对，以供后面的交叉操作。

3.交叉操作

5位二进制字符串构成的间隙位置k为1～4，若C₁＝11000与C₂＝10011相交于k＝4，交叉产生新的个体就是C₁′＝11001和C₂′＝10010。设4个新下一代个体两两相配，随机选取个体1与个体2相配k＝4，个体3与个体4相配k＝2，得出的结果是优势互补。通过交叉操作，种群的总适应值和平均适应值都得到改善，见表5-1。(www.xing528.com)

表5-1 选择操作后前后的各项数据

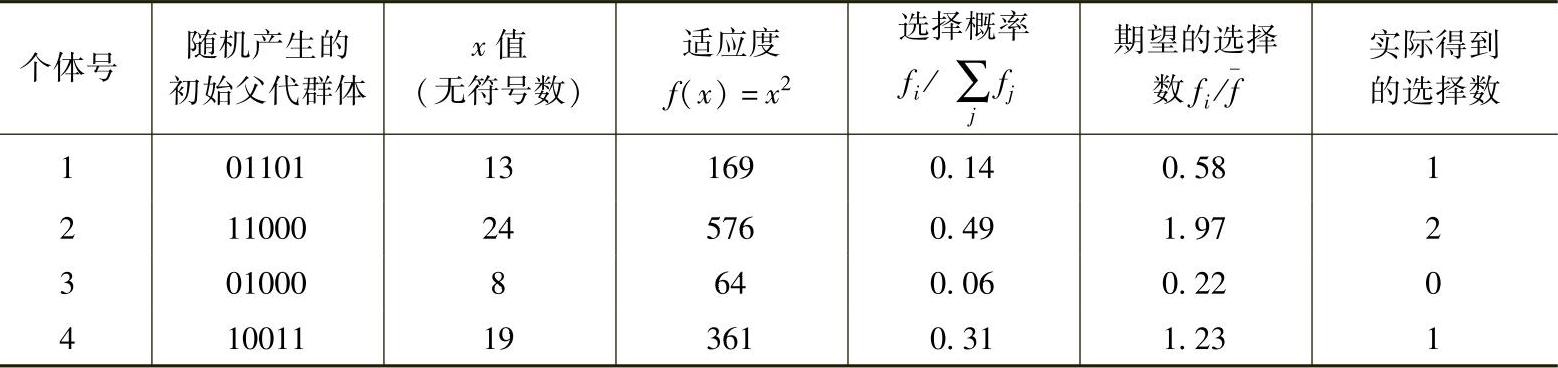
4.变异操作

对于二进制变异操作就是随机选取位进行0→1，或为1→0的操作。变异的概率非常小，经典取值为0.001～0.01。对于本例种群共有4×5位＝20位，若概率取0.001，变异的位数是20×0.001位＝0.02位，若概率取0.05，变异的位数是20×0.05位＝1位。由于位置随机选取，如果位置刚好就是交叉后的新种群的第3位，那么个体11011→11111，至此得到变异后新的种群。

重复1～4的操作，直到循环次数到达预定次数，得到最后的种群，即得到最优解或本题的最大值。其流程如图5-6所示。

最大适应值从729变成31×31＝961这是我们所希望的。

5.终止条件

经过三个遗传算子操作之后，当找到一个合适的解最大值或到达预先设定的计算时间，则计算停止，否则重复2～4步，如此循环往复。对于本例，如得到最优个体11111，算法便告终止。

从上例得当到经过一个循环选择、交叉和变异操作后，种群的最优适应度和平均适应值都得到提高，表明每一次遗传操作，都使问题的解向前前进一步；随着种群一代一代地不断进化，最终将获得全局最优解。