学习规则-探析BP算法的输入输出映射实现

BP算法采用学习规则是通过使代价函数最小化的过程来完成输入到输出的映射。通过负梯度搜索技术，使网络的实际输出值的误差二次方和为最小。这种方法与其等价的一般化误差比较，可以减小运算量。

1.计算过程

BP算法分成两个阶段：

第一阶段：正向传播。

在正向传播过程中，输入信息从输入层经隐含层逐层处理，并传向输出层，获得各个单元的实际输出，每一层神经元的状态只影响下一层神经元的状态。

第二阶段：反向传播。

如果在输出层未能得到期望的输出，则转入反向传播进行反向计算，由梯度下降法调整各层节点的权值和阈值，计算出输出层各单元的一般化误差，然后将这些误差信号沿原来的连接通路返回，以获得调整各连接权所需的各单元参考误差，通过修改各层神经元的权值，使得误差信号最小。

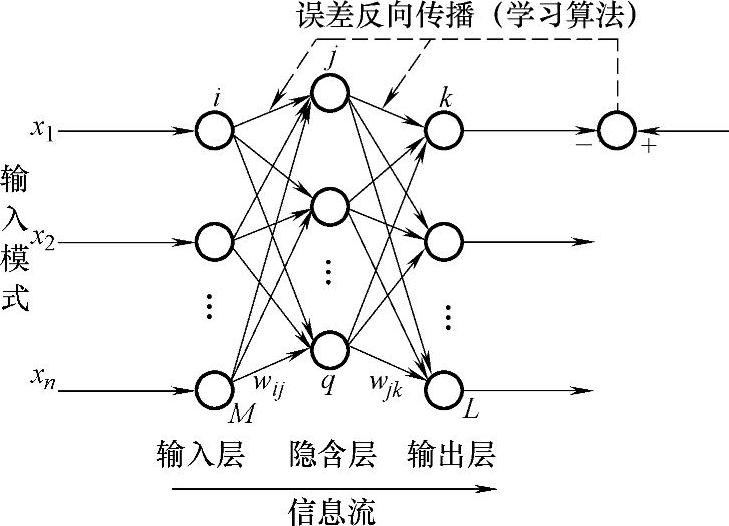
图4-12 BP型神经网络拓扑结构

（1）正向传播阶段

训练过程开始，设置输入向量、理想输出向量、权值初始化。在训练该网络的学习阶段，设有N个训练样本，先假定用其中的某一个固定样本中的输入模式X和d_pk对网络进行训练（d为期望输出符号）。为书写方便，暂时将公式中样本p的记号略去，如对隐含层中的第j个节点的输入写为

式中 M——输入层节点数。

隐含层中第j个节点的输出为

O_j＝f（net _j） （4-10）

式中 f（net_j）——激活函数

f（net_j）＝1／（1＋exp（－net）） （4-11）

第j个节点的输出O_j，将通过加权w_ij向前传播新第k个节点，输出层第k个节点的总输入为

式中 q——隐含层节点数，输出层第k个节点实际网络输出

O_k＝f（net_k） （4-13）

上述正向传播学习训练，是从输入层到输出层进行计算，当学习样本输入网络后，就会产生一组输出，将该输出与目标输出相比较，便得到误差，视误差大小，决定是否结束或转入反向传播计算。

定义网络输出误差函数为

系统的平均误差函数为

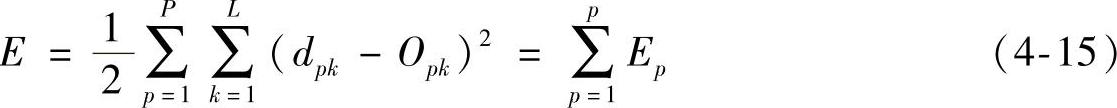
式中 p——样本模式对；

L——网络输出节点数。

为了简化计算，略去p，则有

（2）反向传播计算

如果前向计算误差大于目标值，则要进行反向传播计算，即要逆着正向信号方向从输出层到输入层进行计算，主要是对权值和阈值进行调整，即将权值按E函数梯度变化的反方向进行调整，使网络输出接近期望值。

1）输出层权系数的调整：权值的修正公式为

式中 η——学习速率，η＞0。

定义反向传播误差信号δ_k为

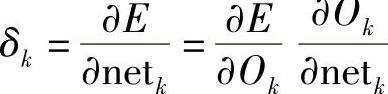
式中

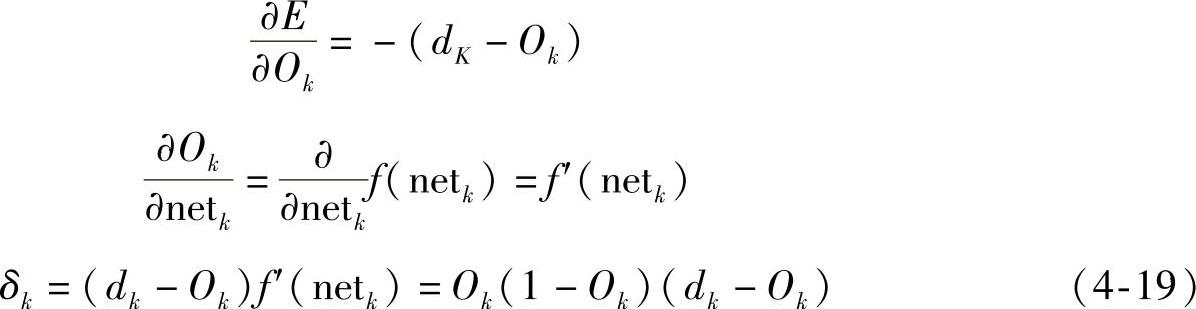
又

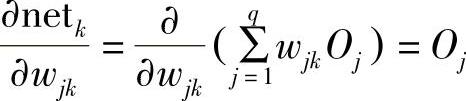
由此可得输出层的任意神经元权系数的修正公式为

Δw_jk＝η（d_k－O_k）f′（net_k）O_j＝ηδ_kO_j （4-20）经过推导，可得输出层的任意神经元权系数的修正公式为

Δw_jk＝ηO_k（1－O_k）（d_k－O_k）O_j （4-21）

2）隐含层权系数的调整：权系数的变化量为

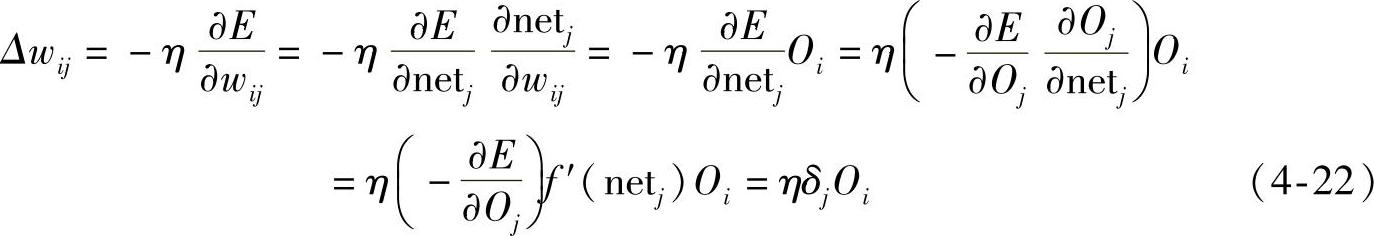
式中，（∂E／∂O_i）不能直接计算，需通过其他间接量进行计算，即

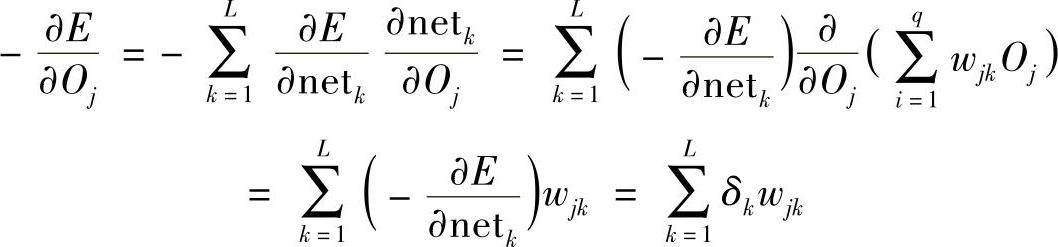
显然有

3）网络连接权值调整式：将样本标记p记入公式后，对于输出节点k有：

Δ_pw_jk＝ηf′（net_pk）（d_pk－O_pk）O_pj＝ηO_pk（d_pk－O_pk）O_pj （4-24）

对于隐含层节点j有

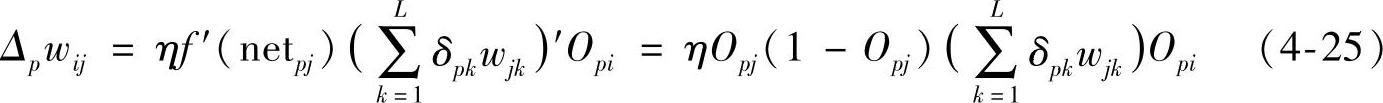
根据以上推导，可得网络连接权值调整式为

w_jk（t＋1）＝w_ij（t）＋ηδ_iO_i＋α［w_ij（t）－w_ij（t－1）］ （4-26）

式中 t＋1——第t＋1步；

α——平滑因子，0＜α＜1。

当网络输出值与期望值d_k不一致时，则将其误差信号从输出端反向传播，进行向后传播计算，直到误差满足要求为止。

（3）BP学习算法的计算步骤(www.xing528.com)

1）初始化，置所有权值为较小的随机数。

2）提供训练集

设第p组样本输入u_p＝（u_1p，u_2p，…，u_np）

输出d_p＝（d_1p，d_2p，…，d_np）

3）计算实际输出，计算隐含层、输出层各神经元输出。

4）计算目标值与实际输出的误差E，用式（4-14）。

5）若偏差满足要求，计算结束，否则反向传播计算，直到误差满足要求为止。

算法程序框图如图4-13所示。

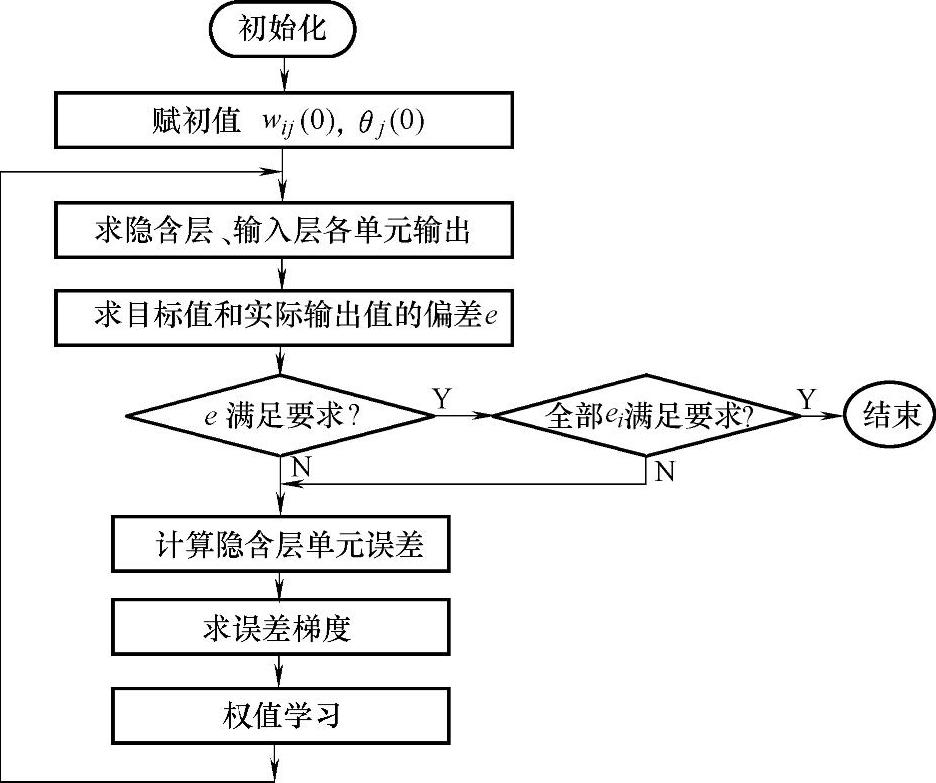
图4-13 算法程序框图

2.注意事项、存在问题与改进

（1）注意事项

BP型神经网络有多种用途，在使用BP算法时，应注意的几个问题是：

1）学习开始时，各隐含层连接权系数的初值应以设置较小的随机数为宜。

2）采用S型激活函数时，由于输出层各神经元的输出只能趋于1或0，不能达到1或0。在设置各训练样本时，期望的输出分量d_pk不能设置为1或0，以设置为0或1较为适宜。

3）学习速率η的选择，在学习开始阶段，η选较大的值可以加快学习速度。学习接近优化区时，η值必须相当小，否则权系数将产生振荡而不收敛。平滑因子α的选值为0＜α＜1。

（2）存在的问题

1）收敛速度相对较慢。

2）局部极小点有待进一步探索。

3）网络瘫痪问题。

在训练中，权值可能变得很大，这会使神经元的网络输入变得很大，从而又使得其激活函数的导函数在此点上的取值很小。根据相应式子，此时的训练步长会变得非常小，进而将导致训练速度降得非常低，最终导致网络停止收敛。

4）难以确定隐含层和隐含层节点数目。

（3）算法的改进

1）采用动态步长。

2）与其他全局搜索算法相结合。

3）模拟退火算法（退火算法见下面叙述）。

3.BP神经网络的设计

（1）输入、输出层的设计

输入层的设计可以根据需要求解的问题和数据表示方式确定，若输入信号为模拟波形，那么输入层可以根据波形的采样点数目决定输入单元的维数，也可以用一个单元输入，这是输入样本为采样的时间序列。输出层的维数可以根据使用者的要求确定。如果BP神经网络用作分类器，类别模式一共有m个，那么输出层神经元的个数为m。

（2）隐含层的设计

隐含层单元的数目与问题的要求、输入／输出单元的数目都有直接的关系，隐含层单元的数目太多，会导致学习时间过长、误差不一定最佳，也会导致容错性差、不能识别以前没有的样本等，因此，一定存在一个最佳的隐含层单元数，通常用以下三个公式来选择最佳隐含层单元数：

① 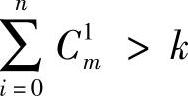，其中k为样本数，n为输入单元数。

② 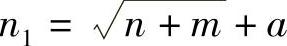，其中m为输出神经元数，n为输入单元数，a为［1，10］之间的常数。

③ n＝log₂n，其中n为输入单元数。

（3）初始权值的选取

如果各个初始权值都一样，可能对训练不利，所以一般要求取足够小的随机数，以避免训练从饱和区域开始而影响收敛。下面不加证明地介绍适合于单个隐含层的Nguyen和Widrow的权值初始化算法：

设n₀为输出层的神经元个数，n₁为隐含层的神经元个数，而λ为比例因子，于是

① 计算比例因子。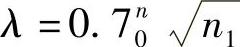

② 将各权值初始化为－0.5～0.5的随机数。

③ 对各权值再次初始化

④ 对于隐含层中的第i个神经元，将其阈值初始化为－w_ij与w_ij之间的随机数。4.前馈型神经网络设计中应注意的问题

一般情况下，神经网络输入和输出神经元的个数与实际的输入输出变量个数相等，于是，前馈型神经网络的结构就取决于隐含层的层数、每个隐含层所包含的神经元个数以及各神经元激活函数的形式。

Hornik等证明，具有足够多隐含神经元的单隐含层MLP能够逼近任意Borel可测函数，因此可以用作非线性函数的通用逼近器。在这里，“足够多”的定义太模糊，实际上很难具体确定。所以，隐含单元的个数通常通过试凑方式确定。对于比较复杂的非线性逼近问题，通常采用两层隐含单元的网络结构。

一般来说，隐含单元的个数越多，神经网络的非线性逼近能力或学习能力就越强，但是这个结论不是绝对的。如果用于训练的样本集能够充分反映实际的输入输出特点，也就是说，实际系统的所有特征全部反映在训练样本中，那么以上结论成立。但是如果样本集不能反映实际系统的全部特征，甚至有所遗漏或“误导”，那么已训练的神经网络可能出现与训练样本完全吻合，但对未训练过情况出现较明显误差的情况，于是表现为较弱的“泛化（Generalixation）”能力，这就是所谓的对训练样本的“过分吻合（Overfit）”现象。

5.应用示例：车床切削加工切削用量的选择^［7］

金属切削加工中，切削用量的选择受到多种因素的影响，其变化与组合众多，运用神经网络非线性映射能力，恰当选取影响切削用量选择的特征因素，建立切削用量和各影响因素之间的神经网络映射模型，运用机床过去运行数据进行训练，自动寻找规律，并分布储存于权值中，运行时，对输入切削条件参数通过计算求解出最佳切削用量。

网络结构采用BP神经网络，如图4-12所示，输入为影响切削用量选定的因素，包括加工方法、工件、刀具、切削液、机床及生产目标等特征因素，粗加工14项、精加工13项，以此作为输入层节点数。切削用量为输出，切削用量主要参数为切削速度、进给量和加工深度，由于加工深度一般为固定，故只取前两项作为输出层节点数，即y＝2。隐含层节点数在训练中确定。

对输入参数和输出参数要进行归一化处理，归一化函数为

Z_iu＝0.9（Z_i－Z_min）／（Z_max－Z_min）＋0.05

式中 Z_i，Z_iu——某一切削条件参数或切削用量参数及其规一化值。

Z_max＝max｛Z_i｝，Z_min＝min｛Z_i｝；i＝1，2，…，k

由于网络的输出是归一化了的切削速度和进给量，因而在模型工作过程中，对网络输出进行了反归一化换算：

Z_i＝（Z_iu－0.05）（Z_max－Z_min）／0.9＋Z_min

对于连续的特征向量，如工件材料硬度和强度、刀具材料的硬度和抗弯强度等，可直接运用归一化公式；而对于非连续的输入特征向量，则要首先对其进行编码、量化，然后再对编码值进行归一化处理。

用从实践经验中取得的样本数据集（输入、输出）对网络进行训练，以获得有效的网络工作模型。模型进行工作时，切削条件参数向量由输入层通过权值和作用函数传播到隐含层，再由隐含层通过权值和激活函数传播到输出层，在输出层求出切削速度和进给量。按照上述算法程序及图4-13，训练开始进行初始化，设置权初始值随机取一个小于1的数值，取初始阈值等于1。对每一个样本，按式（4-17）～式（4-21）进行计算隐含层及输出层输出值，激活函数，用式（4-11）。然后按式（4-14）计算与目标值的偏差。观察是否满足需要，即最小，若不符要求，则反向传播计算，直到满是要求为止。在网络的训练过程中，按式（4-24）和式（4-25）不断改变权值，修改隐含层节点数目，学习步长加快收敛，最终找到能够满足收敛精度要求的最小规模网络，得到粗、精加工切削用量网络参数见表4-1，从而可建立神经网络模型。

表4-1 粗加工与精加工神经网络模型参数表

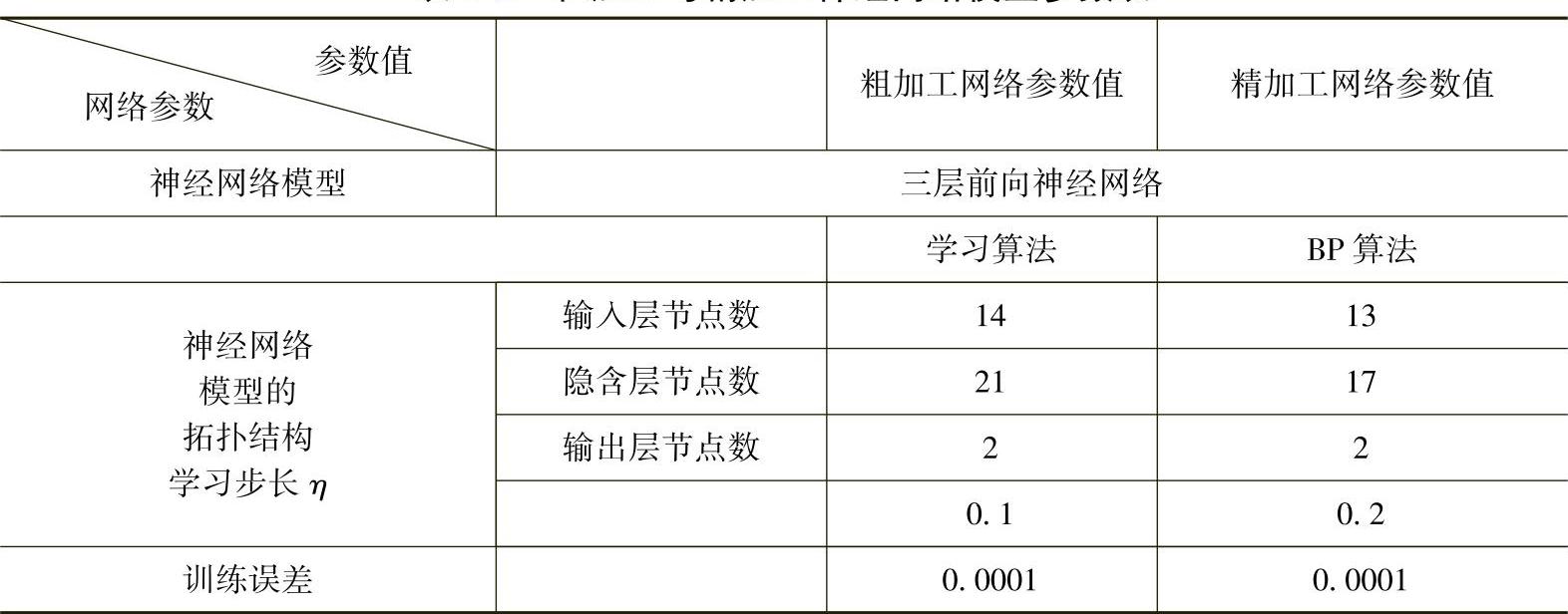
在神经网络模型建立的基础上，可以开发车削加工智能化最佳用量选择软件。现在CA6140车床上加工45＃钢，毛坯为直径ϕ60mm的棒料，无外皮，外圆纵车，采用YT15可转位刀片，刀具前角：12°，主偏角：45°，刀杆尺寸：16mm×25mm，刀具寿命：60min，粗加工切削深度：2mm，精加工切削深度：0.5mm，加工表面完工粗糙度R_a＝3.2mm。将各切削条件输入软件中，得到输出粗加工切削速度：120m／min，进给量：0.6mm／r，精加工切削速度：180m／min，进给量：0.4m／r。采用所选用量进行加工，完全达到加工要求。