学习算法的区别感知器与多层感知器学习算法差异

1.学习算法

感知器引入的学习算法称为误差学习算法，其步骤如下：

1）选择一组初始权值w_i（0），可以是随机的较小的非零值。

2）计算与某一输入模式对应的实际输出与期望输出的误差δ。

3）如果δ小于给定值，结束；否则继续。

4）更新权值（阈值可视为输入恒为1的一个权值）：

Δw_i（t＋1）＝w_i（t＋1）－w_i（t）＝η［d－y（t）］x_i （4-5）

式中 t——计算操作步数；

η——在区间（0，1）上的一个常数，称为学习步长，它的取值与训练速度

和w收敛的稳定性有关；

d、y——神经元的期望输出和实际输出，即δ＝d—y（t）；

x_i——神经元的第i个输入。

5）返回2），重复，直到对所有训练样本模式，网络输出均能满足期望值。

这个学习过程就类似于一个闭环反馈过程。学习过程的稳定性取决于学习率η的选择：小的学习率可以使得系统收敛于一个稳定的解；大的学习率可以加速学习的过程。

感知器学习算法称为误（偏）差学习算法，可用于模式识别，不宜用于多层前馈神经网络和后述的BP神经网络。

2.多层感知器（MLP）

（1）多层感知器的组成(www.xing528.com)

MLP采用监督学习，其原理结构如图4-11所示。这是一个完全连接的前馈神经网络，由输入层、隐含层和输出层组成。其中，隐含层可以有多个，图中所示为两个隐含层。每一层包含多个神经元，输入层的神经元个数为n₀个，第1隐含层神经元个数为n₁个，第2隐含层神经元个数为n₂个，输出层神经元个数为n₃个，每个神经元的结构完全一样。

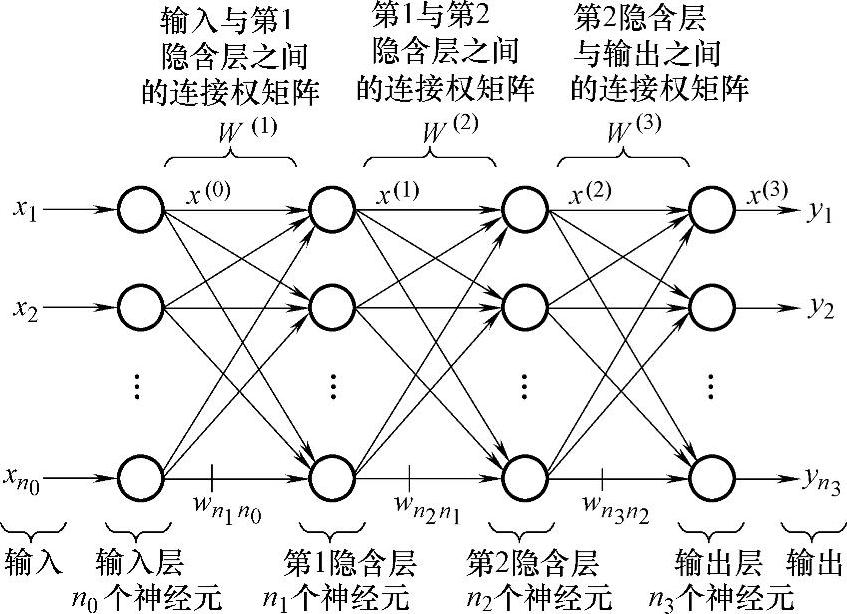
图4-11 多层感知器结构示意图

第1隐含层与输入层之间的连接权矩阵是W（1），于是

第1隐含层与第2隐含层之间的连接权矩阵是W（2），于是

隐含层的层数可以有多个，为简便计，这里只考虑两层。

输出层包含n₃个神经元，它们与第2隐含层的各个神经元呈完全连接状态，所以与输入层之间形成n₃n₂个连接权矩阵W^（3），它们的输出是x^（3）。

输出层的活化函数可以取多种形式，常用线性函数和Sigmoid函数，对于函数逼近问题，多采用线性函数。

（2）多层感知器的结构特点

多层感知器是全局性前馈型神经网络的典型代表。根据连接权对网络输出的影响，可以把前馈型网络分成全局性网络和局部性网络两种，它们反映着不同的设计思想。作为全局性前馈型神经网络的典型代表，多层感知器具有以下特点：

1）同一层神经元之间没有任何连接，各个神经元自身也不存在连接。

2）相邻的两层神经元之间呈完全连接，即其中一层的每一个神经元与另一层的每一个神经元之间都存在连接权，但是隔层之间不存在直接连接。

3）信息传递是有方向性的。前向计算时，由于根据输入来计算网络的实际输出，只能按图4-11所示的箭头方向进行，即先计算第1隐含层的输出，然后计算第2隐含层的输出，最后计算输出层的输出，而下面所讲的误差反向传播以修正各连接权时，则完全反方向进行。