模糊关系与模糊矩阵分析

（1）模糊关系

如果模糊控制规则只有一条，推理就很简单了。实际上规则是多条的，前提部和结论部都不止一个，都可构成子集，而且子集中的元素互有关系，这时就要找出一个综合的前提部子集，这就是模糊关系，如图3-10中的R，利用它进行推理求出结论，如图3-10中的C。模糊关系是指多个模糊集合的元素间所具有关系的程度。

模糊关系的定义为：设X，Y是两个非空集合，则X×Y的一个模糊子集R称为X到Y的一个模糊关系，X×Y是笛卡儿乘积，R称为模糊关系；其特性为

μ_R：X×Y→［0，1］

（2）模糊矩阵

模糊关系可用模糊矩阵表示，可使我们进一步了解模糊关系的意义，下面举一个例子。

设有7种物品：苹果、乒乓球、书、篮球、花、桃和菱形图案组成一个论域，并且以x₁，x₂，x₃，…，x₇分别为这些物品的代号，则论域U＝｛x₁，x₂，x₃，x₄，x₅，x₆，x₇｝，因此物品两两相似的程度R可列为表3-3，它是从U到U′的一个模糊关系。

表3-3 物品两两相似程度的模糊关系

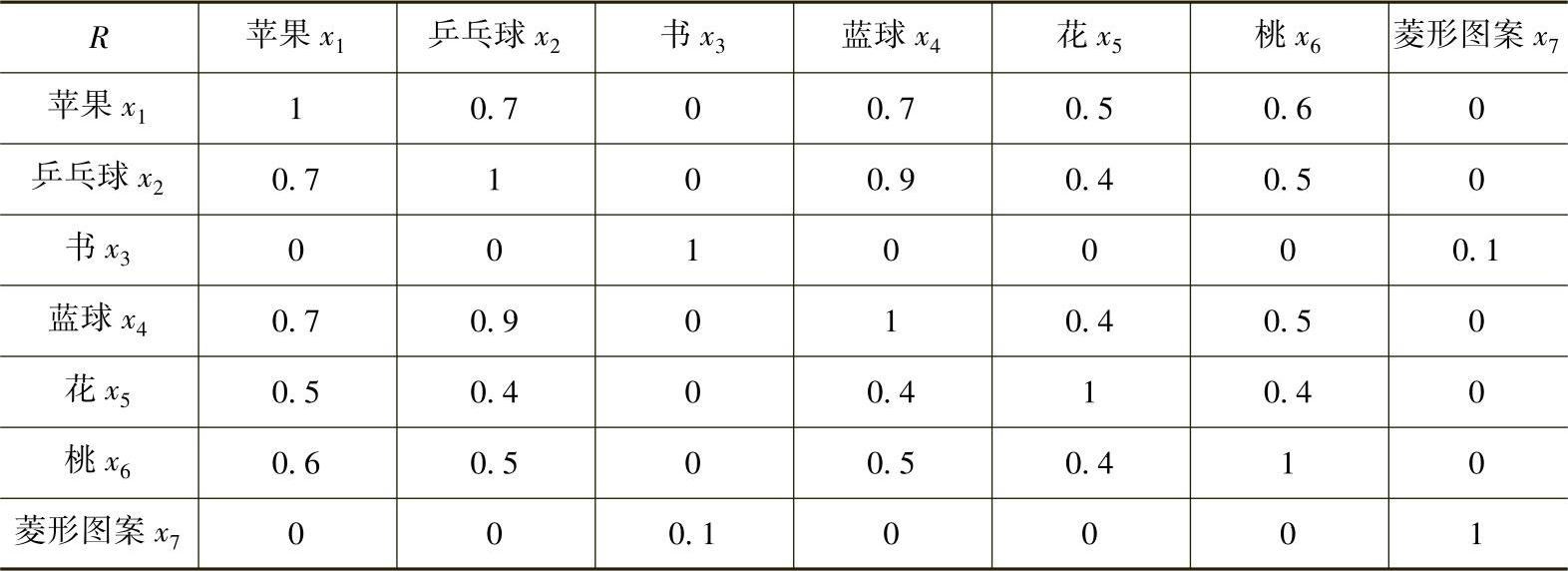
用模糊矩阵表示上述模糊关系时，可写为

（3）矩阵的运算

设有n阶模糊矩阵A和B，A＝（a_ij），B＝（b_ij），且i，j＝1，2，…，n，则定义如下几种模糊矩阵的运算方式：

1）相等

若a_ij＝b_ij，则A＝B （3-18）

2）包含

若a_ij≤b_ij，则A∈B

3）并运算

若c_ij＝a_ij∪b_ij，则C＝（c_ij）为A和B的并集，记为C＝A∪B （3-19）

4）交运算

若c_ij＝a_ij∩b_ij，则C＝（c_ij）为A和B的交集，记为C＝A∩B （3-20）(www.xing528.com)

5）补运算

若c_ij＝1－a_ij则C＝（c_ij）为A的补集，记为C＝A （3-21）

（4）模糊关系与模糊矩阵的合成

模糊矩阵合成是指：根据第一个集合和第二个集合之间的模糊关系与第二个集合和第三个集合之间的模糊关系，进而得到第一个集合和第三个集合之间模糊关系的一种运算形式。模糊矩阵的合成类似于普通矩阵的乘积，将乘积运算换成“取小”，将加运算换成“取大”即可。

设矩阵A是x×y上的模糊关系，矩阵B是y×z上的模糊关系，则C＝A▫B称为A与B矩阵的合成。合成算法为

C_ij＝｛A_ij▫B_ij｝

表示合成运算。

例：c_ij＝｛a_ik▫b_kj｝ （3-22）

或

c_ij＝∨｛a_ik∧b_kj｝

式中 k——维数。

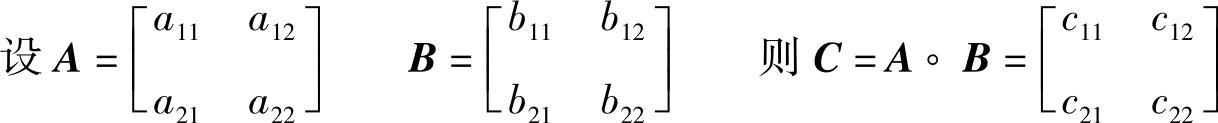
式中

C₁₁＝（a₁₁∧b₁₁）∨（a₁₂∧b₂₁）

C₁₂＝（a₁₁∧b₁₂）∨（a₁₂∧b₂₂）

C₂₁＝（a₂₁∧b₁₁）∨（a₂₂∧b₂₁）

C₂₂＝（a₂₁∧b₁₂）∨（a₂₂∧b₂₂）

∨取最大值计算，∧取最小值计算。