传统的一般集合:A={X1,X2,X3,X4,…}或A={X|X是正整数离散值},X是构成集合的元素或子集。
设集合A由0~1之间的连续实数组成,即
A={X,X∈R,0≤X≤1.0}
上述的集合是不模糊的,对任意元素X只有两种可能,属于A和不属于A,这种特性可以用特征函数CA(X)来描述,即

在模糊集合中,为了表示模糊概念,要应用隶属函数及隶属度的概念,隶属函
数相当于传统集合的特征函数,它的定义为

式中 μA(X)——模糊集合的隶属函数;
A——模糊集合,常表示为A=(X,u)。
u为论域范围[0,1],即控制过程参数变化的范围,模糊控制器输入量的实际范围称为基本论域。
设给定论域u,u到[0,1]闭区间的任一映射
μA:u→[0,1]
u→μA(X)
都确定u的一个模糊子集A,μA(X)称为模糊子集的隶属函数,μA(Xi)称Xi对于A的隶属度,也可记为A(Xi),Xi是u中一个取值元素,应注意μA(X)和μA(Xi)的区别。
模糊集合的表达方式:
1.当u为离散有限集{χ1,χ2,…,χn}时,
(1)Zadeh表示法
A=μA(X1)/X1+μA(X2)/X2+…+μA(Xn)/Xn (3-1)
式中,/表示对应关系;+表示整体。
例:如A={1、2、3、4、5、6、7、8、9、10}表示为
A=0/1+0/2+0.3/3+0.7/4+1/5+1/6+0.7/7+0.3/8+0/9+0/10
A的0/Xj的元素称为台,其值为零,故上式可写为
A=0.3/3+0.7/4+1/5+1/6+0.7/7+0.3/8
(2)序偶表示法
将论域中的元素uj与其隶属函数A(u)构成序偶来表示A,称为序偶表示法。
A={(X1,μA(X1)),((X2,μA(X2)),…,(Xn,μA(Xn))}(3-2)
上例可表示为
A={(1,0),(2,0),(3,0.3),(4,0.7),(5,1),(6,1),(7,0.7),(8,0.3),(9,0),(10,0)}
也可除去为零的项
A={(3,0.3),(4,0.7),(5,1),(6,1),(7,0.7),(8,0.3)}
(3)向量表示法
A={μA(X1),μA(X2),…,μA(Xn)}(3-3)上例表示为(https://www.xing528.com)
A={0,0,0.3,0.7,1,1,0.7,0.3,0,0}
2.当U是有限连续域时,记为

∫不是表示积分,μA(X)/X是上下两者的关系。
隶属函数的值域为0~1闭区间连续取值,函数μA(Xi)越接近1,表示元素Xi属于模糊集合A的程度越大;反之,μA(Xi)越接近于0,表示元素Xi属于模糊集合A的程度越小。应注意的是,模糊集合和几率的值域均是[0,1],但两者不可混淆。
“高”是一个模糊概念,“身高”是一个可以度量的客观物理精确量。两者之间有一个隶属度,例如:
μ(高)={(150,0.0),(160,0.0),(165,0.25),
(170,0.5),(180,1.0),(200,1.0)}
小括号中第一个数为身高,第二个数是隶属度。它表示150cm和160cm的人均不能称之为“高“(隶属度为0.0);180cm,200cm绝对可以称之为“高”(隶属度为1.0);而身高165cm和170cm的人属于“高”的程度,分别为0.25和0.5。此一概念可进一步用图3-2表述。横轴为身高(精确量),纵轴是各身高高度对此一模糊概念的“隶属度”,其值由0到1。据此,我们可以定义出“高”的“隶属函数”如图3-2所示,附有矮的隶属函数。

隶属函数可以看成是精确量和模糊量之间的一种转换关系。
如何决定隶属函数是一个重要的基本课题,常用方法有:①模糊统计法;②例证法;③专家经验法等。决定隶属函数与经验有关,一般做法为,首先确定一个适宜的最大的隶属函数点,然后向两侧延伸,要求是单调递减,不允许有波浪形。隶属函数要求是单峰馒头形,不能有两个最大值,即所谓凸模糊集合。模糊控制理论发展之初,大都采用吊钟形的隶属函数,但近几年为了简便,几乎都已改用三角形的隶属函数,这是由于三角形计算上比较简单,且在性能上与吊钟形几乎没有差别的缘故,常用的隶属函数还有梯形。图3-3为三角形、梯形隶属函数。图3-3a为三角形,图3-3b为梯形。

图3-2 身高的隶属函数

图3-3 三角形、梯形隶属函数和模糊单点
a)三角形 b)梯形 c)模糊单点
三角形隶属函数 其形状由三个参数a、b、c确定

a、c是脚,b是顶峰
梯形隶属函数 其形状由4个参数a、b、c、d确定

a、d是脚,b、c是两肩。
若输入值x0是精确的,则将其模糊化为模糊单点A,如图3-3c所示,即

语言(模糊)变量有数个模糊值时,可分别以隶属度对应到绝对量。如图3-4所示,模糊变量“危险度”有高、中、低三个模糊值。每一模糊值又与(火灾)发生频率值有不同的隶属度。当具体应用时,如对于不同范围的输入值,隶属函数应分为偏小型函数、偏大型函数和中间对称型函数,如图3-5所示。
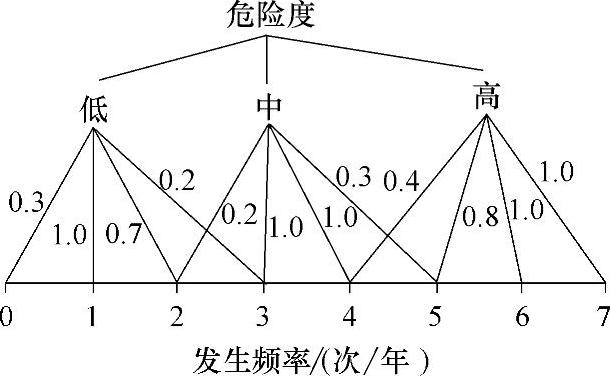
图3-4 三个模糊值的隶属函数

图3-5 不同范围隶属函数典型分布
a)偏小型函数 b)偏大型函数 c)中间对称型函数
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




