名词解释：附录六

1.庞加莱（Poincar）截面

一个非线性动力系统在相空间上的相轨迹被一个面所截，这个面就可以叫做庞加莱截面。

在多维相空间（x，dx／dt，x_Z，dx_z／dt，…，x_n，dz_n／dt）中，适当选取一截面，在此截面上，某一对共扼变量如x₁-dx₁ dt取固定值，称此截面为庞加莱截面。

2.相空间

相空间是庞加莱提出来的。

相空间是动力学系统中坐标是状态变量或状态向量的分量组成的空间。

相空间是数学与物理学概念，是一个用以表示出一系统所有可能状态的空间；系统每个可能的状态都有一相对应的相空间的点。相空间是一个六维假想空间，其中动量和空间各占三维。每个相格投影到px-x平面上后面积总是h。尽管相格的形状如图2-6所示，可能十分任意，但我们可以把它们想象为方形的或长方形的。

3.非线性动力学系统

动力学是理论力学的一个分支学科，原来主要是研究作用于物体的力与物体运动的关系，现在动力学系统的研究领域已经扩大，例如增加热和电等成为系统动力学；增加生命系统的活动成为生物动力学等，这都使得动力学在深度和广度两个方面有了进一步的发展。那些研究非线性动力学的系统就是非线性动力学系统。非线性动力学系统主要包括混沌、分岔、孤立子三个方面。

4.非奇异吸引子

动力学系统从某个初始点出发，最终围绕相空间中某个明确的形状游荡。例如，曲线可以向一个闭合环旋进后，绕环永远兜圈子，而且初始条件的不同选择会导致相同的终末形状。倘若如此，那形状就叫做吸引子。

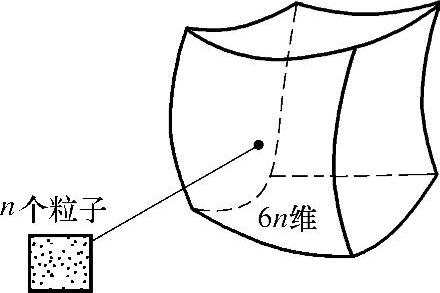
图2-6 相空间

吸引子是一个数学概念，描写趋向于定态的系统运动的收敛类型。一类是指相空间有一个点集S或一个子空间，对S邻域任一点当t时，所有的轨迹都趋于S。吸引子是一个稳定的不动点。例如有阻尼的单摆运动，最终要停在一个固定点上，此点像磁石一样吸引摆锤，就是不动点—形象地称此点为吸引子，这是一类最简单的吸引子。第二类吸引子是极限闭环，它描述趋向于周期性地重复同样行为的系统在状态空间的稳定振荡。第三类混吸引子是环面吸引子，它描述复合振荡的周期行为，它的轨道绕行在状态空间的一个环面上。这三类吸引子合称为非奇异吸引子或非混沌吸引子，如图2-7a、b、c所示。

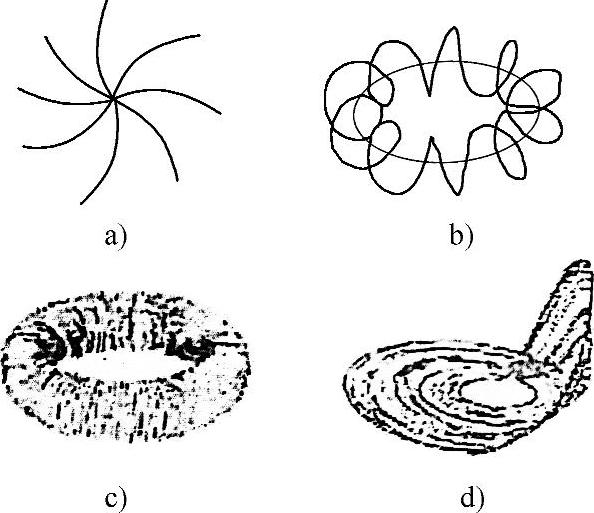
图2-7 动力学系统各种吸引子(www.xing528.com)

a）定常吸引子 b）周期吸引子 c）准周期吸引子 d）混沌吸引子

5.奇异吸引子

非线性振子有稳定的极限环解，称为一维吸引子。一个体积的维数是一个正整数，例如，零、一、二、三，合称为整数维吸引子。也有分数维数存在，例如，大气流体力学发现三维空间混沌解，其维数在二～三之间，股市混沌的维数在一～三之间。这种分数维数的吸引子叫奇异吸引子或混沌吸引子，是对应于混沌运动的物理过程的一个抽象数学概念。在观察上，整数维数的吸引子有光滑的周期运动解，分数维分数的吸引子有非光滑的复杂周期解或者简称为混沌解。奇异吸引子是相空间中具有分数维数的吸引子集合，混沌轨道运行在该集合中，它具有复杂的拉伸、折叠和伸缩结构。混沌吸引子如图2-8所示。

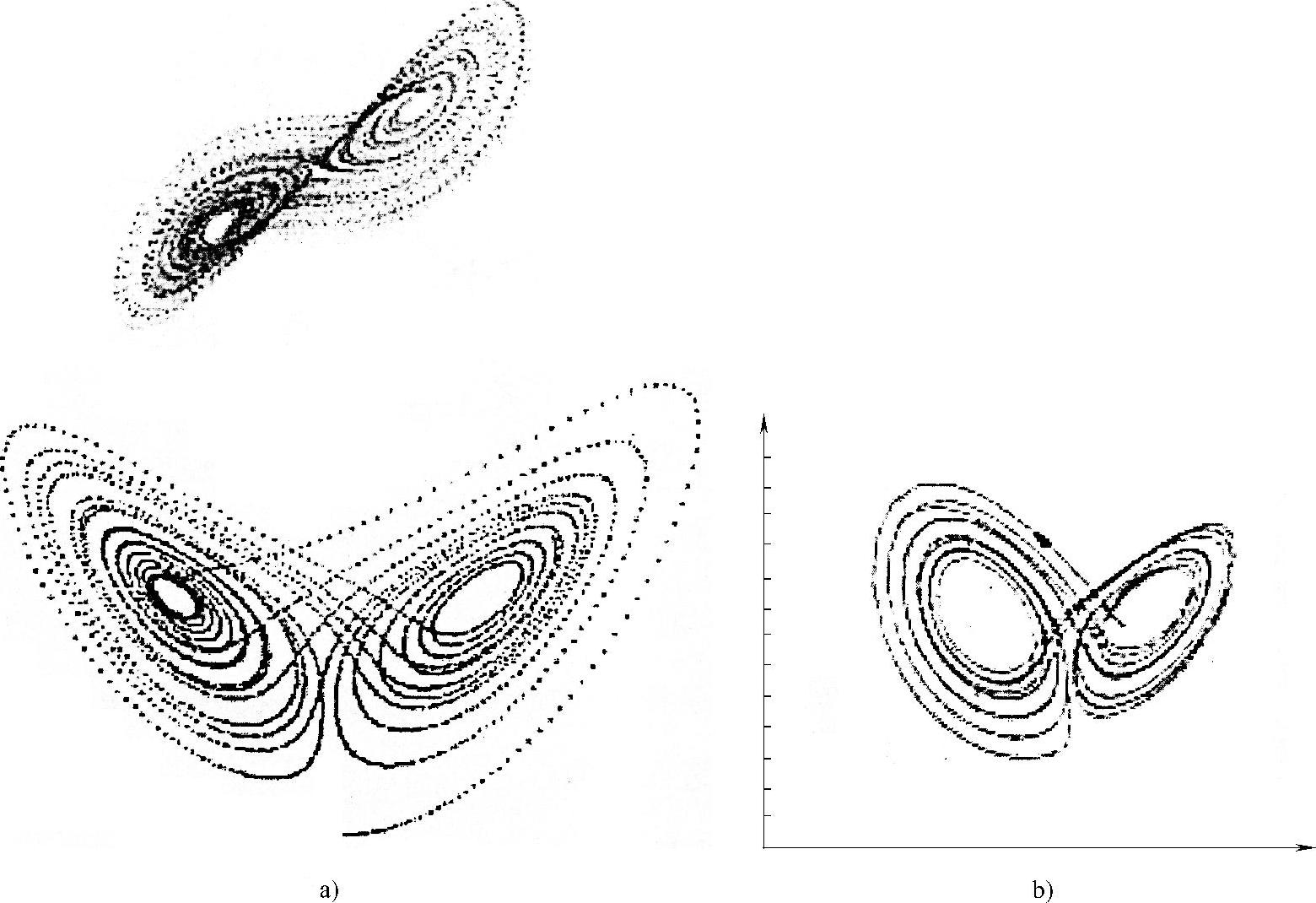
图2-8 混沌吸引子

a）混沌吸引子的形态 b）单模激光系统中的混沌吸引子

6.蝴蝶效应

简单的热对流现象居然能引起令人无法想象的气象变化，产生所谓的“蝴蝶效应”。原来某地下大雪，经追根究底却发现是受到几个月前远在异地的蝴蝶拍打翅膀产生气流所造成的。这说明系统初始状态的微小变化可引起以后巨大的反应，即“差之毫厘，失之千里”。

7.分岔和分岔点

从一个平衡态就转到另外一个平衡态，就是分岔，这个交界的点就是一个分岔点。分岔是一类问题中有多个性质上完全不同的解交叉在一起，这个交叉点就是所谓的分岔点；第二，分岔一般伴随有事物性质上的突变，一种状态变为性质上差别很大的另外一种状态；第三，分岔是实质的非线性问题。

8.倍周期分岔

倍周期分岔是指一个映射的稳定周期随着参数增大而加倍地分岔的现象，经过倍周期分岔就能进入混沌。

9.李雅普诺夫指数

李雅普诺夫指数是表示相邻轨线间的平均发散（分离）率，是一个统计平均量。系统对初值敏感（即对混沌现象）的判断需要一个定量的指标，这个指标就是李雅普诺夫指数，这个指数必须为正。