矢量变换控制系统优化方案

1.矢量变换控制的基本原理

转差频率控制虽然有较好的控制效果，但与直流调速相比，差距仍大。因此必须另行开发新的控制系统，首先研制成功的是矢量变换控制系统（简称矢量控制系统），一直沿用至今。

大家知道，直流电动机调速之所以得到高性能的转矩、转速控制，是由于电枢电流和磁场磁通可以分开独立控制，异步电动机却不能做到。异步机的转矩可写成

M＝K_MΦI₂ cosφ₂ （1-28）

式中 I₂——转子电流；

cosφ₂——转子电路功率因数。

由于这些电磁量为交流电磁量，笼型转子电流I₂又不能测量，故直接对Φ、I₂独立分开控制是困难的。但是矢量变换控制技术通过坐标变换能够将交流量变成直流量，就能对磁通和电流进行独立控制，此种控制技术的基本思路是按照产生同样的旋转磁场的等效原则建立起来的。

变换过程是：首先将紧密耦合的三相交流ABC系转换为两相交流αβ系（3／2），再将其转换为与直流电动机的直流dq系（αβ／dq），这样就可以将交流量解耦，便可以将Φ、I₂分开控制，其过程如图1-39所示。控制结束得到控制给定值是直流量，必须经过反变换到交流量去控制逆变器，驱动电动机按要求运行，即从dq系反变换到αβ系（dq／αβ）再变换到ABC系（2／3）。如果控制系统采用转子磁场定向，dq系改用MT系表示，如图1-39c，M轴与d轴重合，M轴与T轴相差90°，αβ系与MT系变换和反变换称为旋转变换。

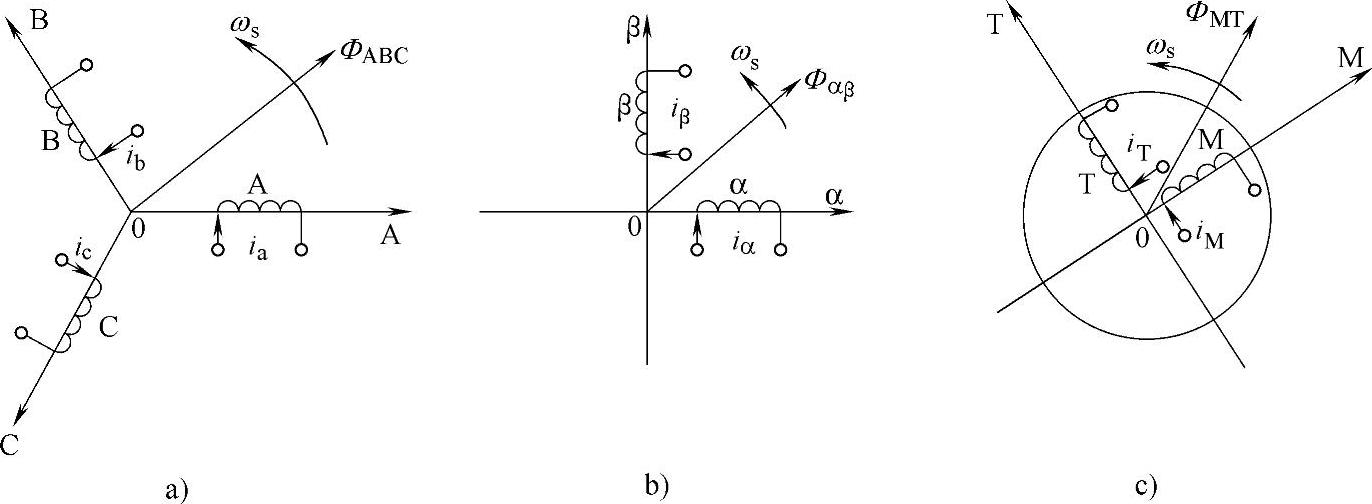
图1-39 异步电动机等效模型

a）三相坐标系 b）两相坐标系 c）M－T坐标系

按照变换原则，ABC坐标系和αβ坐标系的变换与反变换（叫做Clark变换）、αβ坐标系和MT坐标系的变换与反变换（叫做Park变换）以电流量为例，经过变换分别为

i_αβ＝A_1ABC （1-29）

反变换i_ABC＝A₁^－1i_αβ

i_MT＝A₂i_αβ

反变换i_αβ＝A₂^－1i_MT

i_MT＝A₂i_αβ＝A₂A₁i_ABC

反变换i_ABC＝A₂^－1A₁^－1i_MT

经过推导

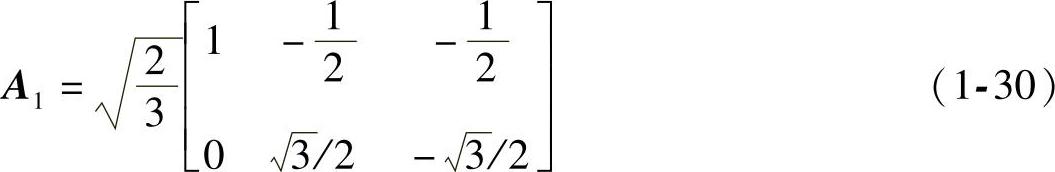
逆矩阵

(www.xing528.com)

逆矩阵

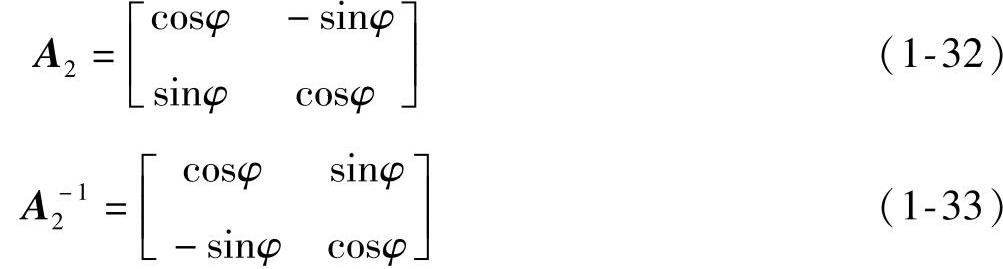
式中φ－M轴与α轴的夹角。

通过两次变换，可得到励磁电流i_M、转矩电流i_T，并可计算转矩［见附录1］。

2.控制系统的构成与控制原理

根据上述思路，可设计出矢量控制系统，已有几种方案，这里采用常用的转子磁场定向的速度、磁链闭环的控制系统，其框图如图1-40所示，所谓转子磁场定向，就是将转子磁链ψ_r与M轴相重合。

系统控制过程如下：

（1）从电动机定子侧测出定子电流i_a、i_c，i_a、i_c经abc坐标系→αβ坐标系变换（3／2变换）得i_α、i_β，定子电压u_ab、u_bc也经3／2变换得u_α、u_β；i_α和i_β送αβ／MT系换算就得i_M、i_T，这就是直流量作为系统的反馈量。u_α、u_β在转子磁链观测器中用下列公式运算，得到｜ψ_r｜和sinφ、cosφ作为运算参量。

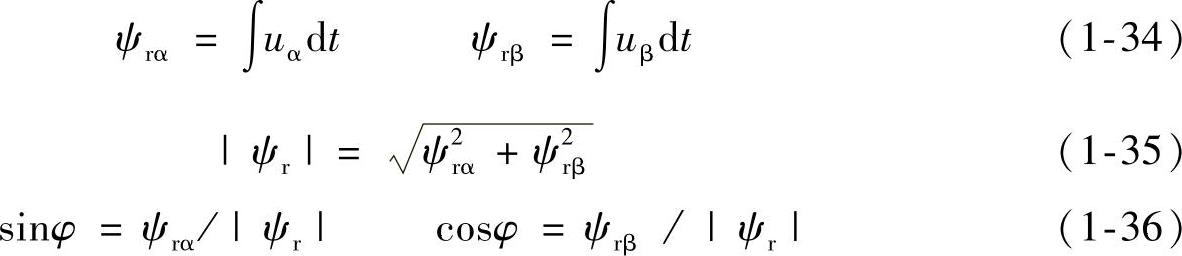
（2）从图1-40可看到，系统有两个输入端，其一是转速给定n∗，与实测转速n比较后进入速度调节器得到转矩给定T_e∗，经除法器除以｜ψ_r｜即得电流给定i_T∗，与实际i_T比较后进入电流调节器PI再经电流电压变换器就得到电压给定为u_T∗。

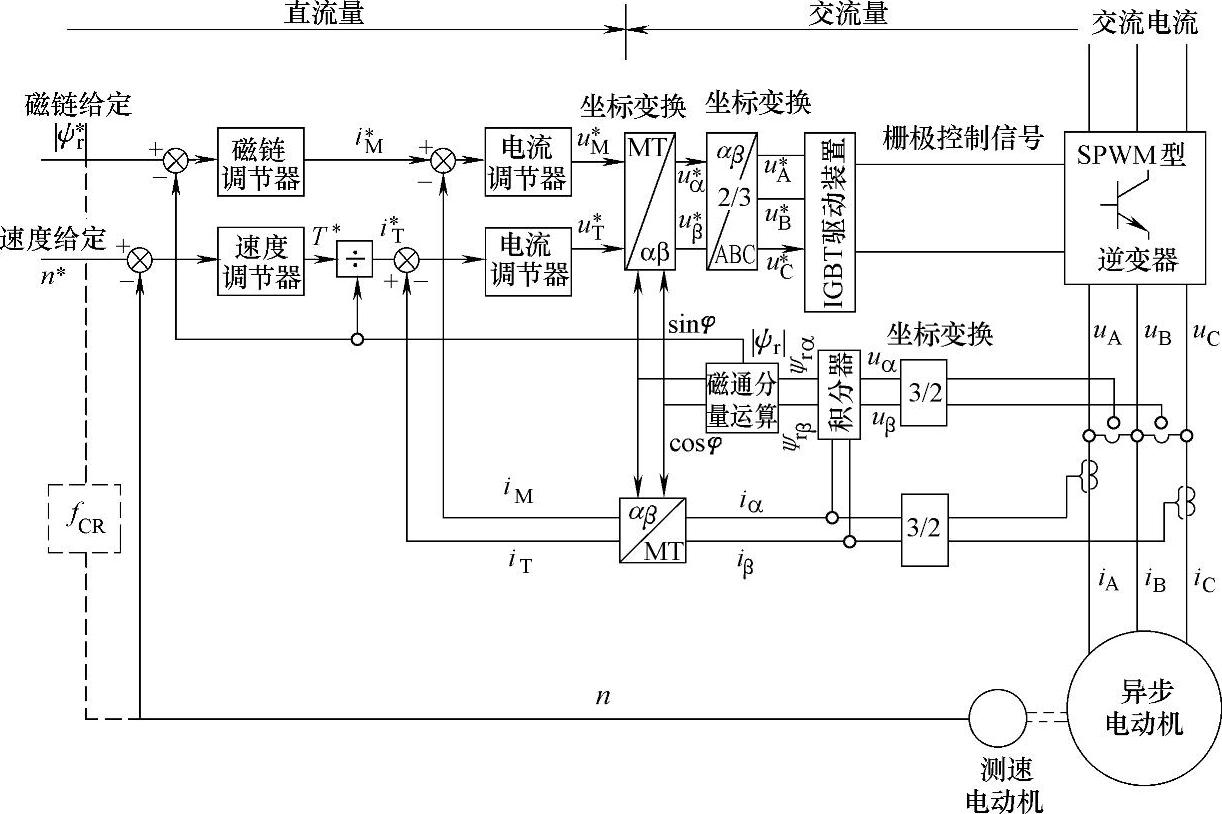
图1-40 转子磁场定向矢量控制系统

电压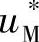，这时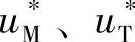都是直流量，故要经过MT／αβ变换得到交流给定量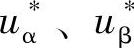，再经2／3变换得到三相电压给定量，送入逆变器驱动装置驱动逆变器工作，控制到此结束。

这个例子属于有速度传感器的系统，还有无速度传感器的系统，其区别是用转速观测间接算出实际转速值。

3.矢量变换控制的特点

20世纪70年代，德国西门子公司F.Blasche等人提出的“感应电动机磁场定向的控制原理”和美国P.C.Cstman与A.A.Clark申请的专利“感应电动机定子电压的坐标变换控制”奠定了矢量控制的基础。以后经过不断改进，形成了当今普遍采用的变频调速系统，现在的厂商生产的变频器产品大部分应用这种系统。矢量控制有下述特点：

1）经过矢量变换，可以具有直流电动机的控制性能，调速精度高，并具有恒功率控制、转矩按比例控制等优良的特性。

2）动态响应快，且可控制失速转矩。

3）起动转矩大。低速时，采用减小转矩脉动的措施可扩大调速范围。

4）采用SVPWM技术还具有输出谐波小、转矩脉动小、直流利用率高、易于数字化等优点。

5）矢量控制的不足之处是控制比较复杂，控制特性受电动机参数的影响较大，需要输入准确的数据，一般不易得到。