如何进行机构的等效代换优化？

机构的等效代换是指两个机构在输入运动相同时，其输出运动也完全相同，这样的两个机构可以互相代换，以满足不同的工作要求。

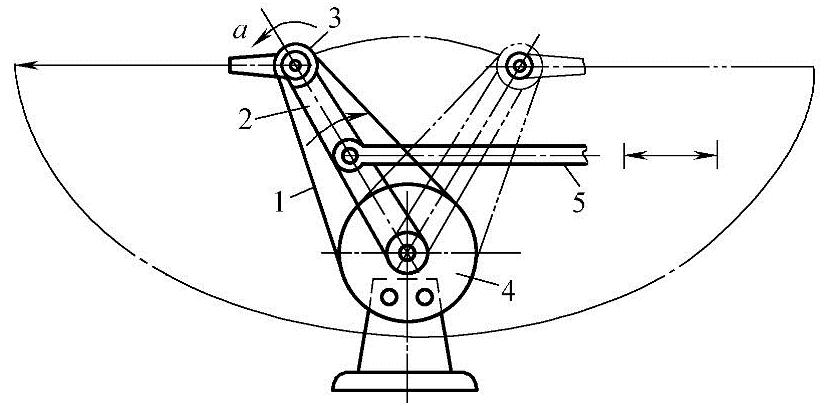
图3-59 清洗机构

1—挠性件 2—转臂 3—行星带轮 4—固定带轮 5—连杆

1.利用运动副的替代原理进行等效代换

前文已经介绍了平面高副与低副互相替代的原理，利用这个原理完全可以进行机构的等效代换。例如对于各种偏心盘的凸轮机构可被相应的连杆机构代换，或反之，如图3-60所示，其中图3-60a是尖底推杆偏心盘形凸轮机构与曲柄滑块机构的等效代换；图3-60b是滚子摆杆偏心凸轮机构与曲柄摇杆机构的等效代换；图3-60c是平底摆杆偏心盘形凸轮机构与摆动导杆机构的等效代换。

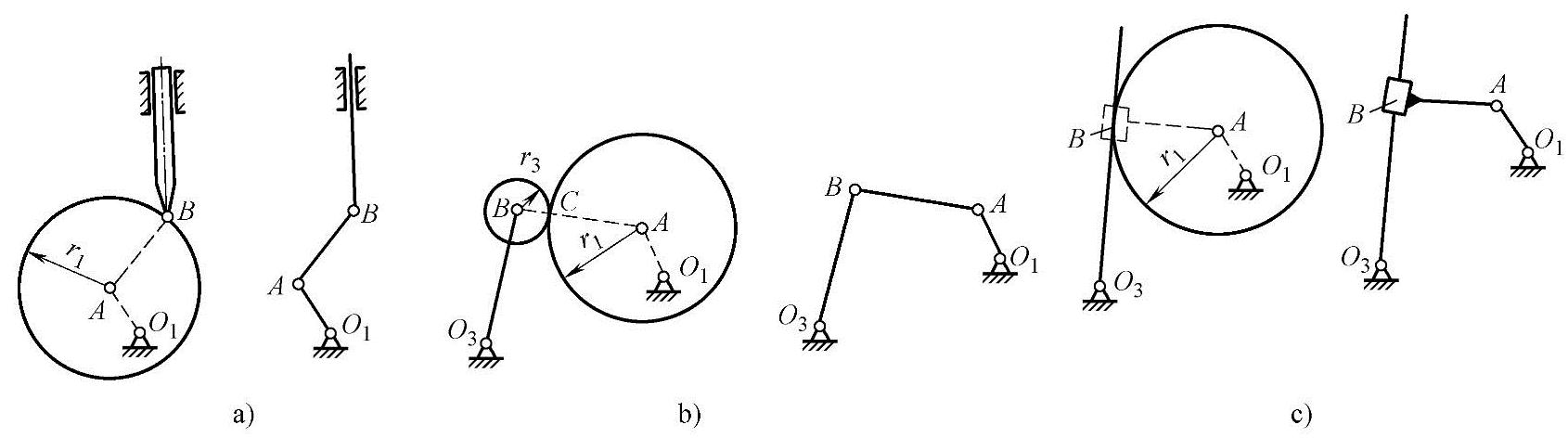
图3-60 偏心凸轮机构与连杆机构的等效代换

从以上等效代换实例可以看出，当高副接触点的瞬时速度中心位于一定点时，就可以实现完全的代换，而不是瞬时的代换。也可以看出若用高副机构等效代换低副机构必须构造代换构件的瞬心线。

2.利用瞬心线构造等效机构

图3-61为一铰链四杆机构ABCD，连杆2与机架4的绝对瞬心为P₂₄。根据三心定理很容易确定P₂₄位于AB和DC的延长线交点上，把机构运动的各个位置的P₂₄点连成曲线，即为连杆2的定瞬心线，如图3-61a所示。

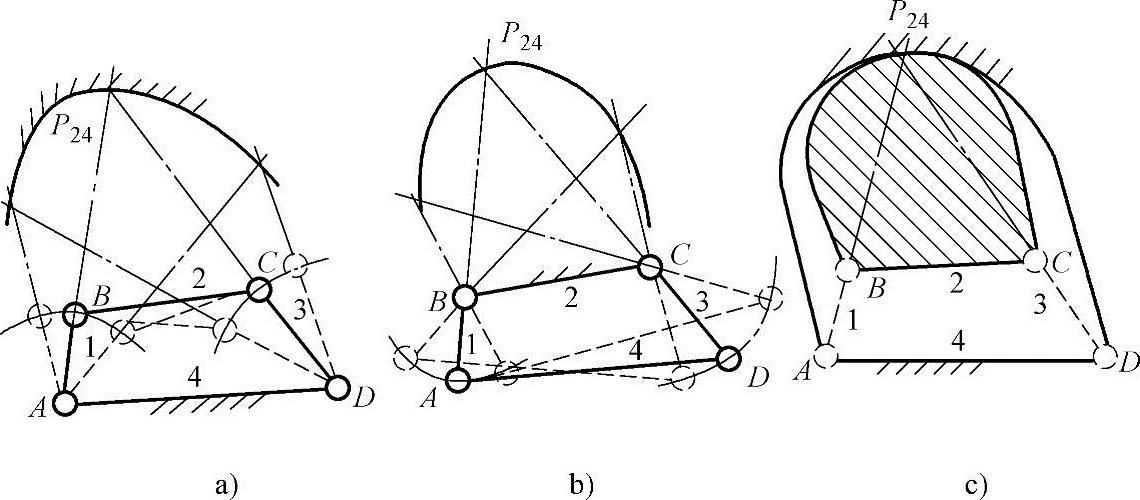
图3-61 铰链四杆机构的等效代换

1—曲柄 2、3—连杆 4—机架

这种等效代换的实用价值在于能克服连杆机构的极限位置所存在的运动不确定问题。例如反平行四边形机构，当从动曲柄与连杆两次处于共线位置时，从动曲柄将出现运动不确定情况，也就影响了这种机构的工作性能。为解决这一问题，可以利用瞬心线构造一个等效机构取代。因为要实现杆1相对于杆3的运动等效代换，则构造瞬心线时应分别以杆1或杆3为机架，然后去掉连杆2。如图3-62所示，构造出反平行四边形的等效机构为椭圆高副机构，该高副机构可以设计成椭圆齿轮机构。

正置曲柄滑块机构是对心式曲柄滑块机构一种特例，即曲柄长OA等于连杆长AB。该机构的特点是，当曲柄回转一周时，滑块的行程是曲柄长的4倍。可以在结构尺寸较小的情况下实现较大的位移，但当曲柄运动到与机架垂直位置时，滑块的运动将不确定。为解决这一问题同样采用上述方法构造一个等效机构进行代换。因为要实现的是连杆2上B点的位置要求，所以在构造瞬心线时应分别以杆2或杆4为机架。他们分别是两个圆，其中定瞬心线圆的半径是动瞬心线圆的半径的2倍，如图3-63所示。若将两个瞬心线的圆当作两个节圆，圆O为固定的内齿轮，圆A为行星轮，保留连杆1作为行星架，并且要求两轮的齿数比为z₄／z₂=2。这样当行星架1转动时，行星轮节圆上任何一点（例如B点）的轨迹均为通过点O的直线，并且当杆1转过一周时，B点的行程是杆1长度的4倍，如图3-64所示。

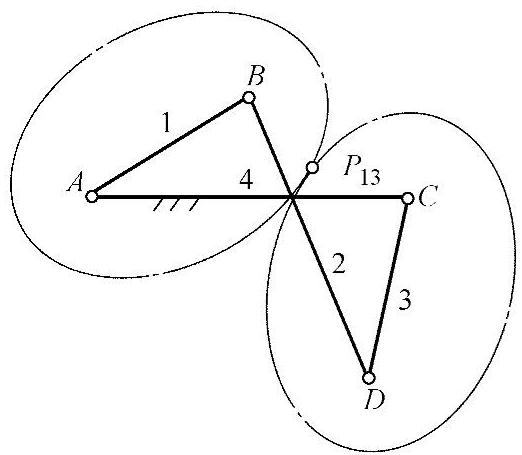
图3-62 反平行四边形机构的等效代换

1—曲柄 2、3—连杆 4—机架

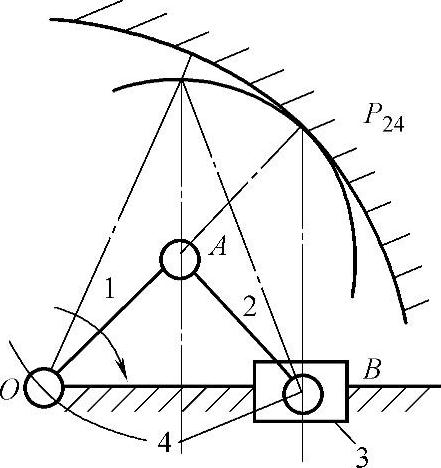
图3-63 正置曲柄滑块机构的等效代换（1）

1—曲柄 2—连杆 3—滑块 4—机架

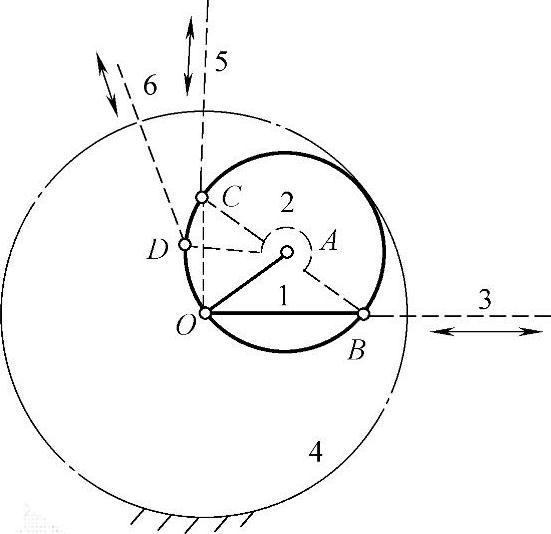
图3-64 正置曲柄滑块机构的等效代换（2）

1、2、4—构件 3、5、6—B、C、D的轨迹线

(www.xing528.com)

图3-65 周转轮系的等效代换（1）

1—行星架 2—行星轮 3—机架

3.周转轮系的等效代换

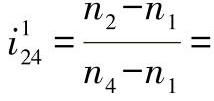
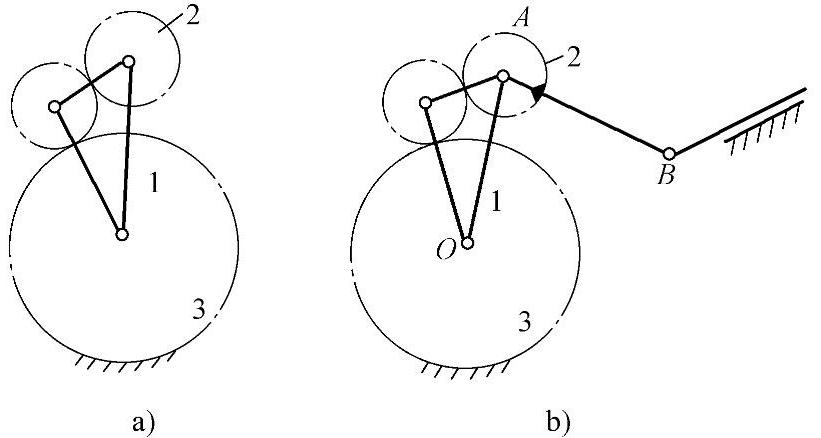
图3-64所示的行星齿轮机构的结构尺寸大，并且内齿轮加工成本高，给使用者带来诸多不便。为解决这一问题可以利用不同结构，但具有相同输入、输出的周转轮系进行等效代换。图3-64所示的周转轮系部分的转换机构的传动比是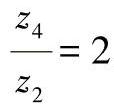。若将原来的内啮合变为外啮合，并保持传动比不变，即z₄／z₂=2，同时增加一个介轮保持原来的方向不改变，就构造了一个与图3-64完全等效的机构，如图3-65a所示。若在行星轮上固连一杆，并使AB=OA，如图3-65b所示，当行星架1转动时，B点输出移动的行程是杆1长的4倍。

将机构进一步简化，用同步带或链传动代换外啮合的齿轮传动，可以去掉介轮，构造一个带有挠性件的周转轮系。若也在行星轮2上固接一个杆，使AB=OA，如图3-66所示，当行星架1转动时，B点输出移动的行程是杆1长的4倍。该机构常用于有大行程要求的场合。

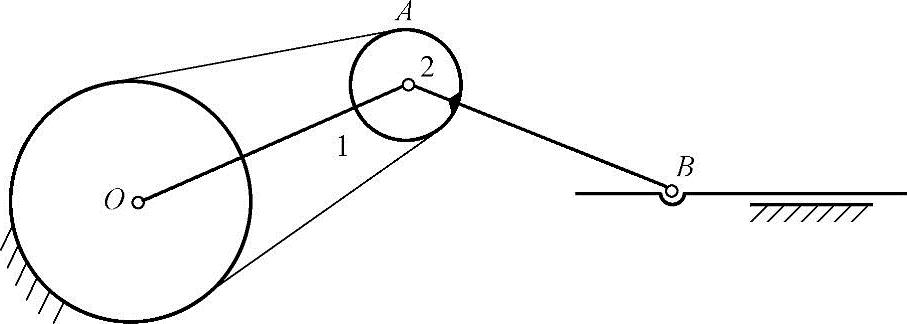
图3-66 周转轮系的等效代换（2）

1—行星架 2—行星轮

4.机构功能的等效代换

利用各种非刚性材料的特性进行机构运动功能的等效代换，这是一种简化机构结构的有效途径。例如图3-67所示的钢带滚轮机构，钢带的一端固定在滚轮上，另一端固定在移动滑块上，当滚轮逆时针转动时，中间钢带将缠绕在滚轮上而拖动滑块向右移动。当滚轮顺时针转动时，两侧钢带将缠绕在滚轮上而拖动滑块向左移动。它等效于齿轮齿条机构，适用于要求消除传动间歇的轻载工作场合。

图3-68是利用纤维材料扭曲与放松而导致其缩短伸长的特性，采用该材料制成可移动连杆，用以实现从动件的摆动。

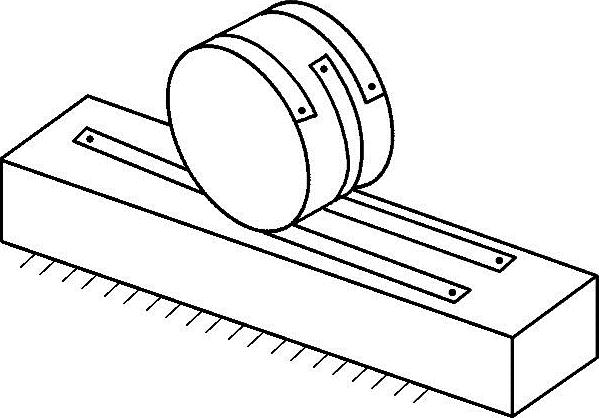
图3-67 钢带滚轮机构

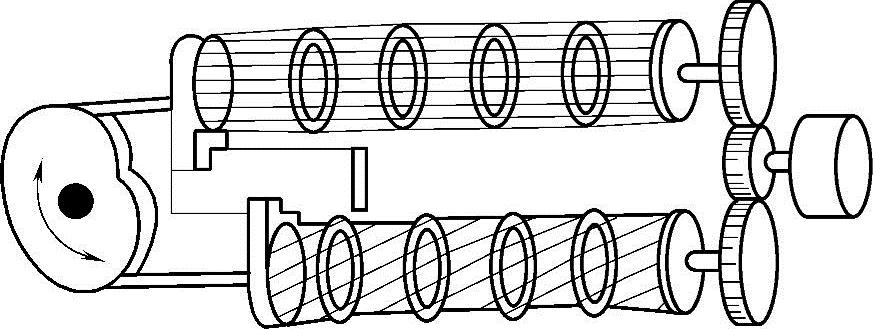
图3-68 纤维连杆机构

图3-69是利用弹性元件变形实现间歇运动。图中构件2的两端与输出转动轴构成转动副，构件2的转臂间装有扭簧4，扭簧的一端固定在构件2上，并与转轴3之间有配合。当构件2逆时针转动时，扭簧被放松，转轴3不受影响而保持静止状态；当构件2顺时针转动时，扭簧被拧紧而紧固在转轴3上使转轴3转动。该机构可以看作是棘轮机构的等效机构，但结构简单，并且没有噪声。

图3-70是两种往复摆动机构的等效代换。其中图3-70a是曲柄摇块与齿轮齿条的组合机构，其工作原理是，曲柄8输入转动，齿条导杆9做平面运动，致使摇块摆动；而导杆9上的齿条又使齿轮11实现往复摆动的输出。该机构可以实现较大的摆动角。但齿条导杆9与滑套10之间存在的摩擦力影响了传动效率；并且齿轮与齿条间的侧隙也影响了齿轮往复摆动的精度。

而图3-70b作为图3-70a的等效机构则克服了上述缺点，它被称为无背隙的往复摆动机构。该机构由框架1、齿形带2、无轴的圆柱形浮轮3（无齿）、齿形带轮4、调整螺钉5、输出轴6、主动曲柄7输入连续转动，使框架1做平面运动，致使齿形带运动，从而带动与其啮合的齿形带轮实现绕固定轴的摆动；螺钉5用来调节带2的张紧程度。该机构的特点是，传动无间隙，并且齿形带的弹性可以吸收换向时的柔性冲击。

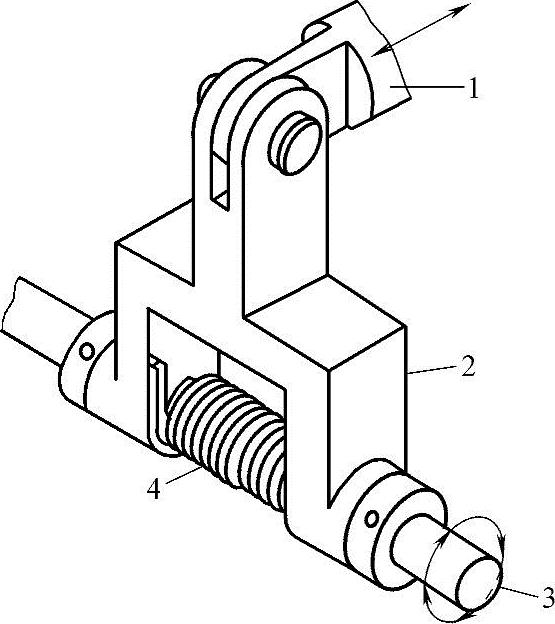
图3-69 弹性间歇机构

1、2—构件 3—转轴 4—扭簧

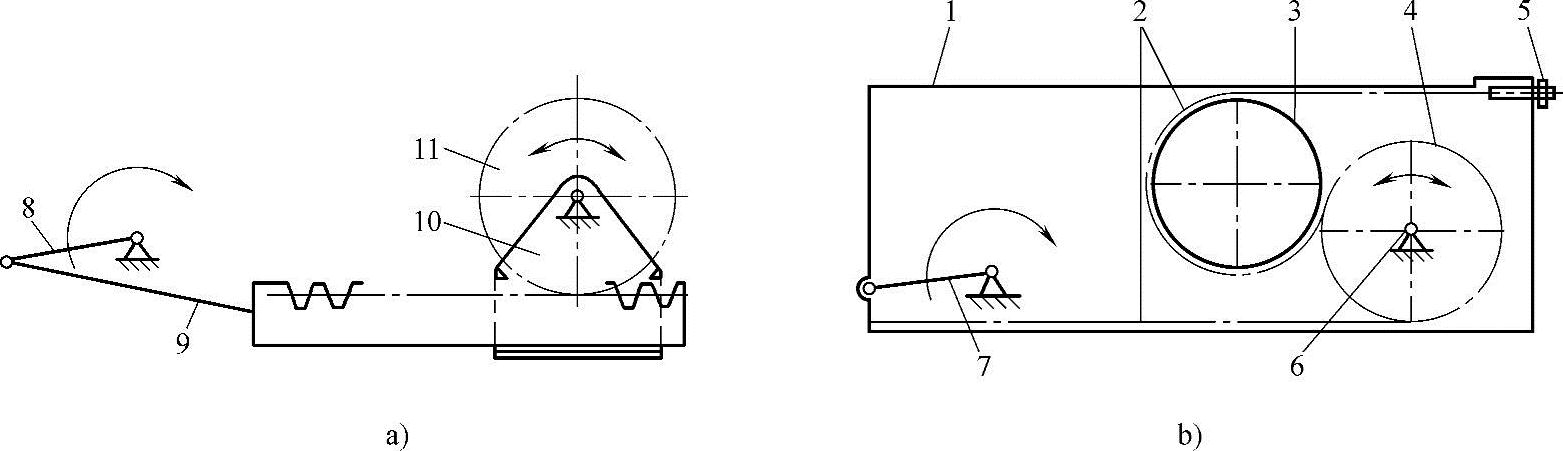
图3-70 摆动机构的等效代换

a）曲柄摇块齿轮齿条机构 b）无背隙往复摆动机构

1—框架 2—齿形带 3—圆柱形浮轮 4—齿形带轮 5—调整螺钉 6—输出轴 7—主动曲柄 8—曲柄 9—导杆 10—滑套 11—齿轮