幅度键控（ASK）信号的产生和解调

1.幅度键控信号的产生

假设数字信号S（t）用脉冲序列表达式为

式中 ak为随机变量。对于二进制来说，当第k元码为1时，ak＝1；当第k元码为0时，ak＝0。S（t）与载波信号uC相乘后，得到幅度键控信号，可表示为

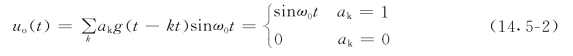
则数字幅度键控信号波形如图14.5-1所示。在式（14.5-1）中，每一元码所占的时间周期为T，它的倒数为码速，单位为比特/秒（bit/s或b/s）。与模拟调制中的调幅相似，幅度键控信号波形的包络线就是数字信息。所以，当使用的载波频率ω0比较低时，数字信号的码速不能高，否则会出现失真现象。式（14.5-2）所表达的是双边带调制信号，图14.5-2给出了ASK调制的模型及原理框图，其他形式的幅度键控也可应用。

图14.5-1　数字幅度键控信号波形

(www.xing528.com)

图14.5-2　ASK调制模型及原理框图

（a）ASK调制模型；（b）ASK调制原理框图

2.幅度键控信号解调

对于模拟调制信号来说，在调制和传输的过程中必然要受到干扰，解调后的信号不可避免地存在失真。因此，模拟信号的解调，除合理选择解调方法之外，特别注重滤波器的设计。然而，对于数字信号来说，允许幅度检波器输出的信号有一定的失真，只需用适当的方法“鉴别”出各码元的真实含义（1或0），恢复原本的数字序列，就等于将干扰造成的失真完全消除。

图14.5-3（a）为包络线检波器构成的ASK信号解调原理框图，图14.5-3（b）为相敏检波器构成的ASK信号解调原理框图；14.5-3（c）为解调波形图。与模拟信号不同的是增加了判决电路，其最简单的形式是一个比较器，当低通滤波器的输出信号uL（t）高于EP时，被判决为“1”，低于EP时，被判决为“0”。判决电路通常使用施密特触发器，并令触发电平等于判决电平EP（EP＝U/2）。可想而知，鉴别出码元真实可信的前提就是低通滤波器输出uL（t）的高、低电平失真不能过大，判决电平EP过高或者过低，判决就可能产生差错。因此，通常使用采样－判决电路，图14.5-4是使用该电路的解调原理框图及波形。由图中可以看出，在2T至3T之间，码元1的后沿还未衰减为零，就进入采样时刻（3T），码元0就有可能误判为1。这就需要在设计低通滤波器时，应根据码速来设定响应的时间常数（截止频率）。

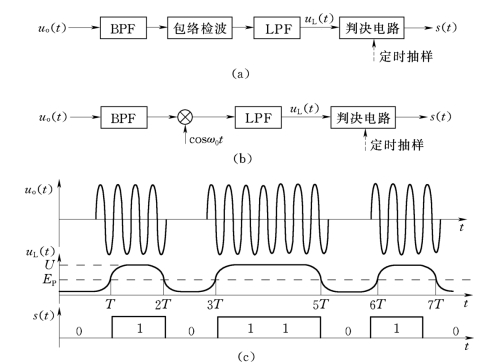
图14.5-3　ASK信号解调原理及波形

（a）包络检波解调原理；（b）相敏检波解调原理；（c）解调的波形图