调幅原理：信号的调制与解调

用测量信号u（t）去控制载波信号的振动，使已调波的包络线按照u（t）的规律线性变化的过程，被称为调幅。假设测量信号为

载波为

则已调信号可以写成为

式中 m——调制系数或调幅度，m＝Um/A0。

用三角公式展开式（14.1-3）可得到

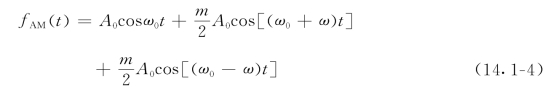
这说明，调幅波由三个频率分量组成，第一项为载波；第二项为上边波；第三项为下边波。

其调幅波波形及频谱图如图14.1-1所示。

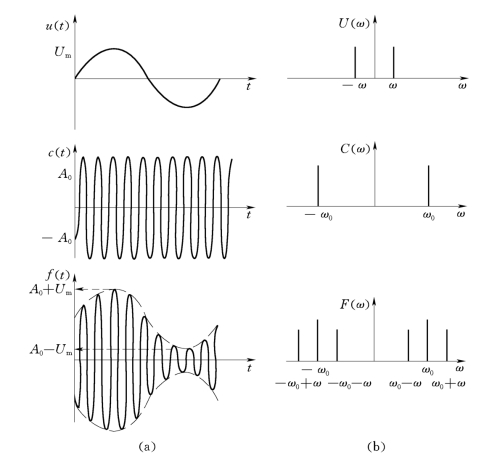
图14.1-1　调幅波波形及频谱图

（a）调幅波波形；（b）调幅波频谱图

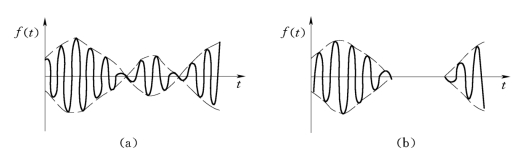
从图14.1-1（a）可看出，A0－Um＞0即m＜1，才能保证调幅波不出现过调制现象，否则在A0－U（t）＝0处使载波相位产生180°的反转，形成包络线失真［如图14.1-2（a）］；如使某些元件出现截止，过调波会如图14.1-2（b）所示。

(www.xing528.com)

图14.1-2　过调幅失真

（a）相位反转失真；（b）截止失真

从图14.1-2（b）中可看出，调幅过程使测量信号的频谱搬移了±ω0，如果测量信号的最高频率为ωm，则调幅波占有2ωm的带宽。所以为了保证频带不重叠，及包络线不失真，应使ω0≫2ωm。

上述调幅被称为标准调幅（AM），主要是利用加法运算和乘法运算，其数学模型可表示为图14.1-3。在实际组成调幅器时，通常只需在乘法器中加上一定的直流偏值即完成加法作用。但由于直流分量A0不是调制信号中的一部分，因此在还原信号时，必须要滤掉，而且它占据了AM波中一半以上的功率。为了提高调制效率，只要在AM波中令A0＝0即可达到目的。式（14.1-3）被写为

图14.1-3　AM波数学模型

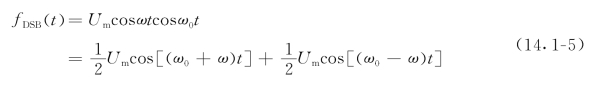
式中 仅包含上边波和下边波，所以被称为双边带调幅（DSB）。DSB波的波形及频谱图见图14.1-4，其数学模型见图14.1-5。

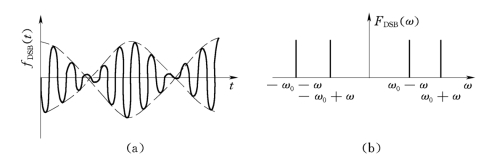
图14.1-4　双边带波波形及频谱图

（a）DSB波波形；（b）DSB波频谱图

实现DSB调制，原则上可以用任何非线性器件或时变参数电路实现乘法功能。通常是采用平衡调制器（如交流电桥），因为它简单稳定，且平衡性能好。但由于u（t）改变符号时载波相位出现倒相点，故其包络形状不再与u（t）的形状相同，而是按|u（t）|的规律变化，因此解调电路要比AM解调电路复杂。

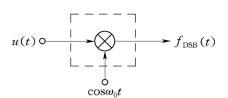
图14.1-5　DSB波数学模型

由式（14.1-5）可看出，上边波或下边波中都包含了u（t）的全部信息，所以只要任意一个边波就足够了。在双边带调制器后面接上一个边带滤波器，抑制掉无用边，即可产生单边带波，这样的调制过程称为单边带调幅（SSB）。