低通滤波器简介

图13.2-1（a）所示是最简单的一阶RC低通滤波器电网络。输入信号为Ui（t），输出信号为Uo（t）。应用电路理论，可求出该网络的传递函数k（s）为

式中 τ＝RC称为该网络的时间常数。用s＝jω带入，可得

式中 幅频特性为

相频特性为

该网络的频率特性如图13.2-1（b）和图13.2-1（c）。

当ω≪时：A（ω）≈1，φ（ω）≈0，该网络可以看成不失真的传输系统。

图13.2-1　一阶RC低通滤波器及频率特性

（a）RC网络；（b）幅频特性；（c）相频特性

当ω＝时：A（ω）＝0.707，φ（ω）＝－45°，依截止频率的定义可知ωc＝，因此，调整RC数值，就可以改变低通滤波器的通频带。如果ω＞ωc则进入过渡带，对频率高于ωc的信号分量开始起衰减作用，其衰减率为－20dB/十倍频程。

当ω≫时：A（ω）＝0，φ（ω）＝－90°，滤波器呈现高阻状态。

实际工作的RC滤波器如图13.2-2所示，由上述分析该网络的截止电压又可写成，fc，可用RC来调整。R与C的组合值主要取决于电容C，通常都在几百pF以上。如果C过小，负载上的输入电容CL及传输导线的分布电容等，都对滤波器的电容有影响。电阻R的值也不能过小，因为信号源内阻Rs与R串联，所以过小的R不但会使信号源的负载加重，而且会使滤波器的截止频率下降，误差增大。但是，R值也不能过大，滤波器的输出是R与C的分压结果，过大的R值会使Uo衰减，同时作为负载的输入电阻，会对负载电路产生不利的影响。通常控制R上的压降在1V以下。

二阶低通滤波器如图13.2-3所示，是用两个低通滤波器串联获得的。图13.2-3（a）中网络的传递函数为

图13.2-2　工作中的RC网络

式中 二阶电网络的时间常数为(www.xing528.com)

二阶电网络的阻尼系数为

令s＝jω代入式（13.2-5）可得二阶网络的频率特性为

考虑到时，二阶网络处于最佳阻尼状态，并且ω＝ωc时，A（ωc）＝0.707。则可求出截止频率

从式（13.2-6）和式（13.2-7）看出，τ与ξ关联紧密，选择合理的ωc，有可能不是最佳。

通常令R1＝R2＝R，C1＝C2＝C，式（13.2-6）和式（13.2-7）可写成

代入式（13.2-8），并让A（ωc）＝0.707，可求出

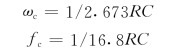
图13.2-3（b）所示网络中使用了隔离放大器，所以该网络的传递函数写成

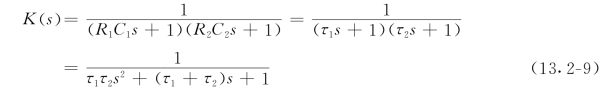
式中τ1＝R1C1，τ2＝R2C2分别为两个串联一阶滤波器的时间常数。

比较式（13.2-5）和式（13.2-8）可知，由于没有隔离器的网络中两个一阶低通滤波器存在负载效应影响，所以电阻和电容之间的关联比较紧密。有隔离器的网络中，两个一阶低通滤波器是相互独立的，可以写成K（s）＝K1（s）K2（s），截止频率取一阶低通滤波器中截止频率最小的一个。

图13.2-3　二阶RC低通滤波器

（a）二阶RC网络；（b）有隔离器的二阶RC网络

二阶低通滤波器的衰减率为－40dB/十倍频程，可以类推n阶低通滤波器的衰减率为－20ndB/十倍频程。从上述分析可看出，二阶滤波器的过渡带比一阶滤波器要窄，但网络结构复杂了，因此调试工作量增大，使用隔离放大器可以使问题简单化。