精密折点电路设计方案探讨

精密折点电路多用于传感器非线性输入特性的线性化。图12.2-5所示电路中来自传感器的输入电压为Ui，E为基准电压。可得运算放大器的输入电压U－为

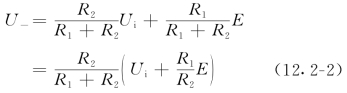
图12.2-5　精密折点电路

U－＞0即Ui＞－时，运算放大器输出为负，VD2导通VD1截止，电路输出Uo＝0。

U－＝0即Ui＝－时，运算放大器输出为零，VD2和VD1都截止，电路输出Uo＝0。

U－＜0即Ui＜－时，运算放大器输出为正，VD1导通VD2截止，电路输出可表示为

(www.xing528.com)

式（12.2-3）相当于端基拟合直线y＝a0＋kx，其中。用端基拟合直线实现折线逼近法及电路如图12.2-6所示，其中。如果需要整个检测系统线性化，通常由图12.2-6（b）所示放大电路实现，参数ai和ki可以用下述方法求得。

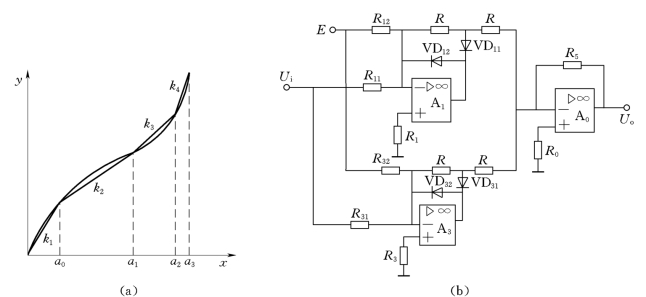
图12.2-6　折线逼近法及电路

（a）折线逼近法；（b）电路

图12.2-7中u1＝f1（x）为放大电路之前的非线性特征（在第Ⅰ象限），y＝f3（uo）为放大电路后面的非线性特性（在第Ⅲ象限），y＝kx是检测系统的线性特性（在第Ⅳ象限），图12.2-7（a）描述了检测系统方框图。将这三条特性曲线分别画在第Ⅰ、Ⅲ、Ⅳ象限。从系统的理想特性y＝kx上任取一点S1出发，分别做平行于x轴的直线与y＝f3（uo）交于R1点，平行于y轴的直线与u1＝f1（x）交于P1点。过P1做平行于x轴的直线，过R1做平行于y轴的直线，二直线的交点为Q1。改变S1的位置，可以得到一系列的Q1点，这些点的连线即为放大电路的特性曲线。而这条特性曲线又可用图12.2-6所示的折线逼近法实现。

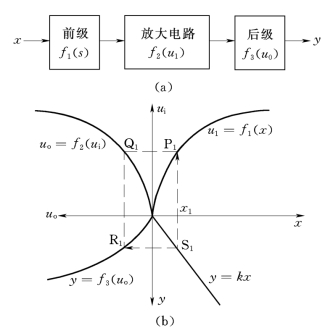
图12.2-7　线形化放大电路的求取

（a）检测系统方框图；（b）uo＝f2（u1）的求取