阻抗电桥的工作原理和应用

在图11.2-1所示交流电桥中，四个桥臂可以是电阻或阻抗元件。其输出电压表达式为

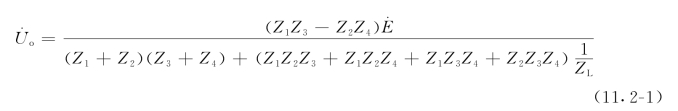
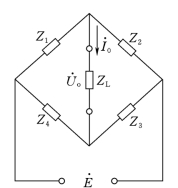
图11.2-1　交流电桥

在测量前，电桥输出电压为零，可得电桥的平衡条件：Z1Z3＝Z2Z4。正弦交流电压供桥情况下，各桥臂阻抗用复数表示为

则平衡条件分为幅值和相角两部分，写作

在测量时，设各桥臂阻抗的变化量分别为ΔZ1、ΔZ2、ΔZ3、ΔZ4，并且ZL＝∞，由式（11.2-1）得到电桥的开路输出电压为

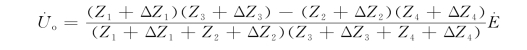
考虑到平衡条件Z1Z3＝Z2Z4，且Zi≫ΔZi展开上式后忽略分母中的（ΔZ1＋ΔZ2）、（ΔZ3＋ΔZ4）及分子中ΔZ1ΔZ2、ΔZ3ΔZ4项，有

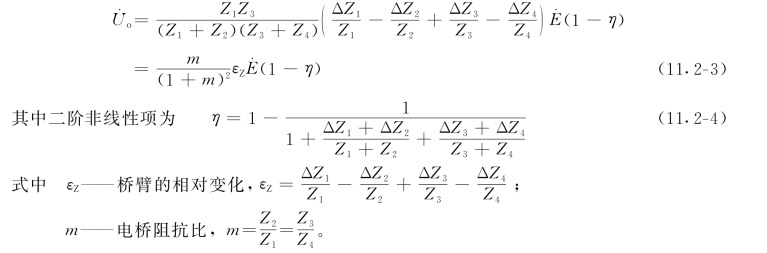
1.单臂电阻平衡电桥

设工作桥臂为Z1，测量时增量为ΔZ1，其他桥臂为固定值，增量ΔZ2＝ΔZ3＝ΔZ4＝0。忽略非线性项后，由式（11.2-3）可得

式中 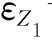说明了传感器感受被测量的能力。相同被测量下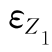，愈大，说明传感器转换能力愈强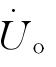，也就愈大。m可影响电桥的灵敏度，m过大会使电桥灵敏度降低。但由于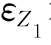和m都是复数，也要考虑相角对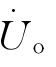的影响。

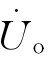（1）与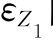的关系表明了工作臂本身对输出的影响。

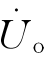由于正比于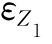，用复数表示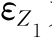为

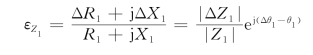
从上式可看出，如果被测量变化产生的增量仅为ΔR1（即Δθ1＝0），则工作桥臂为纯电阻情况，可以达到最大值；如果被测量变化产生的增量仅为jΔX1（即Δθ1＝±π/2），则工作桥臂为电抗情况，可以达到最大值。即传感器的阻抗是纯电阻（电阻式传感器）或纯电抗（电感式传感器和电容式传感器），工作桥臂也应是纯电阻或纯电抗。

除纯电阻和纯电抗两种极限情况之外，要想获得较大的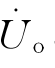，则必须满足Δθ1－θ1＝0，即让工作桥臂的阻抗相角等于接入此桥臂的传感器阻抗相角。

（2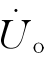）与m的关系表明了工作桥臂与相邻桥臂之间的关联关系对输出的影响。

由式（11.2-5）可知，要使输出电压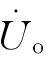为最大，另一个要求是使k＝m/（1＋m）2有极大值。而

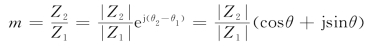
式中 θ——Z2支路与Z1支路的阻抗相角差，θ＝θ2－θ1。

由此可得

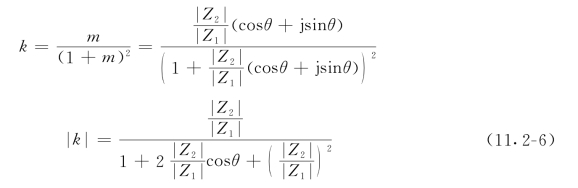(www.xing528.com)

由于θ＝θ2－θ1只可能在－π/2到π/2之间，所以式（11.2-6）中cosθ≥0。要想|k|取得最大值，只有cosθ＝0，即θ＝±π/2。如果工作桥臂Z1是纯电抗，则桥臂Z2应是纯电阻，又因为m＝Z2/Z1（或m＝Z3/Z4），匹配成对称桥就有Z3＝Z2是纯电阻，Z4＝Z1是纯电抗。由电路理论可知，对称电桥输入的端点和输出的端点可以互换，不影响电桥的输入-输出关系。所以，也可得到Z1＝Z2是纯感抗，Z3＝Z4是纯电阻的匹配关系［见图11.2-2（a）］。

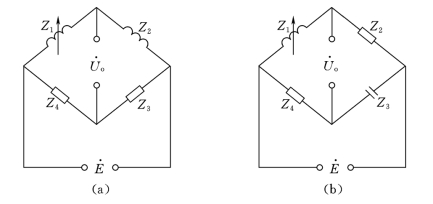
图11.2-2　工作桥臂为纯电感的单臂桥

（a）Z3、Z4为纯电阻；（b）Z2、Z4为纯电阻

当工作桥臂Z1为电抗（θ1＝±π/2），而相邻两臂Z2和Z4为纯电阻时，由电桥平衡条件式（11.2-2）可知θ3＝θ1，所以桥臂Z3必须是与Z1相角相反的纯电抗［见图11.2-2（b）］。

实际应用中，电感线圈有等效电阻，电容器有损耗电阻，连接线有等效电感和耦合电容等，使得电桥的四个桥臂不可能是纯电阻或纯电抗。只要工作桥臂与一个相邻桥臂的阻抗相角愈大，交流电桥的灵敏度就愈大。

灵敏度

非线性由式（11.2-4）可得

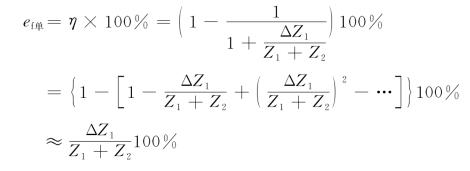
2.差动桥

设Z1和Z2在测量时产生的增量分别为ΔZ1和ΔZ2，差动工作状态下，ΔZ1＝－ΔZ2＝ΔZ，由式（11.2-3），且忽略非线性项得到

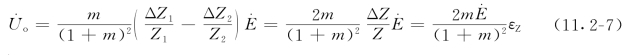
灵敏度为

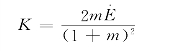
非线性由式（11.2-4）可得

交流电桥中的单臂桥、差动桥和全桥，依然可以按照直流电桥的推导方法得出如下结论：

灵敏度为

非线性为

由于交流桥的平衡条件可分为幅值条件和相角条件，见式（11.2-2），所以在匹配各桥臂时，不只是满足幅值条件，更重要的是注意相角条件。如半桥电路中，两个桥臂用固定电阻，则另两个桥臂（工作桥臂）的阻抗应一致。

3.交流电桥的平衡

图11.2-3所示是几种常用的电阻、电容调平衡的电路形式。交流电桥要满足幅值和相角两个平衡条件，必须反复调节两个桥臂或全部桥臂的参数，才能使电桥完全达到平衡。如图11.2-3（a）是通过调整RW来改变R1和R2上的并联容抗值，使它与L1和L2相平衡。平衡范围与C0有关，C0愈大，平衡范围愈大。

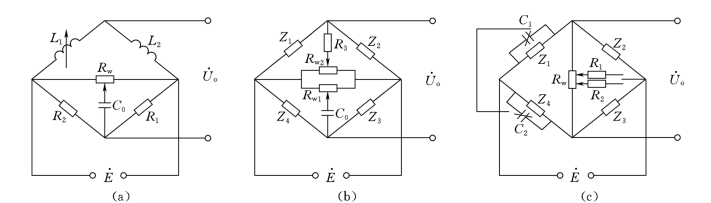
图11.2-3　电阻、电容调平衡电路