常用电桥电路分析方法

1.单臂桥测量电路（惠斯登电桥）

电桥中任一桥臂（假设R1）为传感器的转换元件（如电阻应变片），其它桥臂为固定电阻。当测量时，转换元件电阻值发生变化，其增量为ΔR1（见图11.1-2），各固定电阻增量ΔR2＝ΔR3＝ΔR4＝0，由式（11.1-9），式（11.1-10）和式（11.1-11）都可得到

式中 ε——电阻应变片的应变值，ε＝。

单臂桥的灵敏度为

线性度根据式（11.1-7）可得

2.半桥测量电路（差动桥）

将传感器的两个转换元件分别接入相邻的两个桥臂中，（假设R1和R2），另外两个桥臂为固定电阻，构成卧式桥或立式桥。图11.1-3所示卧式桥可得

对于卧式桥通常R1＝R2＝R，R3＝R4＝R′，在传感器的两转换元件在各项性能参数都应一样时，就有

从上式看出，要想得到足够大的输出电压，其参数增量应保证为ΔR1＝－ΔR2＝ΔR，即在相同的非电量作用下，一个转换元件的增量为正，另一个转换元件产生的增量为负。在图11.1-3中的两个电阻应变片，一个受拉产生正增量，一个受压产生负增量，称为差动。

图11.1-2　单臂电桥（惠斯登电桥）

图11.1-3　卧式电桥

图11.1-4　全桥

卧式差动桥输出电压为

卧式差动桥灵敏度为

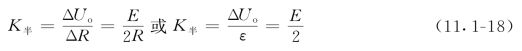
线性度由式（11.1-7）可得，即

立式差动桥的输出电压、灵敏度和线性度请读者自行推导。

3.全桥测量电路

电桥的四个桥臂都接入了转换元件，当测量时四个桥臂的电阻均随被测量变化。图11.1-4所示，全桥可按式（11.1-6）写出开路输出电压为

如果四个桥臂的转换元件性能参数完全一致（即匹配成等臂桥），R1＝R2＝R3＝R4＝R，上式可简化为

(www.xing528.com)

为了让电桥有高灵敏度，设两两相邻桥臂是差动关系，且ΔR1＝－ΔR2＝ΔR3＝－ΔR4＝ΔR，可得到等臂差动全桥的输出电压，即

全桥灵敏度为

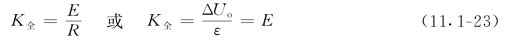
线性度为

对于卧式差动全桥和立式差动全桥的输出电压，灵敏度和线性度，请读者自行推导。

通过对电桥电路的分析，可以知道：

（1）上述分析所得到的结论均是负载电阻为无穷大（即RL＝∞）情况下推导出来的。如果电桥输出端接内阻等于零的检流计（即RL＝0），则据式（11.1-1）可知电桥输出电流为

考虑测量前“电桥平衡”，有R1R3＝R2R4，且测量时各桥臂的电阻增量ΔR1、ΔR2、ΔR3和ΔR4，代入式（11.1-25），并略去高阶无穷小项，可得测量时的电流输出，即

如果称输出是电流形式的电桥为电流桥，那么输出是电压形式的电桥为电压桥。从式（11.1-6）和式（11.1-26）可知，电桥的开路输出电压和短路输出电流有相似的灵敏度和线性度式。当有一定的负载电阻时，从式（11.1-2）和式（11.1-1）可知，电压桥中RL愈小，灵敏度降低，非线性增大；电流桥中RL的影响则相反。

（2）全桥的灵敏度比半桥高，半桥的灵敏度比单臂桥高，它们的关系是

（3）差动半桥和全桥的线性最好，且灵敏度高（不考虑RL的影响）。半桥和全桥构成差动的原则是两相邻桥臂产生相反的等量变化。如果不能构成差动桥，要想增加灵敏度，通常采用图11.1-5所示串联式和并联式单臂桥线路。此方法在半桥和全桥中同样适用。

（4）差动桥能够自动补偿某些外界干扰对输出的影响。这是利用电桥相邻又相等的两桥臂同时产生大小相等、符号相反的电阻增量，不会破坏电桥平衡的特性来达到补偿目的的。

图11.1-5　并联式和串联式单臂桥

例如，图11.1-3所示，卧式半桥中R1和R2在受温度影响时产生的电阻增量分别为ΔR1t和ΔR2t，由被测量引起的电阻增量分别为ΔR1和ΔR2，则总增量分别为

代入式（11.1-16），可写成

由于性能参数一致的R1和R2受相同温度影响，即ΔR1t＝ΔR2t；并且它们是差动工作，ΔR1＝－ΔR2＝ΔR则有

图11.1-6　感光电路

结果与式（11.1-17）一样，既提高了灵敏度，又得到了温度的补偿。

如果不能构成差动电桥，也可让相邻桥臂接入性能参数完全一致的转换元件，它不参加测量工作，但它既作为固定桥臂又作为补偿元件，与参加测量的转换元件一起，感受外界的干扰。图11.1-6所示感光电路，光敏三极管VT1和VT2型号相同，VT1是测光元件，VT2不受被测光的照射，但VT1和VT2同时受环境（如环境光变化、温度等）的影响。根据差动电桥的补偿原理，由于VT2的补偿作用，输出电压只与被测光相关。

（5）在两个相对的桥臂中接入转换元件的测量电路，因为不能产生互相补偿的作用，并且非线性明显增大，所以不被采用。

（6）要得到精确的测量结果，供桥直流电源E必须稳定。设电源的波动值为ΔE，应保证ΔE≪E。