涡流传感器阻抗特性分析

在涡流检测中，传感器的阻抗特性可以分成三种：空载阻抗特性、一次阻抗特性、二次阻抗特性。

1.空载阻抗特性

当传感器处于自由空间，不与导体相耦合的情况，即为空载特性状态，这是传感器调试时的一种原始状态。空载时，传感器的等效电路如图3.3-2所示。L1为线圈的自感，R1为线圈的损耗电阻，C为并联电容，Rs为电容损耗电阻、振荡电阻和传感器的输入电阻。为了简化讨论，仅用虚线内的R1、L1来描述传感器的阻抗特性Z0，用下式表示为

此时，传感器的品质因数Q＝ωL1/R1。

图3.3-2　空载时等效电路

图3.3-3　有耦合时等效电路

2.一次阻抗特性

当传感器与已知物理性质的被测物体耦合时的阻抗，即被测体的材料一定时，它与传感器间的位置变化时的阻抗特性被称为一次阻抗特性。依图3.3-1可得到等效电路如图3.3-3所示。图中R1、L1为传感器的损耗电阻和自感，R2、L2为被测导体的等效损耗电阻和自感，为传感器激励电压，M为传感器线圈与被测体间的互感量。依图列出回路方程如下

传感器线圈受到被测导体影响后的等效阻抗为

式（3.3-4）中实数部分是等效损耗电阻，是互感M的函数，互感量随着传感器与被测体之间的距离x的缩小而增大，这一变化与被测导体是不是磁性材料无关。式中虚数部分是传感器的等效电抗，它分为两项。第一项ωL1中的L1与静磁效应有关，即与被测导体的导磁性能有关；而第二项与涡流效应有关，一般称为涡流效应的反射电抗。当传感器与被测导体的距离x减小时，静磁效应使传感器的等效电感L增大，而涡流效应却使传感器的等效电感L减小，这两种效应是相反的。因此，当被测材料是软磁材料时，以第一项变化为主，因而在传感器接近被测导体时，传感器的等效电感量L增大；如果被测导体为非铁磁材料或硬磁材料时，第一项变化不显著，而以第二项变化为主，因此传感器的等效电感L则减小。根据上述分析涡流传感器可以把传感器与被测导体之间的距离x值变换成传感器的等效阻抗值或等效电感值。

涡流传感器的品质因数Q值用下式表示

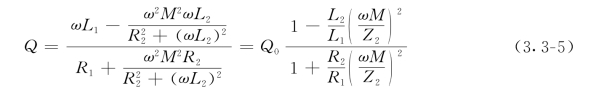
式中 Q0——无被测导体影响下的Q值，Q＝ωL1/R1；(www.xing528.com)

　　 Z2——被测导体中电涡流部分的等效阻抗，Z2＝。

由上式可看出，Q值是互感系数M平方的函数，可表示为

而互感系数M与被测导体和传感器的距离x有关，无论被测导体是导磁材料还是非导磁材料，互感系数M都随x的增大而减小。因此，Q值随x的增大而增大，仅是灵敏度有所差别。另外，Q值与x的特性曲线是非线性的，应尽量利用它的近似线性段。

3.二次阻抗特性

当传感器与未知物理性质的被测物体耦合时，即不同性质的被测材料与传感器间的阻抗特性被称为二次阻抗特性。

在涡流检测技术中，不仅希望解决集合量与传感器输出量的关系，还希望能检测出金属的物理和化学性质有关的参数（例如电导率、硬度）以及缺陷。电感器的阻抗由式（3.3-4）表示，可以看出，由于被测导体的耦合，传感器阻抗与空载阻抗相比发生了变化，其实数部分的增量ΔR为

虚数部分的增量ωΔL为

将式（3.3-7）除以式（3.3-8）可得

式（3.3-9）的物理意义是：对于不同的金属，相应有不同的比值。如果不考虑M（M选择适当），并设ωL2常数，由涡流而引起的电阻增量和电感增量，就由金属电导率所决定。测量金属电阻率时，频率不应选择太高，这一点是很重要的。

如果用式（3.3-7）和式（3.3-8）消去R2，可得

式（3.3-10）的物理意义是：由于传感器与被测导体之间的耦合松紧程度不同，引起传感器阻抗电阻部分与电感部分的变量所遵循的条件不同。当M一定时，式（3.3-10）表达的是一个以（0，ωΔL）为圆心，M2ω/2L2为半径的圆。也就是说，传感器与被测导体的耦合（M）不同，传感器的阻抗变量要遵循不同半径的圆。如果同时考虑R2和M，就必须同时满足式（3.3-9）和式（3.3-10）的条件，那么就是一条直线与圆弧线的交点。

综上所述，根据涡流传感器的基本原理与阻抗特性，可以把被测量变换成三种不同的输出量，即Z、L和Q。虽然他们彼此关联，但配用相应的测量电路，可以分别反映Z、L和Q的变化。