简单实现自感传感器的原理

自感传感器的原理如图3.1-1所示，它是由线圈、铁芯和衔铁三部分组成。铁芯与衔铁之间有一个气隙，气隙厚度为δ，衔铁与铁芯的重叠面积为S。被测物理量运动部分与衔铁相连，当运动部分产生位移时，气隙δ或重叠面积S被改变，从而使电感值发生变化。在图3.1-1（a）中，线圈的电感值可按下式计算

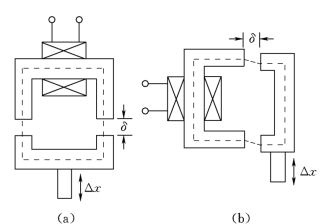
图3.1-1　自感传感器原理

（a）变间隙型；（b）变面积型

式中 w——线圈匝数；

　　 ΣRm——以平均长度表示的磁路的总磁阻。如果气隙厚度δ较小，而且不考虑磁路的铁损，则总磁阻为

式中 li——各段导磁体的磁路平均长度（cm）；

　　 μi——各段导磁体的磁导率（H/cm）；

　　 Si——各段导磁体的横截面积（cm2）；

　　 δ——空气隙的厚度（cm）；

　　 μ0——空气隙的导磁系数（μ0＝4π×10－9H/cm）；

　　 S——空气隙的截面积。(www.xing528.com)

因为一般导磁体的磁阻要比气隙的磁阻小得多，所以计算时可忽略铁芯和衔铁的磁阻，则式（3.1-2）写为由式（3.1-3）可以看出，如果线圈匝数w是一定的，电感L受气隙厚度δ、气隙截面积S和气隙导磁系数μ0的控制。固定这三个参数中的任意两个参数，而另一个参数跟随被测物理量变化，就可以得到三种结构类型的自感传感器。

1.改变气隙厚度δ的自感传感器

该类型如图3.1-1（a）所示，这种传感器灵敏度高，对测量电路的放大倍数要求低。其缺点是输出特性严重非线性，在图3.1-2中给出了L-δ关系曲线。当δ＝0时，L并不等于∞，而是接近于无气隙情况下由导磁体的磁阻决定的自感值，如图中虚线所示。当气隙δ过大时，漏磁增加，灵敏度减小；当δ＝∞时，自感L与衔铁无关，完全取决于铁芯间的空气磁阻（漏磁磁阻）。因此，衔铁的测量行程是非常小的，最大示值范围Δδmax＜0.2δ0，原始气隙δ一般在0.1～0.5mm之间。当被测物理量改变衔铁的位移非常微小时，可用这种类型的传感器进行测量。

2.改变气隙截面积S的自感传感器

图3.1-1（b）给出了这类传感器的原理。它的优点是示值范围较大，具有较好的线性，图3.1-2中所示L-S关系曲线。当S趋向最大值时，由于气隙δ的影响，气隙的磁阻将占主导地位，从而使L趋于常数，出现非线性。该类传感器常用于检测位移或角位移。

3.改变导磁系数μ的自感传感器

图3.1-3所示改变μ的自感传感器的原理。图3.1-3（a）是利用铁磁材料的压磁效应，在受外力作用时，铁磁材料内部产生应力或应力的变化，引起铁磁材料导磁率的变化。该类型传感器用于测量压力、拉力、变矩、扭力、扭矩、重量等。

图3.1-3（b）为螺管式自感传感器。假设线圈内磁场强度是均匀的，电感相对变化量与衔铁插入长度的相对变化量成正比。换句话说，线圈内的导磁性与衔铁插入的长度相关。实际螺管式传感器线圈内的磁场是不均匀的，且衔铁插入的深度不同，泄露路径中的磁阻也不同，因此有一定的非线性。该类型的传感器，自由行程大，示值范围大；制造简单，稳定可靠。它的缺点是灵敏度低。

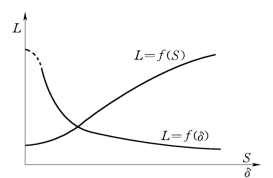
图3.1-2　L-δ、L-S关系曲线

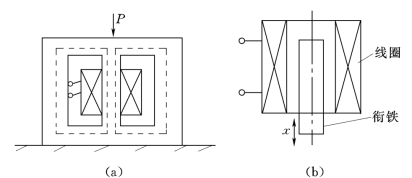
图3.1-3　改变μ的自感传感器原理