传感器的性能指标及一般特性

传感器的输出-输入关系特性是传感器最基本的特性。分析这些特性，是为了掌握一种揭示传感器性能指标的方法，从而全面地去衡量传感器的性能差异及优劣。

传感器的特性一般分为静态特性和动态特性两部分。

1.传感器的静态特性与性能指标

静态特性是指被测量和输出量均处于稳定状态时的输出-输入关系，衡量静态特性的重要性能指标是精确度、灵敏度、线性度、重复度、迟滞（滞环）、分辨率与分辨力等。

（1）误差与精确度。严格讲，无论何种方法，使用何种检测装置，测量得到的结果都与真实的被测量之间存在着一定的偏差。测量值与真值之偏差称为绝对误差Δx，表示为

式中 x——实际值，测量得到的结果；

　　 A0——真值，被测量本身所具有的真正值。由于存在测量误差，根本不可能测量得到真值A0，所以，通常只能用误差非常小的高档标准测量装置所测得值A看做真值，或将无限次测量结果的算术平均值A近似地看做真值。式（1.2-1）改写成

则称为示值误差。

误差描述了测量出来的实际值与真值之间的偏差程度，如测量10mm长度时误差是0.1mm；而测量100mm时，误差也是0.1mm。误差值相同，测量质量谁优谁劣？如果用误差Δx与被测量的平均值A之比来表示

γA称为实际相对误差。结果测量10mm长度的实际相对误差为1%；测量100mm长度的实际相对误差为0.1%。所以相对误差比绝对误差更能确切地说明测量的质量。

误差Δx与测量装置读出的实际值x之比，称为示值相对误差。记为

误差Δx与测量装置的满量程xm之比，称为满度（或引用）相对误差。记为

满度相对误差γm通常用来说明该测量装置的测量质量。

在测量过程中由于传感器设计与制造引起的本身性能的不完善，因为使用方法和安装、调试的不规范，以及使用环境的恶劣等已知因素造成的误差，称为系统误差。产生原因不明确，但服从大多数统计规律的误差，称为随机误差。如图1.2-1示例。

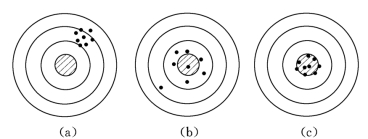
图1.2-1　精密度、准确度与精确度

被射的靶心表示被测量的真值，而射击的弹孔看做传感器的测量输出实际值。由图1.2-1（a）可以看出，每次测量的实际值（弹孔）之间偏差是微小的，这种多次测量的一致性用精密度来表示。在图1.2-1（a）所示测量中精密度很高，但总体偏离真值（靶心）较大。多次测量的平均值与真值的偏差，多是由系统误差引起的，可以通过补偿等方法予以抵消。传感器生产厂家一般给出其修正公式或参数表。图1.2-1（b）所示，多次测量中，大部分距真值非常接近，但有些远远偏离了真值，这种测量值与真值的接近程度用准确度表示，在图1.2-1（b）中说明其测量有一定的准确度，但精密度不够好。其较大的偏离值，多是由随机误差引起的，很难预知它的出现，但可以经多次测量后用滤除法加以消除。如果能够像图1.2-1（c）那样，多次测量的精密度高，准确度也高，将这种既精密又准确的性能称为精确度（简称精度）。在工程上，往往引用精确度等级（简称精度等级）来说明测量结果的可靠程度。该性能指标也适用于动态特性中。

（2）灵敏度和线性度。通常用传感器在静态特性情况下输出的增量与输入（被测量）的增量之比来描述传感器对被测量的敏感程度，称为灵敏度，用k表示

如果传感器的灵敏度k为常数，说明输出-输入关系是一条直线，即

式中 y——输出量；

　　 x——输入量（被测量）；

　　 a0——零位输出；

　　 k——灵敏度。k为常数，可大大简化传感器的理论分析和计算，同时为标定传感器和数据处理带来了方便，这样有利于安装调试，确保测量精度。这就是为什么要将传感器的输出-输入关系作成线性的原因。

实际上许多传感器的输出-输入关系都是非线性的，在不考虑迟滞和蠕变效应的情况下，可用下式表示

式中 a2、a3、…、an——非线性项的待定系数。

由于传感器的输出-输入特性是非线性的，所以经常用一条直线来近似地表示实际的曲线。这种方法称为非线性特性的线性化，被采用的直线称为拟合直线。传感器的实际输出-输入特性曲线，是在静态标准条件下标定的。静态标准条件是：没有加速度、振动、冲击（除非这些参数本身是被测量）、环境温度一般为室温20±5℃；相对湿度不大于85%；大气压力为101327±7800Pa（760±60mm Hg）的情况。在这种标准工作状态下，利用一定等级的校准设备，对传感器进行反复循环测试，得到的输出-输入数据一般用表列出或画成曲线。实际曲线与拟合直线之间的偏差为传感器的非线性误差，非线性误差的最大值与传感器满量程（FS）输出之比（%）称为线性度（或称非线性）。即

式中 Δm——最大非线性误差；

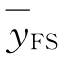　　 ——传感器的满量程输出值平均值。

由图1.2-2可看出，线性度是以拟合直线为基准计算出来的，不同的拟合方法所得到的线性度不同。

下面介绍几种不同线性度的定义和表示方法：

1）理论线性度（绝对线性度）。通常取零点（0%）为起始点，满量程输出（100%）为终止点，连接这两点的直线（y＝kx）即为理论直线。理论线性度表示了标定出的实际曲线与理论直线之间的偏差程度［见图1.2-2（a）］。此方法使用简便，但线性度大，较为粗糙。

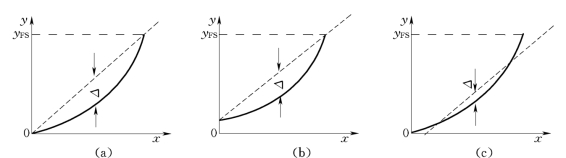
图1.2-2　不同拟合方法下的线性度

（a）理论线性度；（b）端基线性度；（c）平均选点线性度

2）端基线性度。取传感器标定出的零点输出平均值为起始点，满量程输出平均值为终止点，连接这两点的直线（y＝a0＋kx）为端基拟合直线。以此直线为基准可计算出实际曲线与拟合曲线的偏差程度，称为端基线性度［见图1.2-2（b）］。

3）平均选点线性度。1）与2）两方法的拟合精度不高。为此，将标定出的全部数据分成近似相等的两组，并求出两组的点系中心坐标，连接两点得到拟合直线，称为平均选点法。该直线为

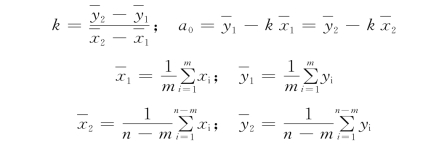
式中 n——所有数据个数；

　　 m——所在点系的数据个数。

以此直线为基准计算的线性度为平均选点线性度［见图1.2-2（c）］。该方法提高了拟合精度，计算也比较简便。

4）独立线性度。选择拟合直线的另一种简单有效的方法是独立直线（端基平移直线）。作两条与端基直线平行的直线，使之恰好包围所有的标定点，然后在这一对平行线之间作一条等距直线，使实际输出特性相对于所选拟合直线的最大正偏差值和最小负偏差值相等。图1.2-3中，独立线性度为±1.1%FS。以独立直线为基准计算线性度时，应将式（1.2-8）改写为

基准直线还有最小二乘法拟合直线，平均斜率拟合直线等，可参阅相关文献。当标定出的实际曲线比较弯曲时，由上述拟合直线为基准计算出的线性度大，测量精度就会降低。通常可采取将实际曲线分割成段，然后用上述某一种方法分段选取拟合直线（见图1.2-4），用分段后的最大线性度代表整体线性度。这种方法被称为折线逼近法，通常用精密折点电路实现，也可在具有CPU的测量装置中非常方便的用软件实现。

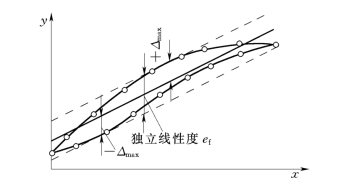
图1.2-3　独立线性度的拟合直线

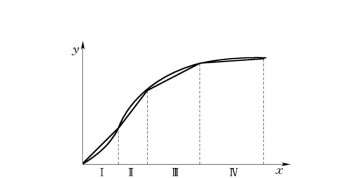
图1.2-4　以端基线为拟合直线的分段线性化方法(www.xing528.com)

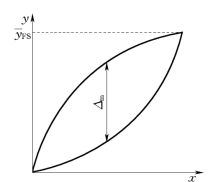
图1.2-5　迟滞特性

图1.2-4所示以端基线为拟合直线的分段线性化方法。不同段的直线表达式y＝a0＋kx中的a0和灵敏度k是不一样的，可列表编制在计算程序中。

（3）迟滞（滞环）。传感器在正向（被测量增大）和反向（被测量减小）时，输出特性曲线不重合的程度，称为迟滞，或称滞环。如图1.2-5所示，对应同一大小的被测量，由于被测量变化到这一值时的正反方向不相同，使得传感器的输出信号值不同。产生迟滞现象的主要原因有传感器机械部分存在不可避免的缺陷，如轴承摩擦、间隙、紧固件松动、材料的内摩擦、积尘等，以及磁滞和电元件的单向特性等等。

迟滞的值通常用多次实验得到正向和反向输出量之间的最大偏差Δm与满量程输出平均值的百分比来表示，记为

（4）重复性。传感器在被测量按同一方向作多次全量程实验时，所得到的输出特性曲线的不一致程度，用重复性来表示（见图1.2-6）。重复性的计算是用多次实验中输出最大不重复误差Δm与满量程输出平均值的百分比来表示，记为

复性误差属于随机性的，由于特定的次数不同，其最大偏差值Δm也不同，所以用标准偏差σ来计算重复性指标比较合理。即

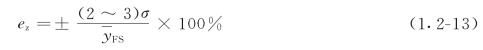
式中 σ——标准偏差，σ＝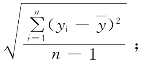

　　 n——实验次数；

　　 yi——第i次实验值；

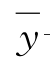　　 ——实验值的算术平均值。

　　 σ前的系数取2时，误差完全依从正态分布，置信概率95%；取3时，置信概率为99.73%。重复性的好坏与许多因素有关，其产生的原因与迟滞相近。

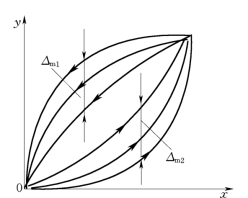
图1.2-6　重复性

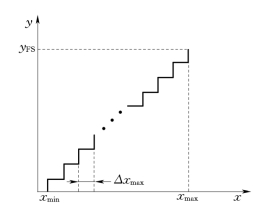
图1.2-7　线绕电位计式传感器的输出

（5）分辨率与分辨力。线绕电位计式传感器，当输入量连续变化时，输出量却是阶梯变化的（见图1.2-7）。无论输出量是阶梯变化还是离散的数字量或频率量，传感器能够测量到的最小输入变化值Δx，称为分辨力。它代表了传感器的最小量程，与输入量同量纲。用分辨率表示传感器的分辨质量，通常有平均分辨率和最大分辨率两种表示方法。

平均分辨率为

式中n——传感器在满量程内，输出的阶梯个数。

最大分辨率为

式中 （Δx）max——输出的最大阶梯所对应的输入量增量；

　　 xmax——输出满量程时对应的输入最大值；

　　 xmin——输出量从零开始变化时对应的输入量最小值。

分辨率是一个无量纲的百分数，有的输出连续变化的传感器也给出分辨率。

随着微处理器的发展和应用，F/V和A/D等电路被更多的集成到传感器的测量电路中，输出量是离散的数字量（或频率量）的传感器愈来愈多，因此，分辨率和分辨力是这些传感器不可缺少的主要性能指标之一。

2.传感器的动态特性与性能指标

在被测量随时间变化的情况下，传感器的输出量跟随输入量变化的能力，用动态特性性能指标来描述。有些传感器的静态性能指标非常好，但响应时间长，测量变化较快的被测量时，会产生非常严重的动态误差，往往动态误差会比静态误差高几倍，甚至几百倍。

图1.2-8　传感器的复域输出-输入关系

用控制理论中的传递函数Φ（S）来表达传感器的输出-输入关系（见图1.2-8），即

Φ（S）的分母X（S）＝在控制理论中被称为系统的特征方程，与输入量X（S）和输出量Y（S）无关，它决定了传递函数Φ（S）的固有特征，也就是传感器的动态特性和静态特性。传递函数可以用建立传感器的动态数学模型或频域的实验方法来确定。

（1）传感器的时域性能指标。通常用典型的阶跃变化作用于传感器的输入，可得图1.2-9中所示的一条传感器输出的阶跃响应特性曲线。图中曲线1是一阶系统或近似于二阶系统的欠阻尼阶跃响应曲线，y0对应的直线为输出y的稳态值。

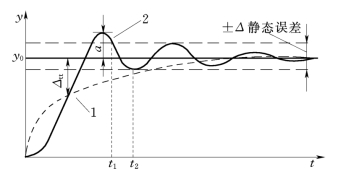
图1.2-9　阶跃响应与时域性能指标

1）响应时间ts：或称建立时间、调节时间，是指响应曲线开始进入静态误差带，并且不再超越静态误差带的时间（见图1.2-9中的t1或t2）。在ts时间段内，响应曲线与稳态值的偏差称为动态误差Δtt。动态误差是随时间变化的量；在ts时间之后，响应曲线进入静态误差带，动态误差小于静态误差指标，此时的动态特性近似于静态特性。

2）可用静态的拟合直线确定输出-输入关系。响应时间ts反映了传感器响应过程的长短，体现了将被测量转换成电量的快速性。

3）过冲量（超调量）σ%：响应曲线第一次超过稳态值时的峰值是传感器输出量与稳态值偏差最大的值a（见图1.2-9）。过冲量σ%用下式计算

过冲量表达了传感器在响应过程中超出稳态值的最大正偏差与稳态值的百分比。过冲愈小，响应过程中的正偏差愈小，响应的平稳性愈好。

（2）传感器的频域特性与性能指标。传感器的输入量为一频率变化的正弦x（t）＝Arsinωt作用时，输出响应也为同频率的正弦y（t）＝Acsin（ωt＋φ）曲线。但由于传感器有一定的响应时间，所以表现为输出曲线迟后于输入曲线相角φ（见图1.2-8）；同时传感器的输出曲线的幅值Ac与输入幅值Ar的比值，也与响应时间有关。用s＝jω代入式（1.2-16）可得到频率响应函数φ（jω），即

式中 P（ω）——复数φ（jω）的实部；

　　 Q（ω）——复数φ（jω）的虚部。

用A（ω）和φ（jω）表示传感器的幅值和相位随频率ω变化的关系，可得

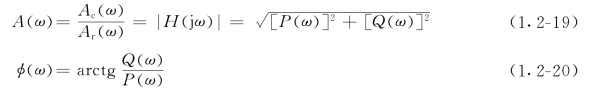
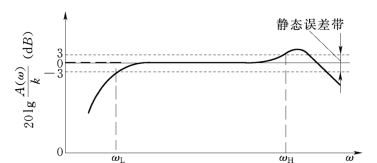
图1.2-10　传感器的对数幅频特性曲线

对于具有低通特性的传感器，当ω＝0时（输入量不变化），传感器的输出-输入关系遵循静态特性关系，此时输出量与输入量之比为k（灵敏度），即A（ω＝0）＝k，则20lg＝0dB，将图1.2-10中的0dB水平线视为理想的幅频特性曲线。有些具有带通特性的传感器，随着输入作用的频率ω的增大，幅频特性A（ω）也要变化，见图1.2-10中，在（ωL－ωH）段，特性曲线近似平直，说明A（ω）是不随ω变化的稳态值。在这段对应的频率范围内传感器的输出不会超越允许的误差带。而在（0－ωL）及（ωH－∞）范围内，A（ω）随着ω的增大而变化，说明传感器的输出-输入幅值比是变化的，灵敏度随ω变化，输出量中有很大的动态误差，且大大超过了允许的误差带。将ωL称为下截止频率，ωH称为上截止频率，（ωL－ωH）频率区间则称为传感器的通频带（或频响范围）。通常表示为

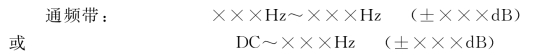
只有被测量的变化频率（包括有用谐波频率）在传感器的通频带之内，传感器才能真实的将被测量测量出来。