【摘要】：BCH码的译码方法可分为时域译码和频域译码两类。时域译码中，1960年彼得森提出了二进制BCH码的译码理论基础。图8-10BCH码译码器方框图下面，以BCH码的译码为例作具体说明。图8-11BCH码的两个除法电路以上电路输出余数综合有三类情况，第一类是无误码，第二类是15位码组中有1位误码，第三类是15位码组中有2位误码，这三类情况均可译码出正确数据信息。表8-4由余数r1、r2确定的误码位置续表
BCH码的译码方法可分为时域译码和频域译码两类。
时域译码中，1960年彼得森提出了二进制BCH码的译码理论基础。彼得森译码仍然利用校验子的计算，通过校验子找寻误码样式，由此得知译码位置并予以纠正，具体可分为四步：
第一步：用g（x）的各因式作为除式对接收的码组多项式求余式，得到t个称为部分校验子的余式；
第二步：对t个部分校验子通过误码位置计算电路构造出特定的误码多项式，它以误码位置作为多项式的根；
第三步：求解误码多项式，得到误码位置的解；
第四步：纠正存在的误码时，原理上是对误码求其反码，具体可用码元“1”与i求模2和。
该方法的译码器方框图如图8-10所示。
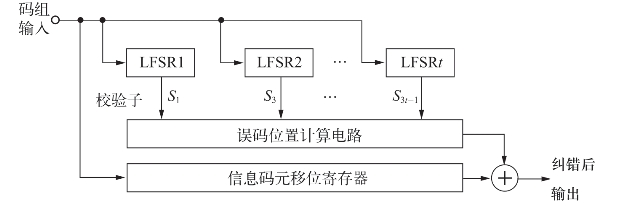
图8-10 BCH码译码器方框图(www.xing528.com)
下面，以BCH（15，7）码的译码为例作具体说明。由表8-3可知，（15，7）码能纠2错，2个生成多项式为
两者的电路构成如图8-11所示，它们对接收码组作除法运算，分别给出余数r1（x）、r2（x），余数范围各为0000-1111。
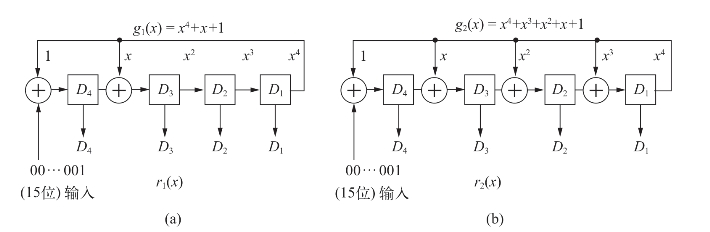
图8-11 BCH（15，7）码的两个除法电路
以上电路输出余数综合有三类情况，第一类是无误码，第二类是15位码组中有1位误码，第三类是15位码组中有2位误码，这三类情况均可译码出正确数据信息。
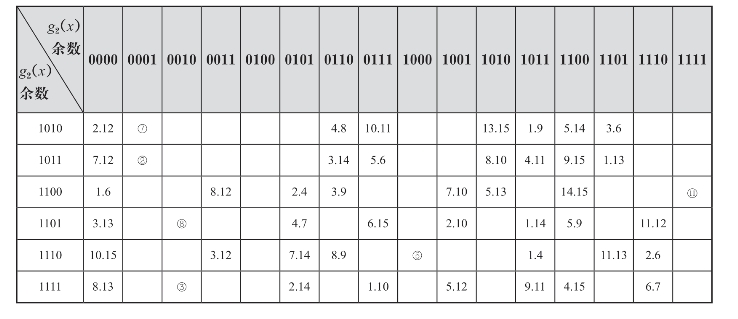
概括上面三类情况，由余数确定的误码位置如表8-4所示。
表8-4 由余数r1（x）、r2（x）确定的误码位置
续表
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
