（一）二元码的误码产生
一种不归零二元码传输过程中受噪声影响产生误码的情况如图8-1所示。
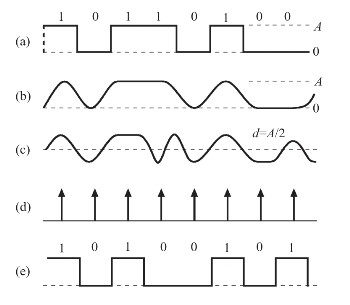
图8-1 二元码产生误码的情况
在图8-1中，图（a）表示原始数据序列的不归零二元码波形；图（b）表示经传输通道中频率特性失真后接收端得到的序列波形；图（c）表示叠加入噪声干扰之后的波形，中间一条虚线表示判决门限电平d（高电平与低电平的平均值），高于d的电平判决为数据“1”，低于d的电平判决为数据“0”；图（d）表示判决定时脉冲；图（e）表示判决后恢复的数据序列。比较图（a）和图（e）可以看出，在两处由于噪声幅度超过判决电平而发生接收误码。
（二）误码率与信噪比的关系
1.误码率
数字信号传输系统中，误码的多少通常以误码率（误比特率BER或误符号率SER）衡量，它表示为单位时间内误码数目占总数据数目的比例值。
2.误码率与信噪比的关系
设二元码数字信号为s（t），信道产生的噪声（平均值为零的高斯白噪声）为n（t），则数字信号经过信道传输后，在接收端的输出信号y（t）为这两者的相加，即：
y（t）=s（t）+n（t）
有高斯白噪声的数字信号波形及噪声能量分布如图8-2所示。
图8-2（a）所示为接收端含有高斯白噪声的数字信号波形，图8-2（b）所示为与信号电平相应的噪声能量分布。由图可见，因噪声影响使信号电平发生失真而超过判决电平的概率是很小的，但在电平判决时刻一旦出现这种情况，就会形成误码。图（b）上示明的曲线交叠部分表示会产生误码的电平范围。(www.xing528.com)
平均值为0的高斯白噪声的幅度概率密度函数P（n）为：
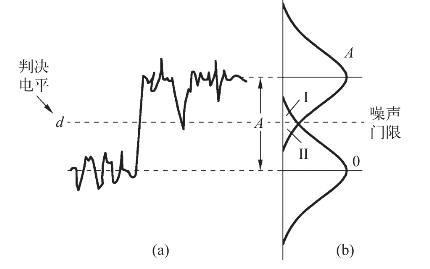
图8-2 有高斯白噪声的数字信号波形及噪声能量分布
式中，σ2为噪声功率，也即噪声均方值。
当发送端传输数据“0”（幅值0）时，叠加噪声后接收端的信号幅度概率密度函数为P0（y）（上式中左边的n=y，右边的n=y）。当发送端传输数据“1”（幅值A）时，叠加噪声后接收端的信号幅度概率密度函数为P1（y）（上式中左边的n=y，右边的n=y-A）。
由此得到P0（y）、P1（y）的函数图形，如图8-3所示。
它们与图8-2（b）相似。图中，判决门限电平选为d=A/2。
由图8-2和图8-3可见，发送信号幅度为0时，如果时钟脉冲判决时刻Y（KT）≥d（图8-2和图8-3中I区内），则接收端判决结果将误认为发送信号的幅度为A；同理，发送信号幅度为A时，如果时钟脉冲判决时刻Y（KT）＜d（图中Ⅱ区内），则判决结果将误认为发送信号幅度为0。这两种情况都造成数据误码。
根据Q函数得到的总误码率Pb与信噪比S/N之间的关系曲线如图8-4所示。
图8-3 高斯白噪声的幅度概率密度函数
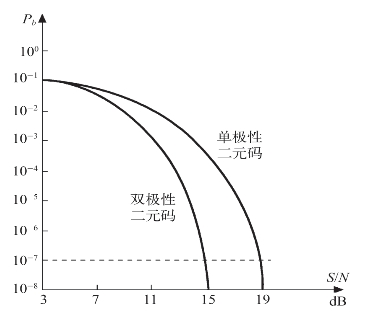
图8-4 总误码率Pb与信噪比S/N之间的关系
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
