信息论原理之统计编码方法

统计编码利用信息论原理减少数据冗余。

（一）信息量和信息熵

对于某一离散无记忆信源X的符号集xi（i=1，2，…，N），假设每个符号xi是统计独立的，出现的概率为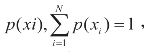则符号xi所携带的信息量定义为：

I（xi）=log2[1/p（xi）]bit

由此可见，出现概率低的符号传送的信息量比出现概率高的符号大。

如果将信源所有可能时间的信息量进行平均，就得到了信源中每个符号的平均信息量，又称为信息的熵，可表为：

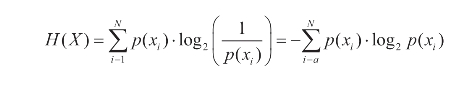
熵是对一个信源进行编码时最小平均码长的理论值，提供了一种可以用来测试无失真编码性能的标准。

利用信息熵的编码方法很多，如哈夫曼编码（利用概率分布特性）、游程编码（利用相关性）、算术编码（利用概率分布）等。

（二）哈夫曼（Huffman）编码

哈夫曼编码利用变字长编码（VLC）：根据符号发送概率的不同分配不同码长的码字。出现概率大的符号给以短码，对于概率小的符号给以长码。

Huffman编码步骤：

第一，把信源符号xi（i=1，2，…，N）按出现概率的值由大到小顺序排列；

第二，对两个概率最小的符号分别分配以“0”和“1”，然后把这两个概率相加作为一个新的辅助符号的概率；

第三，将这个新的辅助符号与其他符号一起重新按概率大小顺序排列；

第四，跳回到第二步，直到出现概率相加为“1”为止；

第五，用线将符号连接起来，从而得到一个码树，树的N个端点对应N个信源符号；

第六，从最后一个概率为“1”的节点开始，沿着到达信源的每个符号，将一路遇到的二进制码“0”或“1”顺序排列起来，就是端点所对应的信源符号的码字。

Huffman编码过程如图7-21所示。

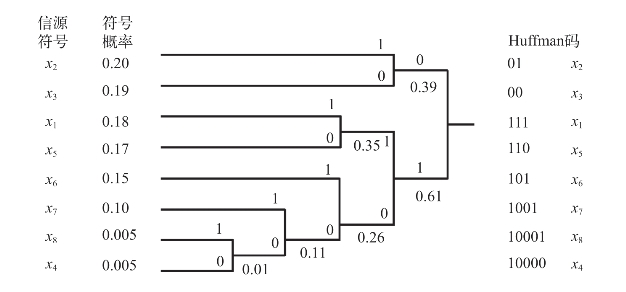
图7-21　Huffman编码1

Huffman编码有如下性质：

首先，码不是唯一的。因为“0”和“1”选择的任意性。但对于同一信源而言，平均码长是相同的，编码效率也一样。

其次，Huffman编码对不同的信源其编码效率是不同的，信源中符号出现的概率相差越大，编码效果越好。

第三，Huffman编码中，没有一个码字是另一个码字的前缀，因此，每个码字唯一可译。

（三）算术编码

在算术编码中，把被编码的信息表示成0～1之间的一个间隔数，在传输任何信息之前，信息的完整范围是［0，1），当一个符号被处理时，区间范围就依据分配给这一符号的那部分范围而变窄。(www.xing528.com)

信息越长，编码表示它的区间就越小，表示这一区间所需的二进制位就越多。

算术编码原理：

设信源字符集X中有N个符号xi（i=1，2，…，N），每个符号的概率为：p（xi）=pi，有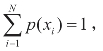编码过程如下：

首先对字符集X中每个单独的符号赋一个0～1之间的子区间，子区间的长度等于该符号的概率，并假设这样的赋值对解码器来说是已知的。

2.读入第一符号a1，设a1是符号集X中的第i个符号，a1=xi（i=1，2，…，N），那么初始子区间定义为：

［l1，r1）=［pi-1，pi）

3.读入下一个符号，设已经是第n次读入，并设读入的符号an是符号集X中的第i个符号，即an=xi。

定义新区间为：

［ln，rn）=［ln-1+pi-1dn-1，ln-1+pi dn-1）

ln表示新区间的左边界值，rn表示新区间的右边界值，ln-1表示上一个子区间的左边界值，rn-1表示上一个子区间的右边界值，dn-1=rn-1-ln-1表示上一个子区间的间隔，pi-1表示当前被编码符号的原始区间的左边界值，pi表示当前被编码符号的原始区间的左边界值。

例如：设信源符号为[x1，x2，x3，x4]，这些符号的概率为p（xi），根据这些概率可将间隔[0，1）分成四个子区间，如表7-1所示。

表7-1　符号概率列表

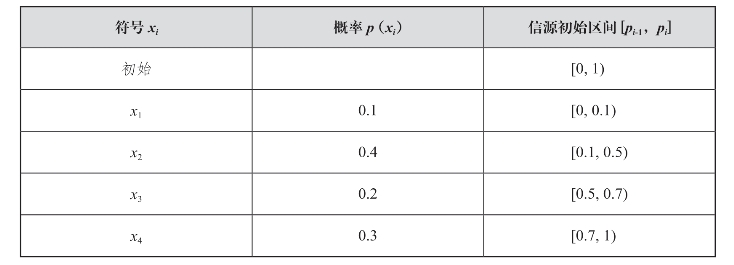
输入信息序列：x3x1x4x1x3x4x

如果输入的信息为x3x1x4x1x3x4x2，区间变化过程如下。

读入第1个符号x3，原始区间是[0.5，0.7），l1=0.5，r1=0.7，d1=0.2，在处理完第1个符号后，区间范围为[0，1）缩到[0.5，0.7）。

读入第2个符号x1，原始区间是[0，0.1），l2=0.5，r2=0.52，d2=0.02，在处理完第2个符号后，区间范围为[0.5，0.7）缩到[0.5，0.52）。

读入第3个符号x4，原始区间是[0.7，1），l3=0.514，r3=0.52，d3=0.006，在处理完第3个符号后，区间范围为[0.5，0.52）缩到[0.514，0.52）。

以此类推，将这一过程归纳如图7-22所示。

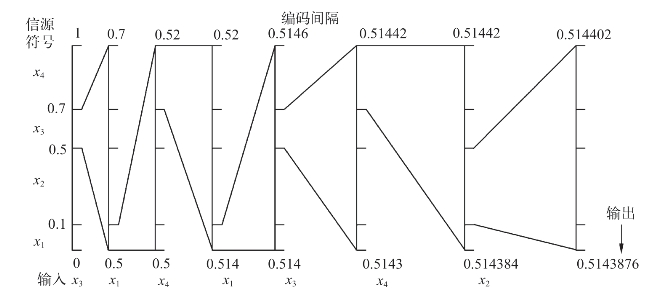
图7-22　算术编码举例

如果解码器也知道这一最后的范围［0.5143876，0.514402），它马上就可以解得第一个字符为x3，因为从各个符号的概率值及其所分配的编码区间范围看，只有x3的编码区间范围能包含［0.5143876，0.514402）。

在解码出x3后，范围变为［0.5，0.7），对所有符号再依据前面新区间表达式计算，并与最终范围［0.5143876，0.514402）比较看是否能包含它，不难解出第二个字符为x1，以此类推，解码器将唯一地解出这一串字符x3x1x4x1x3x4x2。

实际上对于解码器来说，不必要完全知道由解码器产生最终范围的两个端点，如上述例子中的0.5143876和0.514402，知道这一范围内的一个值已经足够了。

算术编码器对整个消息只产生一个码字，这个码字是在间隔［0，1）中的一个实数，因此译码器在接收到表示这个实数的所有位之前不能进行译码。

上述例子是基于概率统计的固定模式，实际应用中，不可能对大量的信息进行概率统计。算术编码的自适应模式弥补了这一不足。自适应模式中各个符号的概率初始值都相同，之后，信源符号的概率根据编码时符号出现的频繁程度动态地进行修改。

当信源符号概率比较接近时，算术编码的效率要高于Huffman方法。算术编码的缺点是：实现方法要比Huffman编码复杂一些，尤其是硬件实现。算术编码也是一种对错误很敏感的编码方法，如果有一位发生错误就会导致整个消息译错。