变换编码(Transform Coding)的基本思想是将在通常的欧几里德几何空间(空间域)描写的图像信号变换到另外的向量空间(变换域)进行描写,然后再根据图像在变换域中系数的特点和人眼的视觉特性进行编码。
正交变换编码系统框图如图7-14所示。

图7-14 变换编码系统框图
一般来说图像变换不是对整幅图像一次进行,而是在存储器中把一幅图像分成许多N×N的像块,然后依次将每个方块内的N×N个样点同时送入变换器进行变换运算。
变换器把输入的N×N点的像块由原空间域变换到变换域中,映射成同样大小的N×N点的变换系数矩阵,经过变换后的系数矩阵更有利于压缩。
量化器用有限个值来表示变换后的系数矩阵,通过量化器舍弃一些小幅度的变换系数。
4.编码器给量化器输出的每一个符号指定一个二进制码字,可以是定长码也可以是变长码。
(一)正交变换的性质
常用的正交变换有离散傅里叶变换(DFT)、最佳变换(KL)、离散余弦变换(DCT)及沃尔什变换(WH)等。
1.能量守恒性
可以证明图像在空间域中的数据平方和和图像在变换域中的数据的平方和存在能量守恒关系,即

2.能量集中性(Energy Compaction)
大部分正交变换趋向将图像的大部分能量集中到相对少数几个系数上,由于整个能量守恒,因此这意味着许多变换系数只含有很少的能量。
3.去相关性(Decorrelation)
当输入的像素高度相关时,变换系数趋向于不相关。
4.熵保持性
如果把f(x,y)看作是一个具有一定熵值的随机函数,那么变换系数F(u,v)的熵值和原来图像信号f(x,y)的熵值相等。
(二)一维离散余弦变换(Discrete Cosine Transform)
对于给定输入序列f(x),x=0,1,……,N-1,离散余弦变换定义为:

则DCT变换公式又可写为:

把a(u,x)展开则是一组余弦波,又称为基波分量。
以N=8的DCT变换为例,变换核函数为:
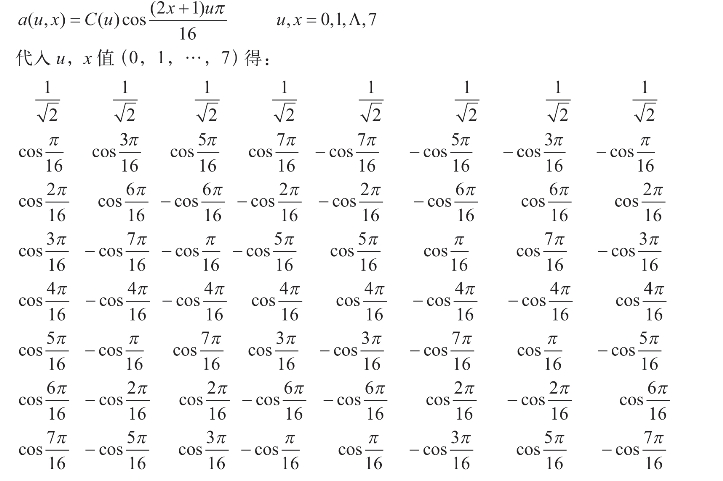
N=8的DCT基波向量如图7-15所示。

图7-15 N=8的DCT基波图
这八个基波中任意两个不同频率的基波对应样值相乘后的代数和都为0,相同频率的相乘后不为0,这也是正交变换的特性。
(三)二维DCT变换
二维DCT变换公式:
一个N×N像块f(x,y)(x,y=0,1,…,N-1)的二维DCT定义为:(https://www.xing528.com)

设变换核函数为:

则二维DCT变换公式又可表示为:

DCT基图像:
二维变换核函数a(x,y;u,v)按x,y,u,v分别展开后得到的是N×N个N×N点的像块组,又称为基图像。一个8×8的DCT基图像示意如图7-16所示。
其中,变量u表示基图像水平方向上的空间频率,v表示垂直方向上的空间频率。例如u=0和v=0对应的子像块是a(x,y,0,0),图像在x和y方向都没有变化,而u=7和v=7对应的子像块是a(x,y,7,7),图像在x和y方向的变化频率最高。

图7-16 8×8DCT基图像
二维DCT实际上是将空间像素的几何分布变换为空间频率分布,如图7-17 所示。

图7-17 空间域与变换域
计算举例:
一个8×8点的亮度像块如图7-18所示。

图7-18 DCT变换1
图中f(x,y)各点样值的幅度比较均匀,在空间域具有较大的相关性,经过DCT变换后,系数块F(u,v)中各点能量分布不均匀,主要集中在左上角低频区,其中直流系数F(0,0)具有最大值1260,而在高频区域大部分的F(u,v)都很小近似为0,体现了正交变换的能量守恒性、能量集中性、去相关性。
(四)量化器
为了压缩码率,还应该对变换域中的信号进行量化和编码。利用人眼对图像的低频分量比对高频分量更敏感的视觉特性,在低频区进行细量化,在高频区进行粗量化。
变换编码中的量化器是用降低系数的精度来消除不必要的系数,是在不降低预定图像主观评价质量条件下进行的。由于量化过程在变换域进行,因此设计量化特性应根据图像在变换域分布特性。以DCT变换为例,大多数电视信号如背景等部分亮度值变化很少,变换域中系数大部分能量集中在直流和低频区,又因为亮度突变区域如轮廓、边缘等部分较少,高频系数能量较小,如图7-19所示。

图7-19 DCT变换2
为了得到好的编码效果,应该根据系数块中的不同位置设计量化器。
以JPEG压缩算法为例,使F(u,v)中超过量化因子的系数值保留下来,可以表示为:
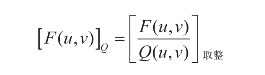
其中[F(u,v)]Q是系数F(u,v)的量化近似值,Q(u,v)是量化矩阵。将图7-18(b)中的系数块量化后如图7-20所示。

图7-20 DCT变换3
高频系数经过粗量化后,已经大部分为0,只有少数几个低频系数集中在左上角,大大压缩了数据量。
DCT编码中对图像会带来失真:
1.由于量化舍去高频系数而使图像产生模糊;
2.对某些系数采用粗量化而产生颗粒状结构;
3.像块的划分使相邻像块人为地造成亮度不连续,即块效应。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




