模拟信号的数字化过程及其步骤

模拟信号的数字化过程包括三步：取样、量化和编码，统称PCM编码，如图5-2所示：

图5-2　模拟信号的数字化框图

图5-2中，X（t）为模拟信号，fc为滤波器的截止频率，fs为取样频率，X（n）为数字信号。

取样是指用每隔一定时间的信号样值序列来代替原来在时间上连续的信号，也就是在时间上将模拟信号离散化。量化是指用有限个幅度值近似原来连续变化的幅度值，把模拟信号的连续幅度变为有限数量的有一定间隔的离散值。编码是指按照一定的规律，把时间、幅度离散的信号用一一对应的二进制或多进制代码表示的过程。

（一）连续时间信号的取样

对时间和幅度连续的模拟信号在时间轴上等间隔取样后，称为离散时间信号，其频谱与原模拟信号频谱相比发生了变化，如图5-3所示。

图5-3　离散时间信号频谱

设模拟信号为X（t），其频谱为X（f），模拟信号的带宽为fh，取样频率为fs，取样后的离散时间信号为X'（t），其频谱为X'（f），可以证明X'（f）是一个周期函数，是以原模拟信号X（t）的频谱X（f）的周期延拓形成的，周期为取样频率fs。

X'（f）与X（f）的关系为：

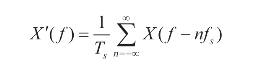
式中，n为整数，Ts为取样周期：Ts=1/f s。

由图5-2可知：

1.取样后的离散时间信号的频谱X'（f）是原模拟信号的频谱X（f）以取样频率 fs为周期延拓形成的。

2.若取样频率fs足够大，取样后的离散时间信号的频谱X'（f）不会发生混叠，否则会发生混叠。

3.取样后的离散时间信号的频谱X'（f）不会发生混叠的条件是：fs≥2fh，即取样频率应大于或等于原模拟信号带宽的2倍，称为取样定理。

4.如果取样频率满足取样定理，将取样后的离散时间信号通过一个截止频率为fs/2的理想低通滤波器，就能够恢复原模拟信号。

在对模拟信号取样前，要先通过一个低通滤波器，将高于fc的高频分量滤除。由于低通滤波器的截止边缘不可能像理想滤波器那样陡峭，因此实际上取样频率fs应比2fh大很多。

（二）离散时间信号的量化

取样后的离散时间信号在幅度上仍是连续的，即每一个样值有无限多个可能的电平取值。要精确地表示每一个样值的大小需要无限多位二进制数，这是不可能也是没必要的。因为电视显像管和人的视觉特性无法区分无限小的亮度变化值，所以需要对离散时间信号进行幅度量化。

量化就是把幅度连续变化的信号变换为幅度离散的信号，按量化对象不同，可分为标量量化和矢量量化，按量化间隔是否均匀，又可分为均匀量化和非均匀量化。标量量化是一维的量化，一个幅度对应一个量化结果。矢量量化是二维甚至多维的量化，两个或两个以上的幅度决定一个量化结果。均匀量化是量化器的输入动态范围被均匀地划分为2n份，均匀量化的好处就是编解码很容易，但要达到相同的信噪比占用的带宽要大。现代通讯系统中都用非均匀量化，非均匀量化是根据信号的不同区间来确定量化间隔的。对于信号取值小的区间，其量化间隔也小；反之，量化间隔就大。

1.均匀量化原理

设输入信号的动态范围为A，每一个量化间隔为ΔA，量化分层级数为M，M=2n，n称为量化比特数，则A=M×ΔA=2n×ΔA，M和n的取值决定量化信噪比。

量化结果为阶梯波，如图5-4所示。

图5-4　均匀量化

图中，A=1，M=8，n=3，ΔA=0.125。

设输入的连续信号为X（t），输出的阶梯信号为Y（t），则e（t）=X（t）-Y（t）称为量化误差。当信号量化处理时，量化误差e（t）的范围为+ΔA/2～-ΔA/2。

由于量化误差会使恢复图像出现颗粒状细斑，因而量化误差又称为颗粒噪声或量化噪声。如果信号的功率密度谱为均匀分布函数，则可以证明，量化噪声功率为：

量化间隔ΔA越小，量化误差就越小，量化噪声也越小。

2.量化信噪比

单极性信号量化信噪比与双极性信号量化信噪比不同。

（1）单极性信号量化信噪比

单极性信号（如视频信号）量化信噪比一般用信号峰-峰值与量化噪声有效值之比表示为：

(www.xing528.com)

用分贝表示为：

量化比特数n每增加1比特，量化信噪比上升6dB。在数字电视中，常用的量化比特数为8、9、10。

量化比特数n越大，量化信噪比越高，量化噪声也越小，量化比特数n对图像的影响如图5-5所示。

4bit量化和8bit量化的结果如图5-6所示。

图5-6中，4bit量化的图像比较粗糙，有块状斑痕；8bit量化的图像看不到块状斑痕。

图5-5　量化比特数n对图像的影响

图5-6　4bit量化和8bit量化

（2）双极性信号（如声音信号）量化信噪比

设双极性信号的最大幅度为A，动态范围是+A～-A，对它均匀量化成M级，则有：

2A=M×ΔA=2n×ΔA

其中，n为量化比特数。

量化信噪比用信号功率与量化噪声功率之比表示为：

量化信噪比

用分贝表示为：

若输入信号幅度为a，小于最大输入幅度A，则量化信噪比又可表示为：

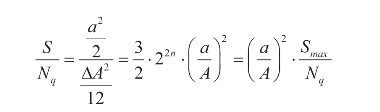
用分贝表示为：

当输入信号幅度下降1/2时，信噪比将下降6dB。在数字电视中，常用的音频信号的量化比特数有16bit、20bit和24bit等几种。

可见，单极性信号与双极性信号的量化比特数不同。

（3）量化噪声对图像的影响

量化噪声对图像的影响主要有以下几方面：颗粒杂波、伪轮廓、边缘忙乱。

（三）编码

量化器输出的信号是用十进制表示的离散电压信号，为使电路能够实现还要转换为二进制代码。

在PCM编码中，一般采用二进制等长码，即每一量化等级都用相同位数n的二进制码表示，n位二进制码有2n种排序，用其中一种排序表示一个量化级。

按码元的排列不同，等长二进制码有多种，在数字电视中常用自然二进制码、格雷码、折叠码等代码，如表5-1所示。

表5-1　三种等长二进制码

自然二进制码逢二进一，优点是编译码简单、直观，获得了广泛应用，缺点是相邻码字的对应码元不同的个数（称为码距）多，译码中发生错误的可能性大。

格雷码又称为交替二进制码，是由自然二进制码演变而来的，编译码不容易发生错误。格雷码的第i位gi是由自然二进制码的第i位bi及高一位bi+1模2加而得的，即：

折叠码也是由自然二进制码重排而成的，它的高位码元（MSB）代表信号的正负极性，0代表正值，1代表负值。其他各位都以某一中心值作上下对称分布，即中心值上下两部分各位成“倒影”关系，这就是折叠之意，适合声音信号编码（双极性信号）。

2的补码与折叠二进制码类似，适用于双极性信号。首位代表极性，其他各位按代数值从大到小。对于正值，和折叠二进制码相同，对于负值，两者的码字次序相反。