基于模拟退火算法的小麦粉品质近红外光模型优化方法

模拟退火算法是S.Kirkpatrick等人在1983年提出的，其基本思想来源于金属的退火原理。将材料加热，材料能量变大，原子离开原始位置随机在其他位置移动，再冷却材料使其能量减少，如果冷却速度足够慢，系统会忽略局部稳定构造，最后在常温时达到全局稳定状态，即基态。模拟退火算法较其他优化算法有如下特点：

1）初始点选择的不依赖性，对于随机搜索算法这是十分重要的优势，避免了因初始点选择不当造成的优化失败。

2）以一定概率接受劣解，保证算法不陷入局部最优且增加了寻优灵活性。

3）隐含并行性，模拟退火算法采用并行策略，优化提高了收敛速度和解的质量。

4）善于搜索复杂区域。

模拟退火算法在很多优化问题上都有应用。石吉勇等人基于模拟退火算法优化食醋总酸含量近红外光谱模型，优选出17个总酸特征波数点，其预测集相关系数为0.921优于全光谱和iPLS法对应的预测效果。石吉勇等人还将模拟退火算法应用于检测草莓坚实度模型的波长优化，并结合了多种光谱预处理方法，实验结果表明模拟退火算法可以提高近红外模型预测草莓坚实度的准确度和稳健性。Roman M.Balabin等人对比16种优化光谱区算法对生物柴油特征的提取结果，得出模拟退火算法是优化效果明显的算法之一。

1.算法原理

近红外光谱的2074个波数点相当于退火材料的2074个微观状态。选定目标函数f即材料的内能E，确定优化问题的初始温度T₀，随机选择一组波数作为模拟退火的初始解，由初始温度和初始解开始迭代。迭代过程如下：产生新的解，然后计算其目标函数差，如果新的目标函数优于前一解的目标函数，则算法接受并更新最优解。否则，由接受准则判断是否接受这个解，满足则进行当前解和目标函数的迭代，否则舍弃新解。随着迭代的过程，逐步衰减温度值T。当温度为T_x时所经历的迭代过程为一个马尔科夫链，次数为马尔科夫链的长度L_k。算法设置了记忆器，用于记忆当前迭代过程中遇到的最优解和最优目标函数值，防止问题具有多个极值时，算法难以保证最优解为整个搜索过程中曾经得到的最优解。最终，算法终止时得出的历史最优解，即优选的波数点。

（1）接受准则

接受准则保证了模拟退火算法在一定程度上吸收劣解，是实现全局搜索的关键因素。经试验表明，接受准则的具体形式对模拟退火算法没有实质性的影响，所以通常选用Metropolis准则作为接受准则函数。

由解i到解j的接受概率由以下函数确定：

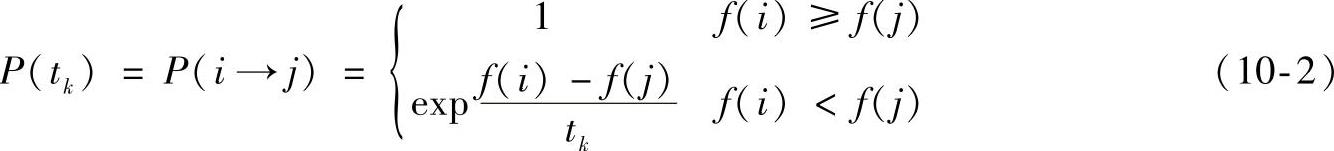
式中，f（i）、f（j）分别表示解i、j的目标函数；t_k表示温度。

依据接受准则可以看出，目标函数越小越好。

（2）目标函数

目标函数的选择在一定程度上会影响实验结果，常用的目标函数主要是RMSECV、RMSEP以及相关系数R²。

（3）冷却进度表

冷却进度表是模拟退火算法控制进程的参数总称，包括初始温度T₀、衰减因子α、马尔科夫链长度L_k以及终止条件S。理论上初始温度T₀遵循足够大原则才能保证算法能够进行大范围搜索，但实际情况需考虑T₀过大会降低模拟退火算法优化计算的时间。降温策略选择指数降温T_k+1=T_kα。衰减因子α越小所需的马尔科夫链越长，因此通常选取小衰减量来避免。终止条件S为温度降到一个接近0的数值。

2.算法流程（见图10-16）

3.实验结果

（1）小麦粉中水分含量的SAA-PLS定量模型

采用水分浓度区间为10%～16%的校正样本建立全谱PLS定量分析模型，并结合光谱预处理以及模拟退火算法优化该模型，各方法优化结果见表10-11。

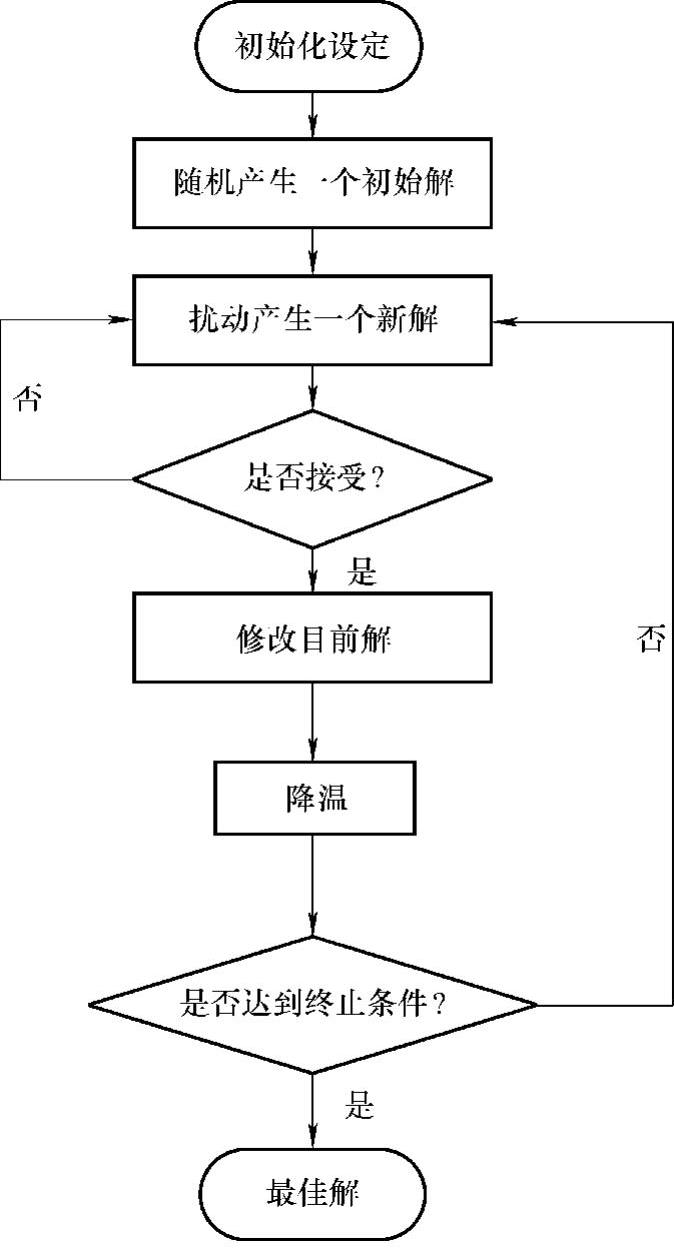
图10-16 模拟退火算法流程

表10-11 光谱预处理结合模拟退火算法优化模型结果（水分）

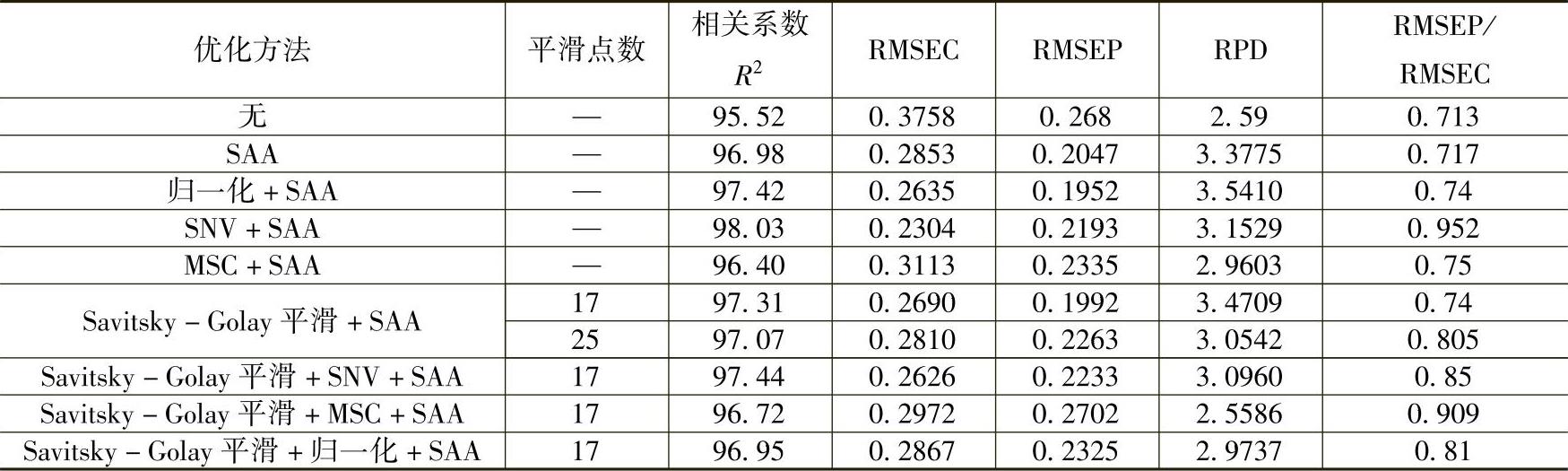
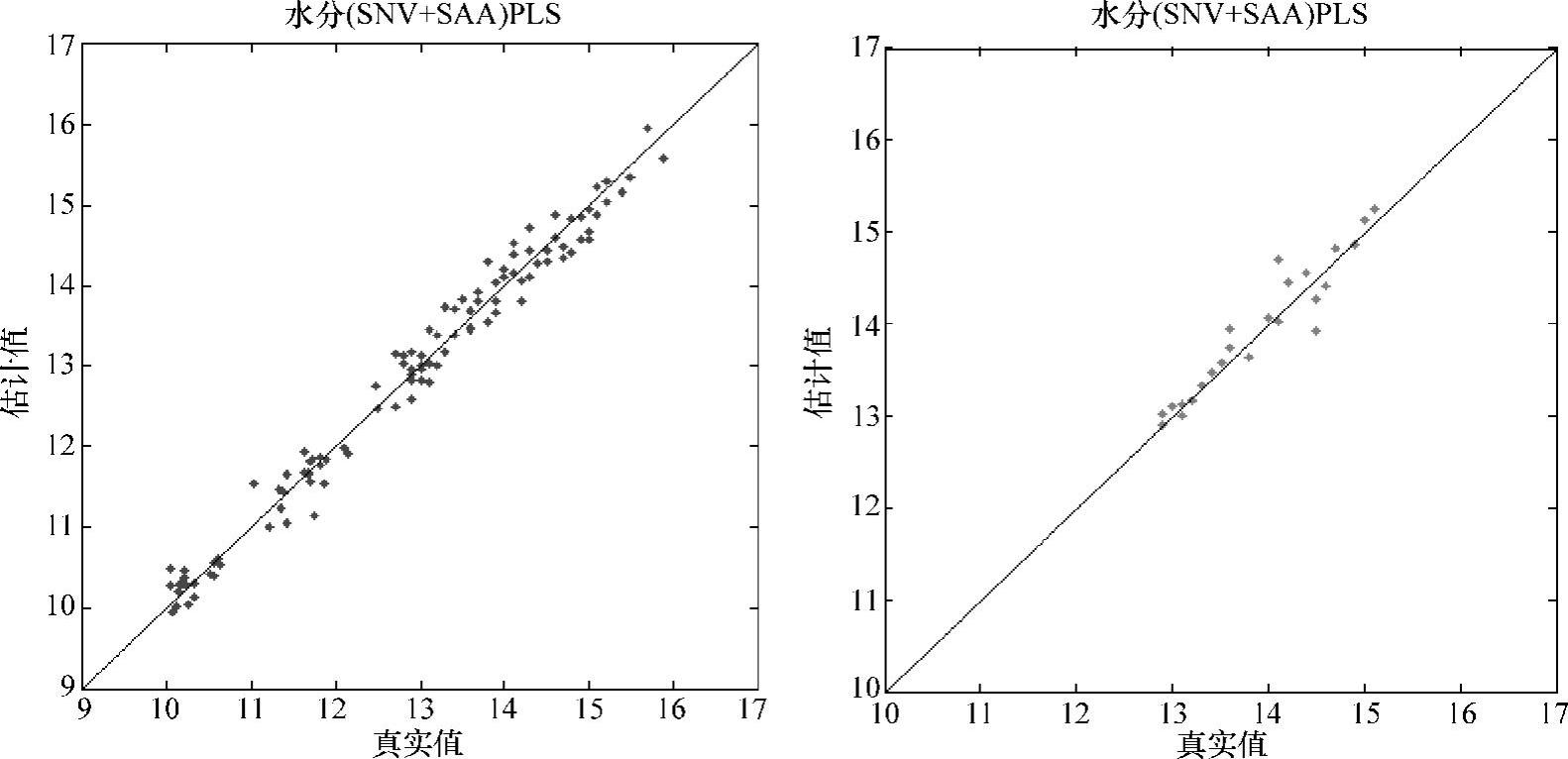
从优化结果可以看出，模拟退火算法优化波长后，模型的预测准确度明显提高，说明结合相应算法优化波长是有效且必要的。除MSC和Savitsky-Golay平滑+MSC法结合模拟退火算法优化效果一般外，其余预处理方法结合模拟退火算法效果均优于仅筛选波长优化定量模型的结果，其中综合对比各指标参数值，归一化光谱预处理方法结合模拟退火优化波长优化模型效果最好，模型相关系数R²为97.42，RMSECV为0.2635，RMSEP为0.1952，波数由2074个点筛选为49个点，定量分析模型校正集与检验集如图10-17所示：

(www.xing528.com)

图10-17 SNV结合SAA-PLS定量模型

归一化结合模拟退火算法优化模型的检验集样本真实值与估计值误差见表10-12。

表10-12 检验集样本真实值与估计值误差

（2）小麦粉中灰分含量的SAA-PLS定量模型

将灰分全谱PLS定量模型采用各光谱预处理方法以及模拟退火算法优化模型，各方法优化结果见表10-13。

表10-13 光谱预处理结合模拟退火算法优化模型结果（灰分）

从优化结果可以看出，光谱预处理集合模拟退火算法优化模型预测结果明显优于无任何处理的PLS定量分析模型，归一化、Savitsky-Golay平滑、Savitsky-Golay平滑+SNV、Savitsky-Go-lay平滑+MSC以及Savitsky-Golay平滑+归一化预处理方法结合模拟退火算法结果较好，SNV和MSC效果略差。综合考虑模型准确度与稳健性，Savitsky-Golay平滑+SNV预处理结合模拟退火算法优化灰分含量PLS定量模型效果最好，模型相关系数R²为98.32，RMSECV为0.0184，RM-SEP为0.0138，波数由2074个点筛选为49个点，定量分析模型校正集与检验集如图10-18所示。

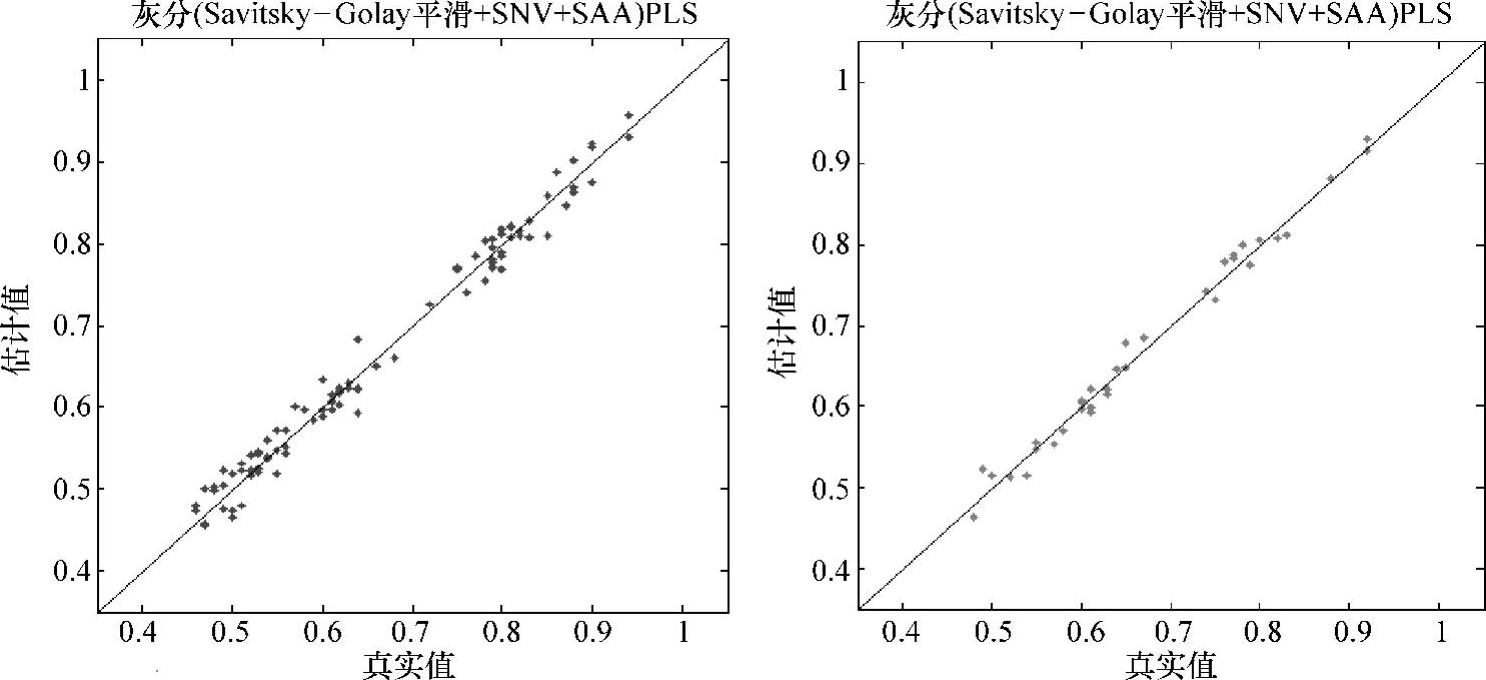
图10-18 Savitsky-Golay平滑+SNV-PLS定量模型

Savitsky-Golay平滑+SNV结合模拟退火算法优化模型的检验集样本真实值与估计值误差见表10-14。

表10-14 检验集样本真实值与估计值误差

（3）小麦粉中湿面筋含量的SAA-PLS定量模型

将湿面筋全谱PLS定量模型采用各光谱预处理方法以及模拟退火算法优化模型，各方法优化结果见表10-15。

表10-15 光谱预处理结合模拟退火算法优化模型结果（湿面筋）

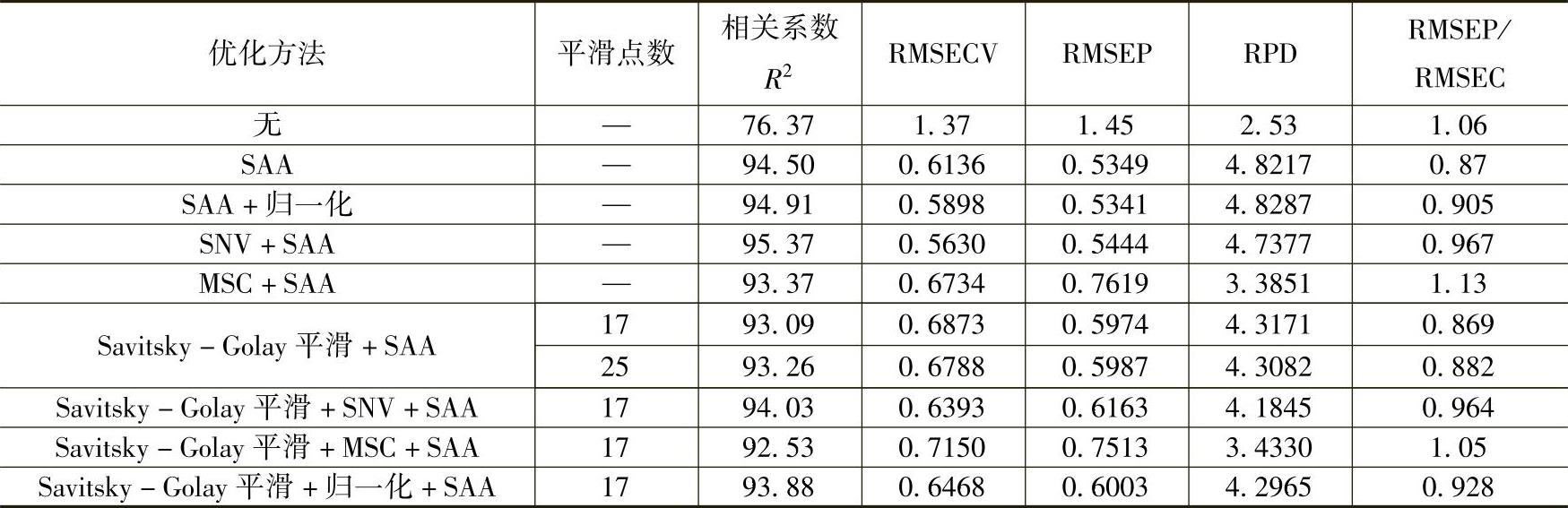
从表10-15中可以看出，经模拟退火算法优化波数后，模型的预测准确度明显提升，其中结合SNV预处理方法的优化模型实验结果最好，结合归一化预处理方法的优化模型次之，结合MSC、Savitsky-Golay平滑以及Savitsky-Golay平滑+MSC效果最差。SNV结合模拟退火算法建立的湿面筋PLS定量模型相关系数R²为95.37，RMSECV为0.563，RMSEP为0.5444，RPD为4.7377，波数由2074个点筛选为80个点，所建定量分析模型校正集与检验集如图10-19所示。

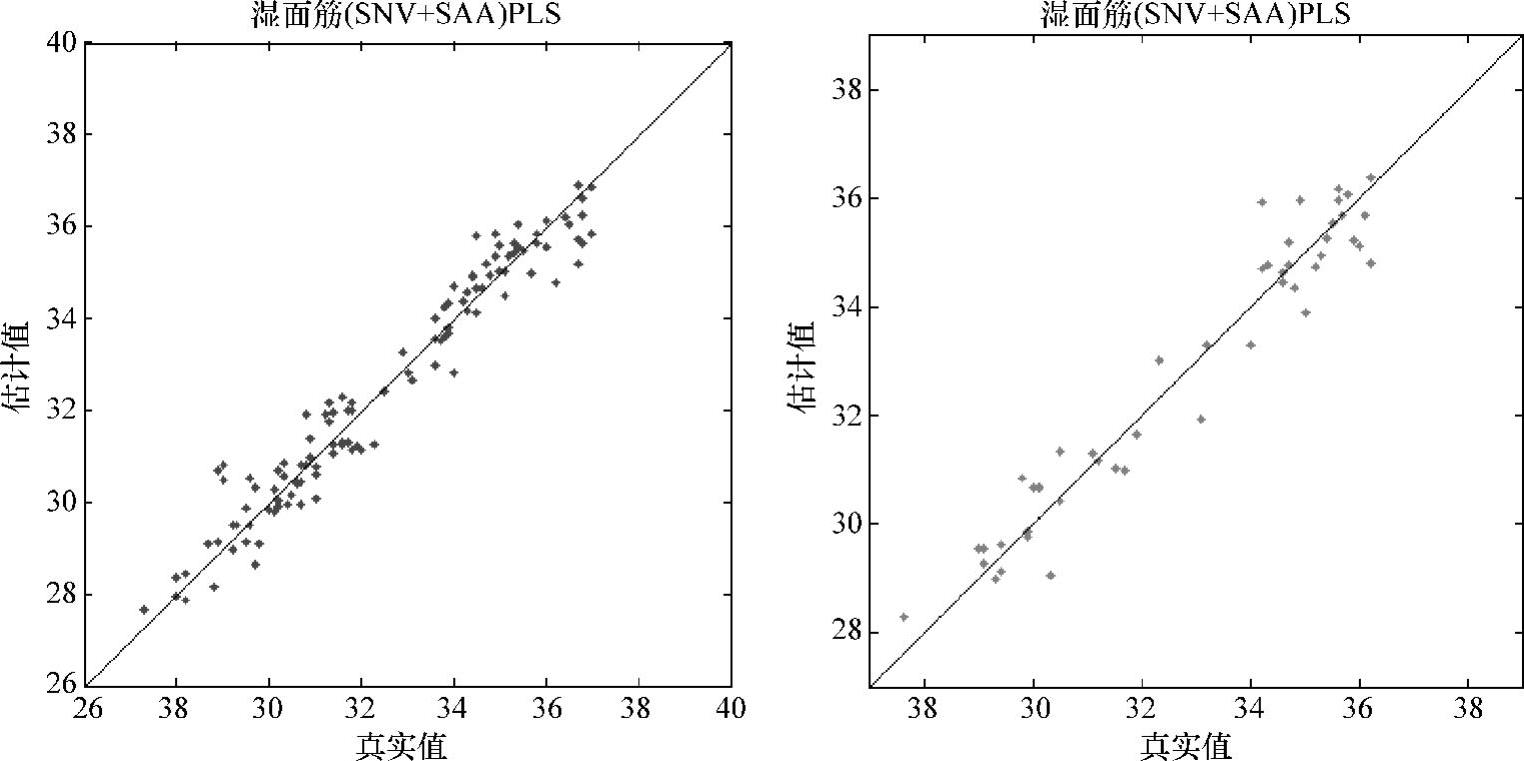
图10-19 SNV+SAA湿面筋PLS定量模型

SNV结合模拟退火算法优化模型的检验集样本真实值与估计值误差见表10-16。

表10-16 检验集样本真实值与估计值误差

所有的优化模型RMSEP均没有达到国家针对近红外光谱检测小麦粉中粗蛋白RMSEP要低于3%的要求，主要原因在于使用小麦粉中湿面筋含量估计粗蛋白含量还是存在一定误差，导致模型准确度略低。

从小麦粉中水分、灰分以及湿面筋3个PLS定量模型来看，光谱预处理方法结合模拟退火筛选波长来优化PLS定量分析模型可行且预测效果明显优于原模型，预测精度也高于遗传算法优化定量模型，但模拟退火算法优化时间略长。由于优化方法使用MATLAB编程，方便嵌入各种光谱分析设备，只要调整相关参数便可优化光谱数据及模型，十分方便。