基于遗传算法的小麦粉品质近红外光模型优化方法研究

光谱采用多元校正方法（如PLS法）分析时，传统观点认为校正方法具有较强的抗干扰能力，可以全光谱信息进行建模分析。但随着研究的不断深入和应用问题的复杂化，研究人员通过对样本光谱波长或波长区间按一定方法进行筛选，可能会得到结果更好的校正模型。波长的优化不仅减少了参与校正方法计算的波长点数，降低了数据运算时间，还提高了检测工作的效率。并且由于剔除了无用信息或非线性变量，校正模型的预测能力和稳健性会有一定程度的提高。

1.基于遗传算法的波长优化方法介绍

遗传算法（Genetic Algorithms，GA）是20世纪60年代由美国密歇根大学的John Holland教授提出的，它来源于生物界中的自然选择和遗传机制，通过优胜劣汰的方式选择最优的结果。遗传算法主要利用选择（Selection）、交叉（Crossover）和变异（Mutation）等操作，经迭代过程挑选出可以优化目标函数值的变量，剔除较差的变量，来实现问题的优化。遗传算法具有以下特征：

1）具有自组织、自适应能力的全局搜索算法。

2）实际问题参数需通过一定方法编码转化为遗传空间的基因型串结构数据。

3）搜索结果优劣基于目标函数的评价信息，避免优化过程受制于数学运算。

4）具有隐含并行性。遗传算法的优化过程是种群并行搜索的过程。

5）算法基本思想简单，具有优化过程简单通用、稳健性强等优势。但在局部搜索方面欠佳，容易出现早熟现象。

遗传算法在很多问题上均有应用。如刘辉军等人利用遗传算法优化绿茶水分和氨基酸的近红外光分析模型，实验结果表明优化后模型稳健性增强，水分和氨基酸预测集方均根误差分别减小了76.6%和82.1%。

屠振华等人将遗传算法结合iPLS法应用于苹果硬度检测模型中，不但降低了模型的复杂度，同时提高了模型的预测准确度。陈红艳等人通过遗传算法优化高光谱波长，建立潮土碱解氮定量分析模型同样取得了较好的实验结果。

遗传算法实现流程如图10-3所示。

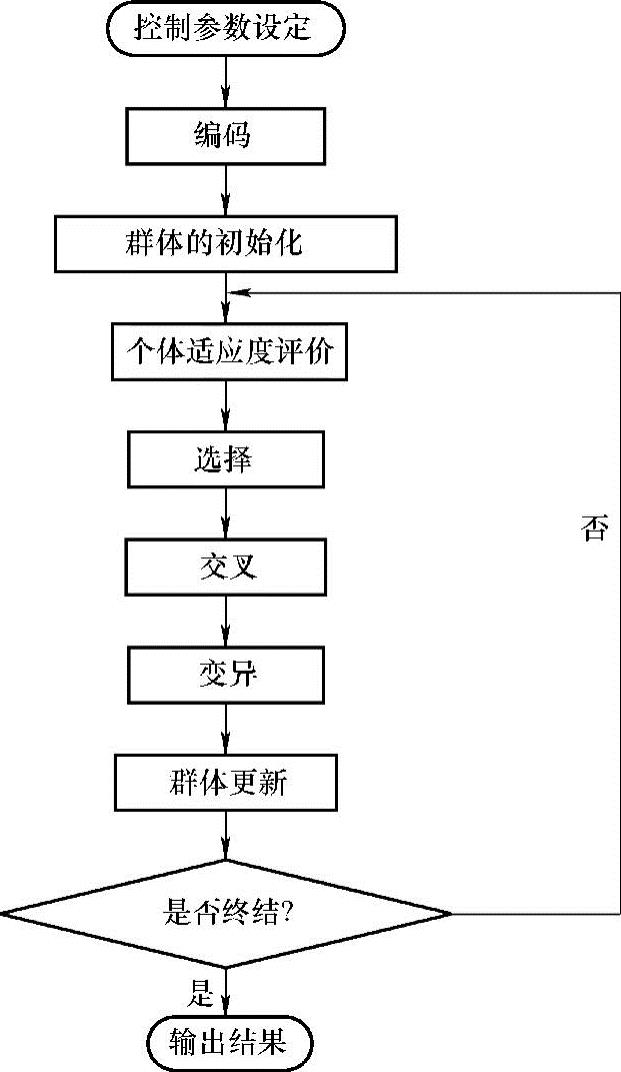
图10-3 遗传算法实现流程

2.基于GA-PLS法的小麦粉水分定量模型建立与分析

实验在建立基于遗传算法优化波长的小麦粉中水分含量PLS定量模型时，种群规模设定为30，最大迭代次数设定为150，提取特征波长数量为60，适应度函数选择RMSEP：

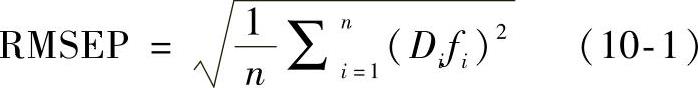
式中，D_if_i=x_i-y_i为第i个样本测定值x_i参比值y_i之差。

遗传算法适应度函数收敛结果如图10-4所示，遗传算法在迭代150次时适应度函数已经趋于平稳，特征波长数量随模型相关系数R²和RM-SEC的变化如图10-5所示，算法在特征波长数量为60时趋于平稳。

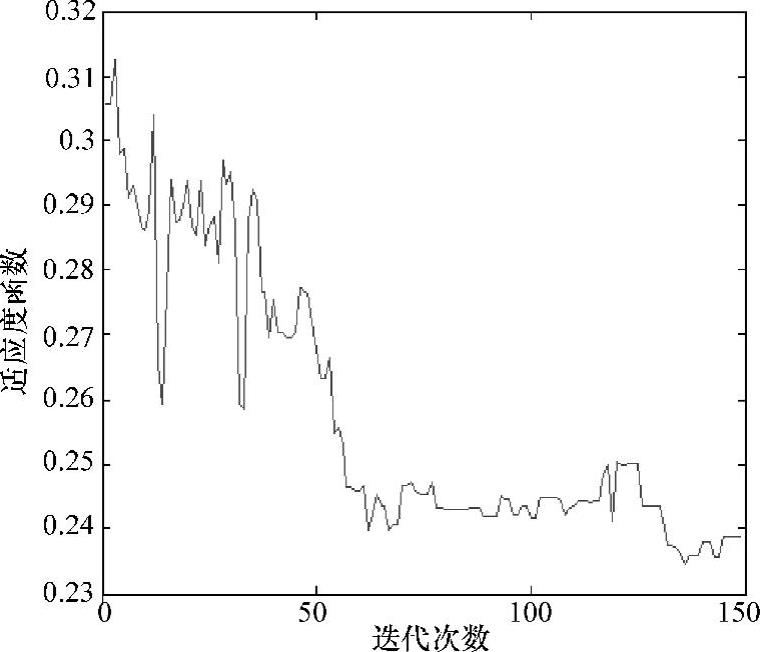
图10-4 适应度函数随迭代次数收敛结果

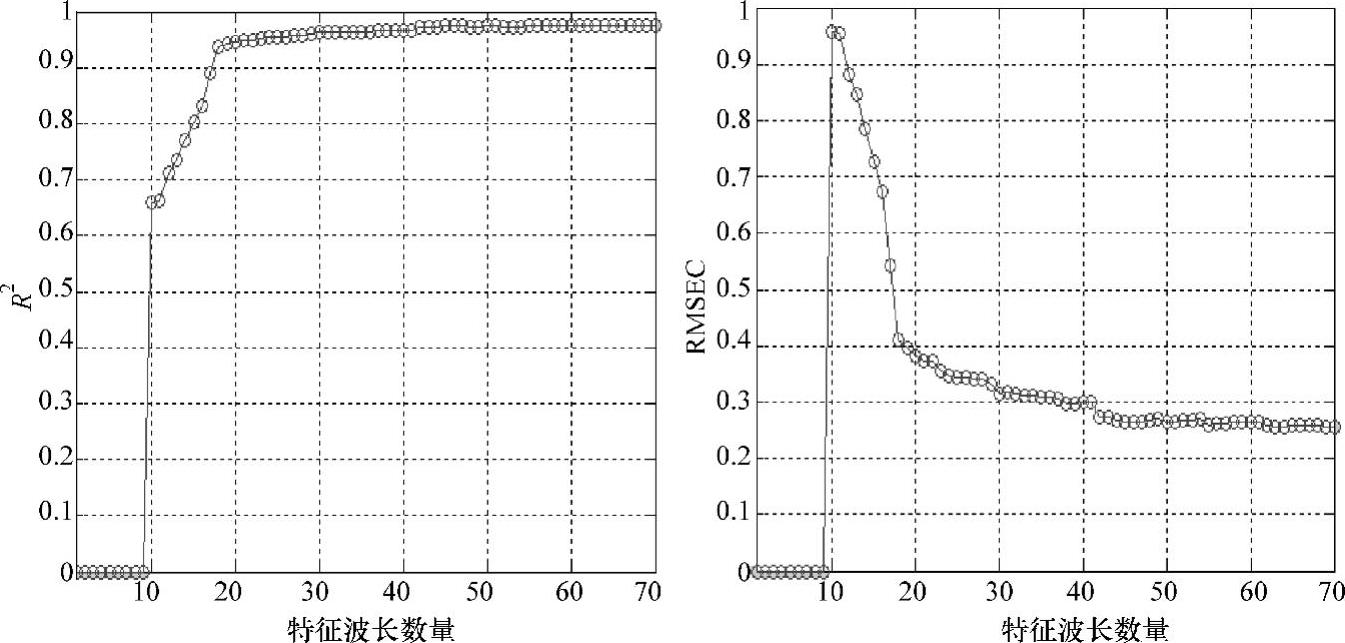
图10-5 特征波长数量随模型相关系数R²和RMSEC的变化

采用水分含量区间为10%～16%的校正样本建立全谱PLS定量分析模型，并结合光谱预处理以及遗传算法优化该模型，各方法优化结果见表10-5。

表10-5 光谱预处理结合遗传算法优化模型结果（水分）

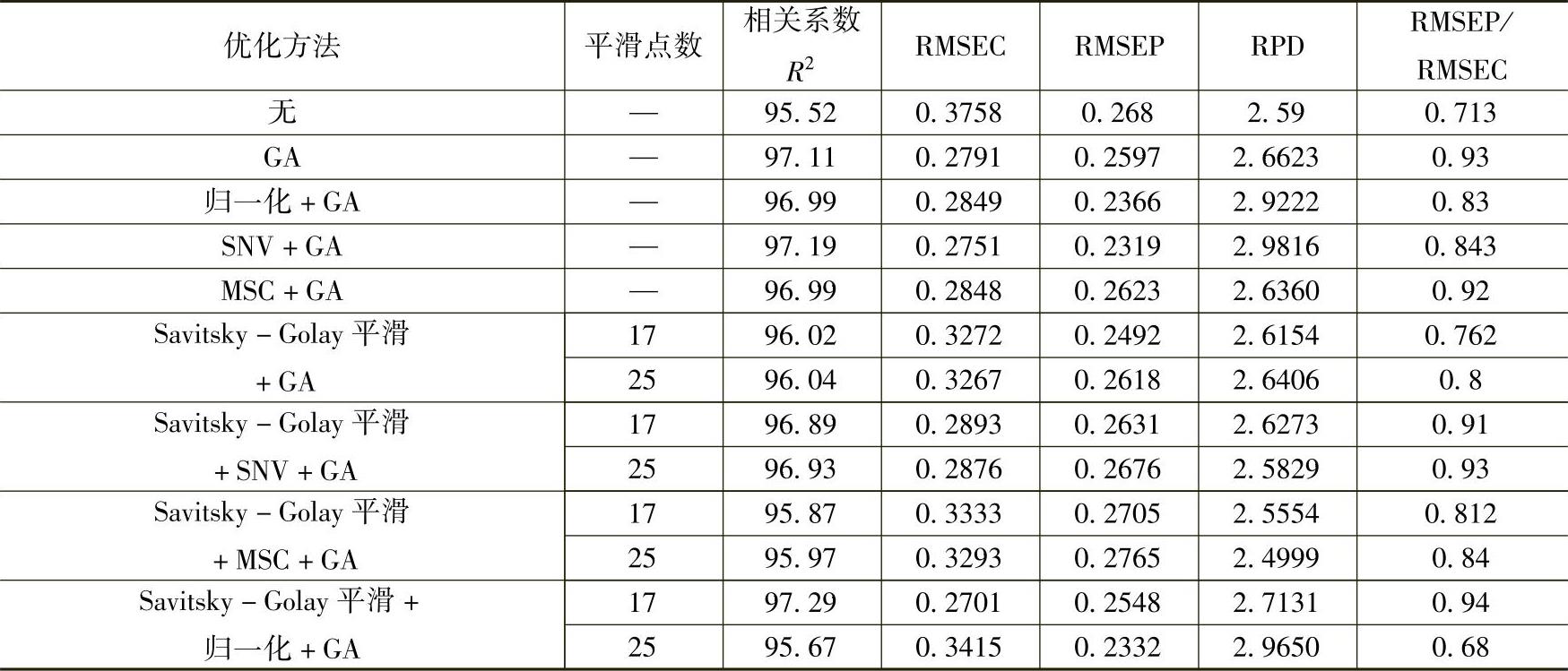
从实验结果得出，遗传算法筛选特征波长可以有效提升模型的预测准确度和稳健性，结合适合的光谱预处理方法后，模型的优化结果进一步得到提升。其中SNV和Savitsky-Golay平滑+归一化与遗传算法相结合后模型的预测准确度最好，并且RPD结果较好，属于可接受范围内，模型稳健性良好。其余预处理方法与遗传算法相结合优化模型预测准确度都有所提升，模型稳健性良好。

光谱经SNV法预处理后光谱图如图10-6所示。SNV结合遗传算法优化的水分PLS定量分析模型如图10-7所示。

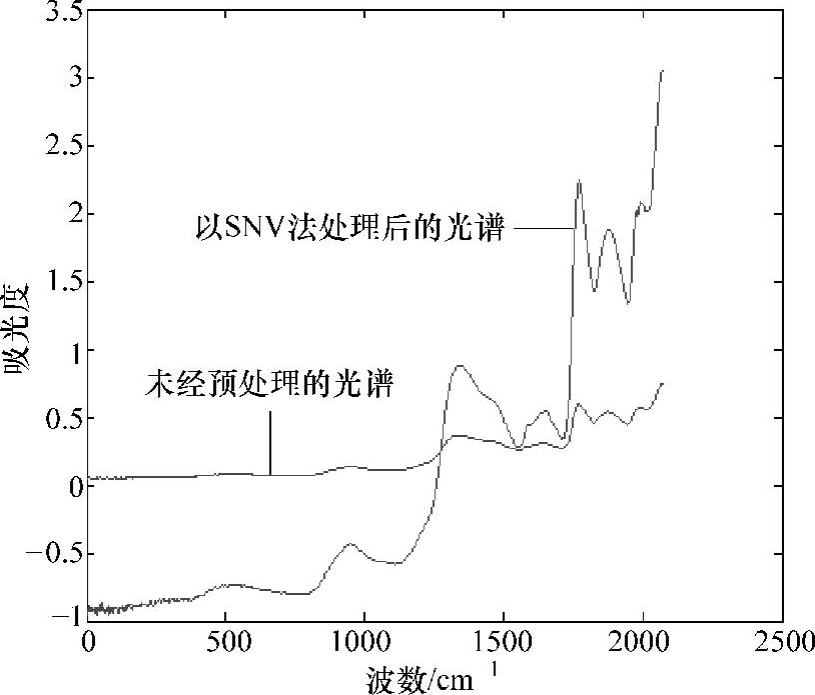
图10-6 SNV法预处理后的光谱图

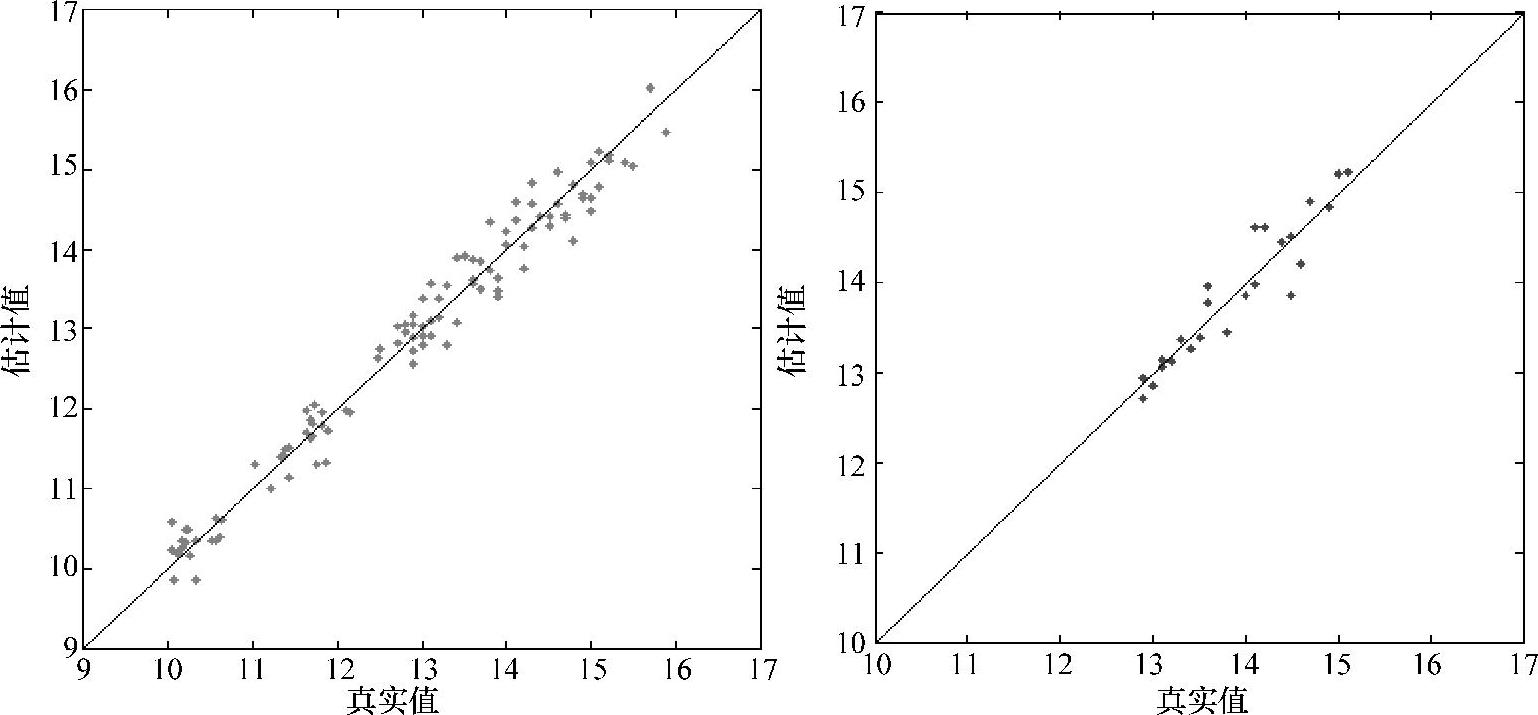
图10-7 SNV+GA的水分PLS定量模型

SNV结合遗传算法优化模型的检验集样本真实值与估计值误差见表10-6。

表10-6 检验集样本真实值与估计值误差

3.基于GA-PLS法的小麦粉灰分定量模型建立与分析

建立关于灰分含量的全谱PLS定量校正模型，并对检验集样本进行预测。模型预测结果如图10-8所示。

灰分含量全谱PLS定量模型实验结果：相关系数R²为70.31，RMSEC为0.0775，RMSEP为0.0914，RPD为1.345，RMSEP/RMSEC为1.18。由结果看出，取全谱波数建立PLS定量模型，实验结果预测准确度差，且模型稳健性不高。

实验在建立基于遗传算法优化波长的小麦粉中灰分含量PLS定量模型时，种群规模设定为30，最大迭代次数设定为150，提取特征波长数量为80，适应度函数选择RMSEP。

特征波长数量随模型相关系数R²和RMSEC的变化如图10-9所示，算法在特征波长数量为80时趋于平稳。

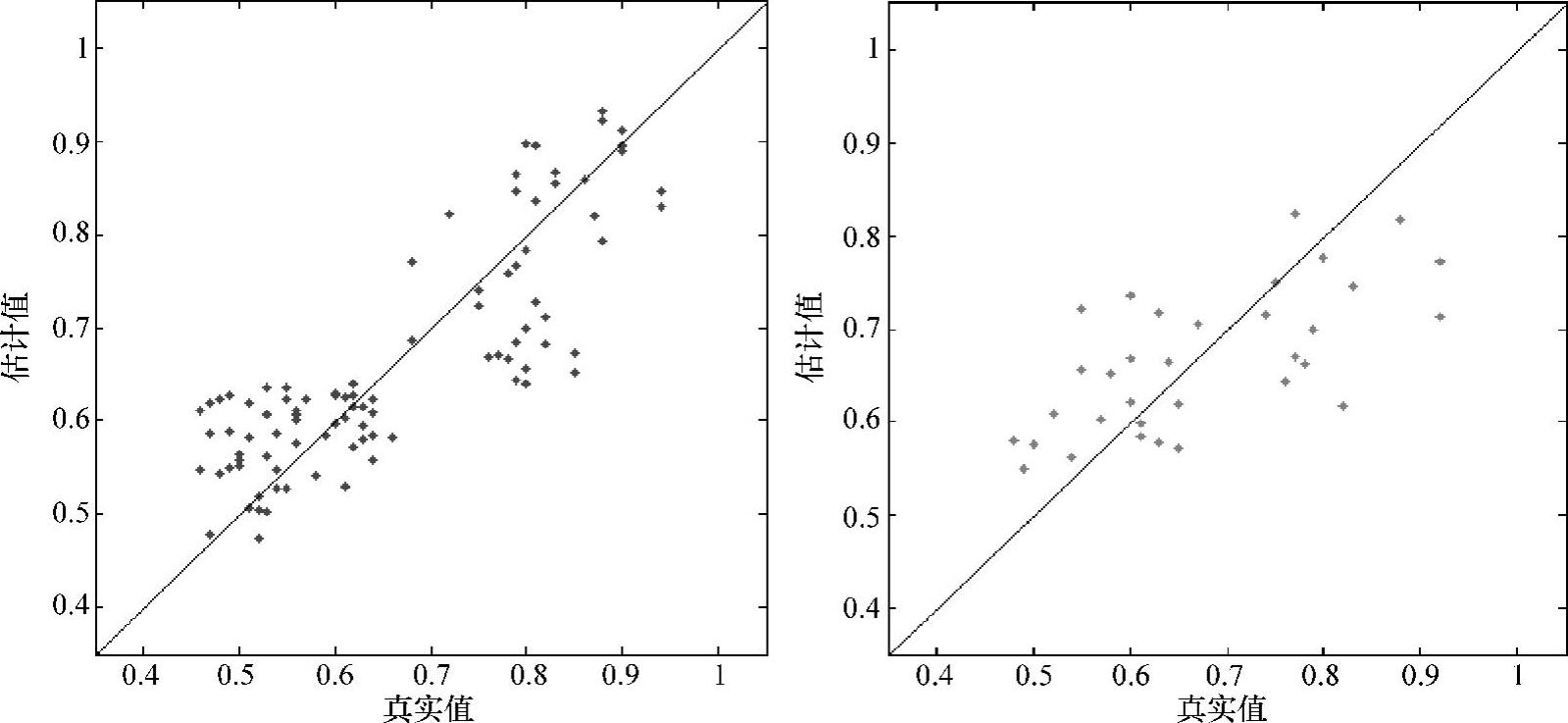
图10-8 灰分的全谱PLS定量模型(www.xing528.com)

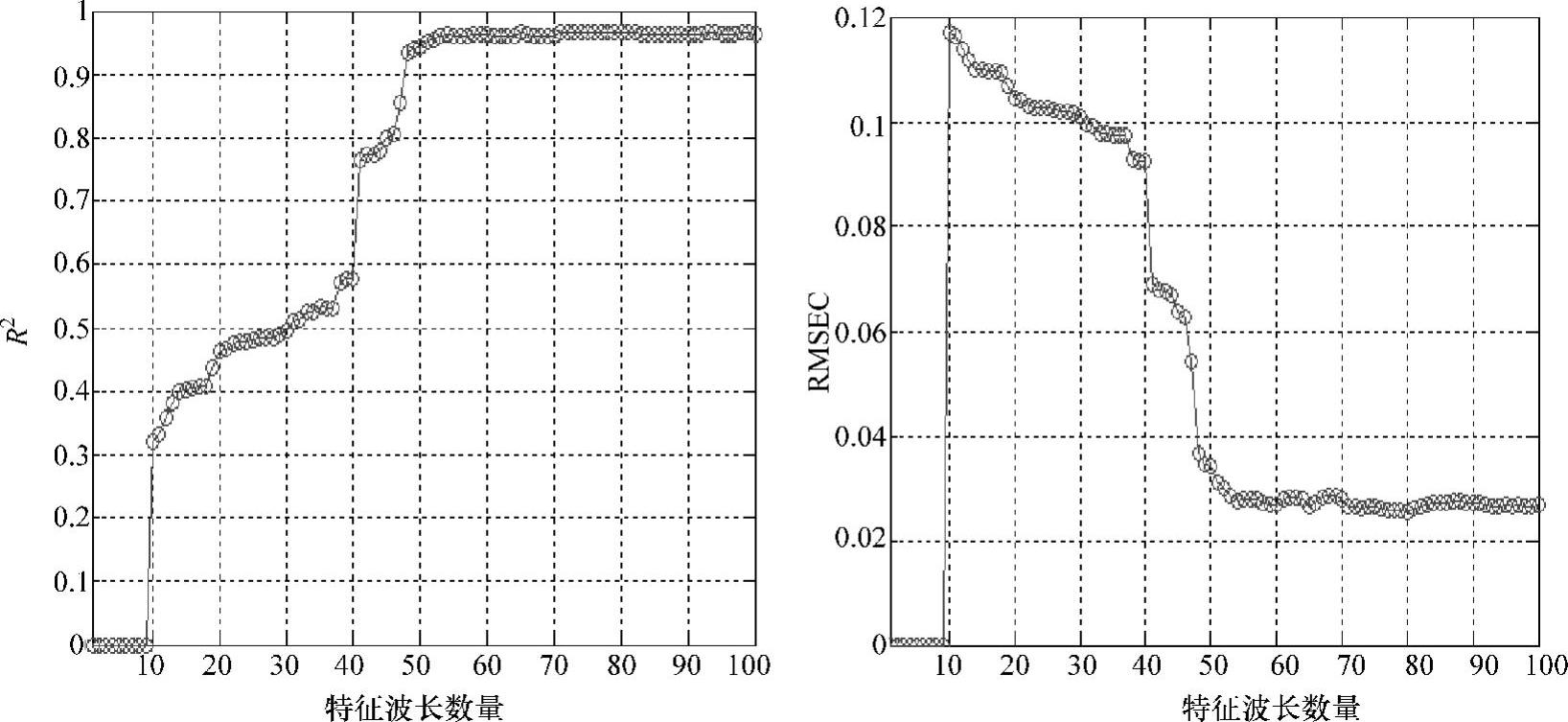
图10-9 特征波长数量随模型相关系数R²和RMSEC的变化

将灰分全谱PLS定量模型采用各光谱预处理方法以及遗传算法优化模型，各方法优化结果见表10-7。

表10-7 光谱预处理结合遗传算法优化模型结果（灰分）

（续）

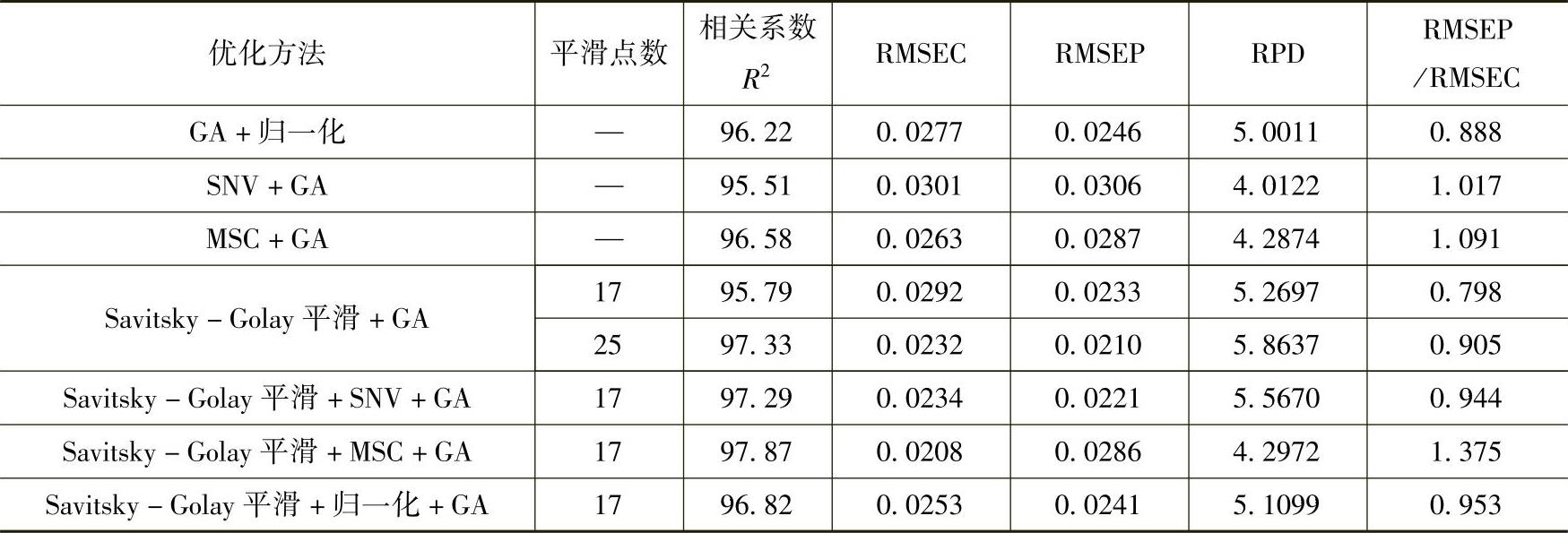
从实验结果看，模型经遗传算法筛选特征波长后，预测准确度有了大幅提高，并且结合适合的光谱预处理方法后，模型得到了更完整的优化。根据模型的准确度与稳健性参数，Savitsky-Golay平滑（25）点结合遗传算法优化模型结果最为理想，相关系数R²为97.33，RMSEC为0.0232，RMSEP为0.021，RPD达到5.8637，模型稳健性良好。

光谱经Savitsky-Golay平滑（25）预处理后光谱图如图10-10所示。

Savitsky-Golay平滑（25）结合遗传算法优化的灰分PLS定量分析模型如图10-11所示。

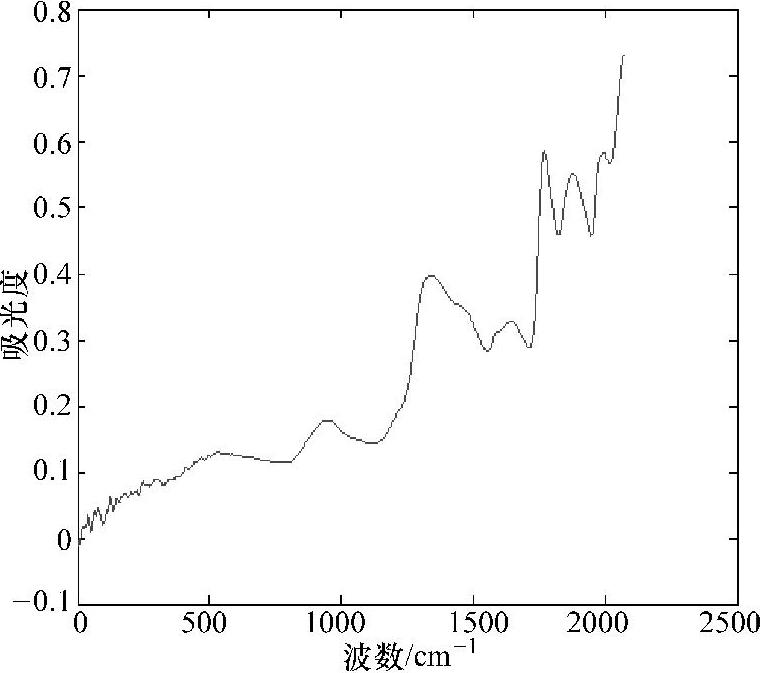
图10-10 Savitsky-Golay平滑（25）预处理后的光谱图

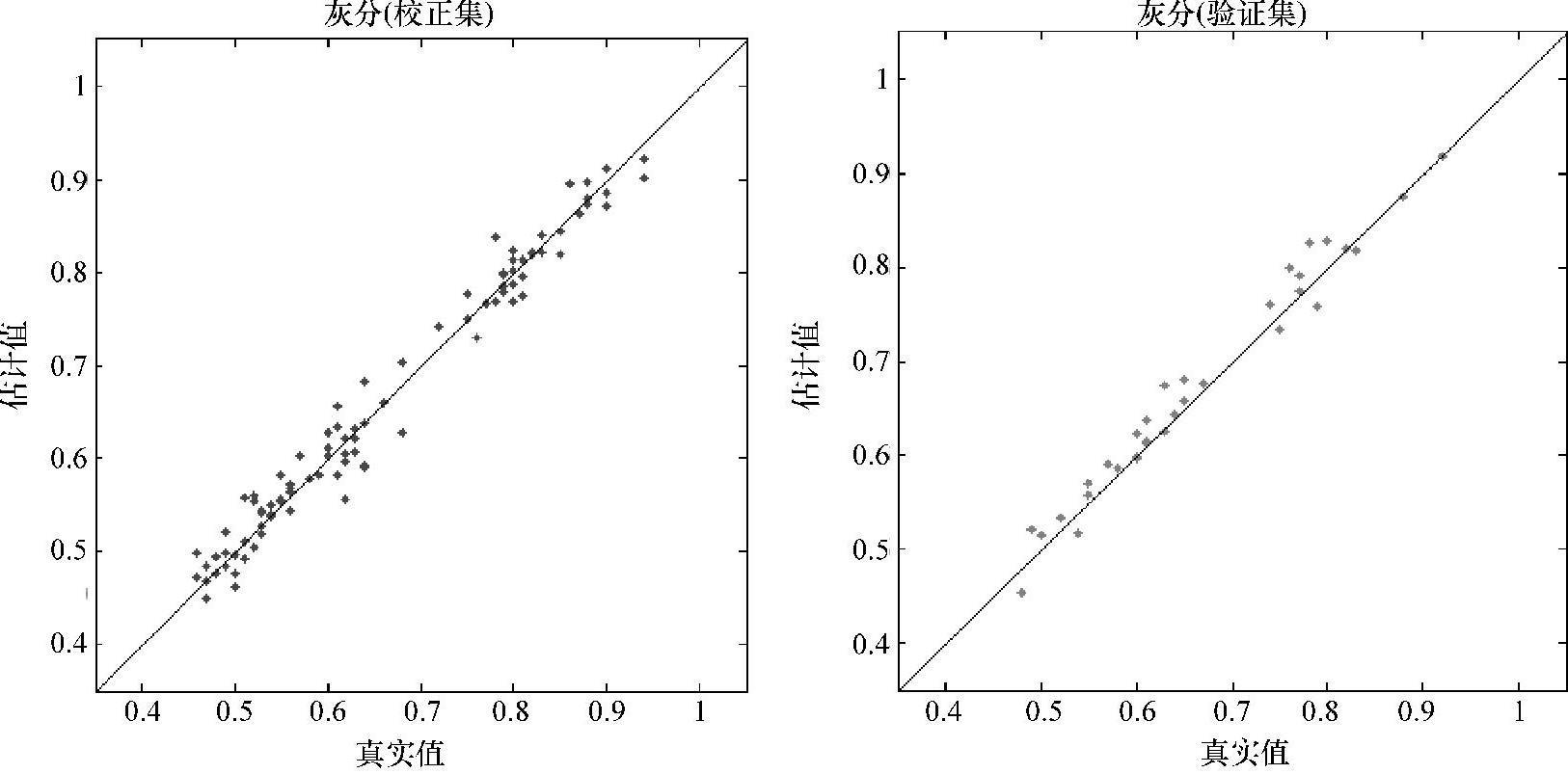
图10-11 Savitsky-Golay平滑（25）+GA的水分PLS定量模型

Savitsky-Golay平滑（25）结合遗传算法优化模型的检验集样本真实值与估计值误差见表10-8。

表10-8 检验集样本真实值与估计值误差

4.基于GA-PLS法的小麦粉湿面筋定量模型建立与分析

建立关于湿面筋含量的全谱PLS定量校正模型，并对检验集样本进行预测。模型预测结果如图10-12所示。

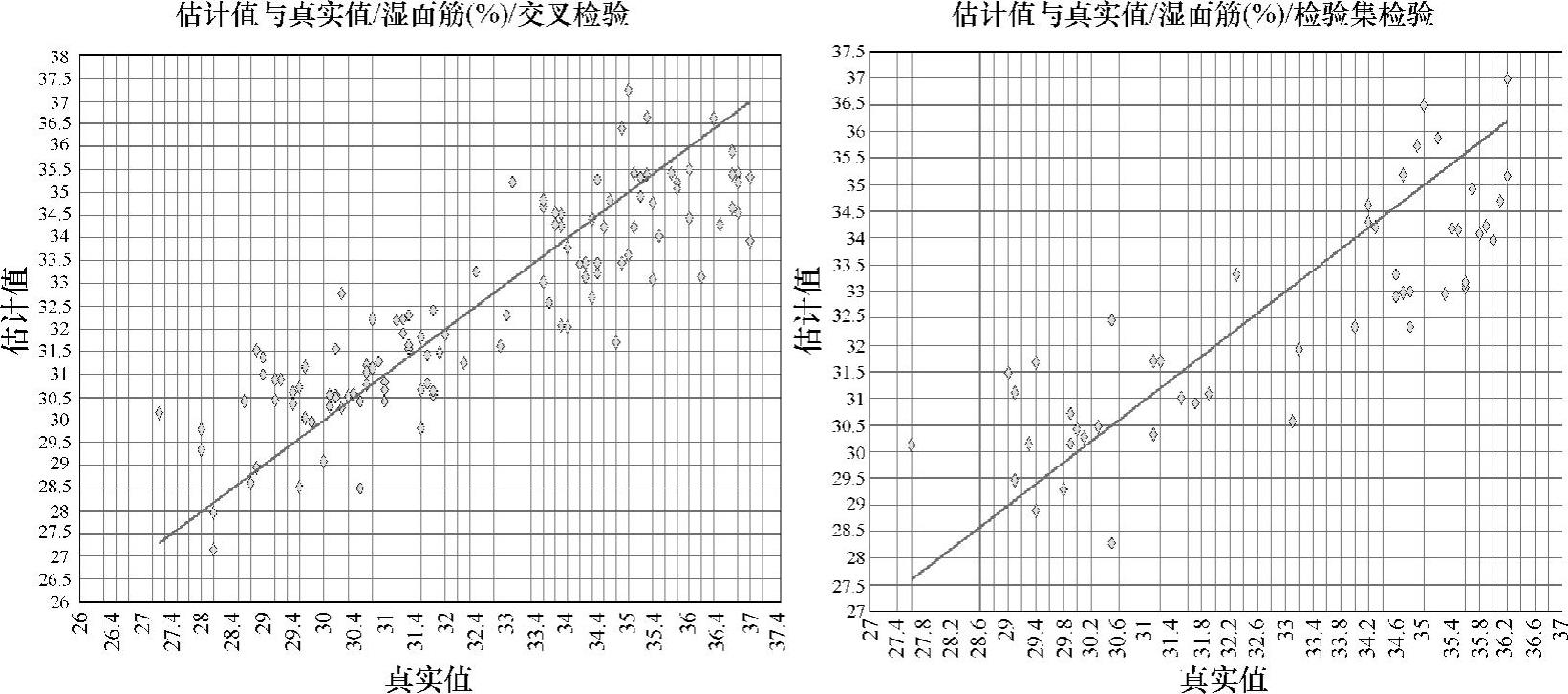
图10-12 湿面筋全谱PLS定量模型

湿面筋含量的全谱PLS定量模型相关系数R²为76.37，RMSECV为1.27，RESEP为1.45，RPD为2.53，RMSEP/RMSECV为1.058。

实验在建立基于遗传算法优化波长的小麦粉中灰分含量PLS定量模型时，种群规模设定为30，最大迭代次数设定为150，提取特征波长数量为80，适应度函数选择RMSEP。

特征波长数量随模型相关系数R²和RMSEC的变化如图10-13所示，算法在特征波长数量为80时趋于平稳。

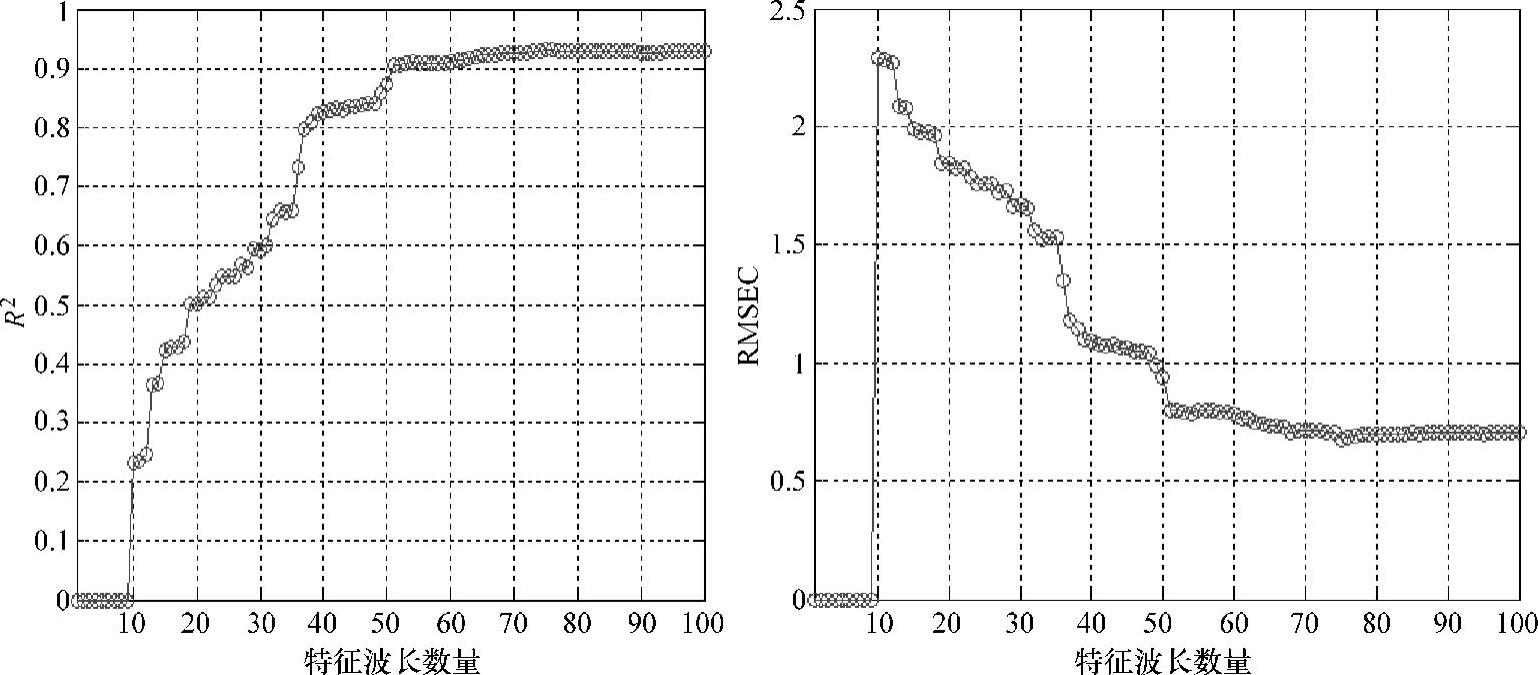
图10-13 特征波长数量随模型相关系数R²和RMSEC的变化

将湿面筋全谱PLS定量模型采用各光谱预处理方法以及遗传算法优化模型，各方法优化结果见表10-9。

表10-9 光谱预处理结合遗传算法优化模型结果（湿面筋）

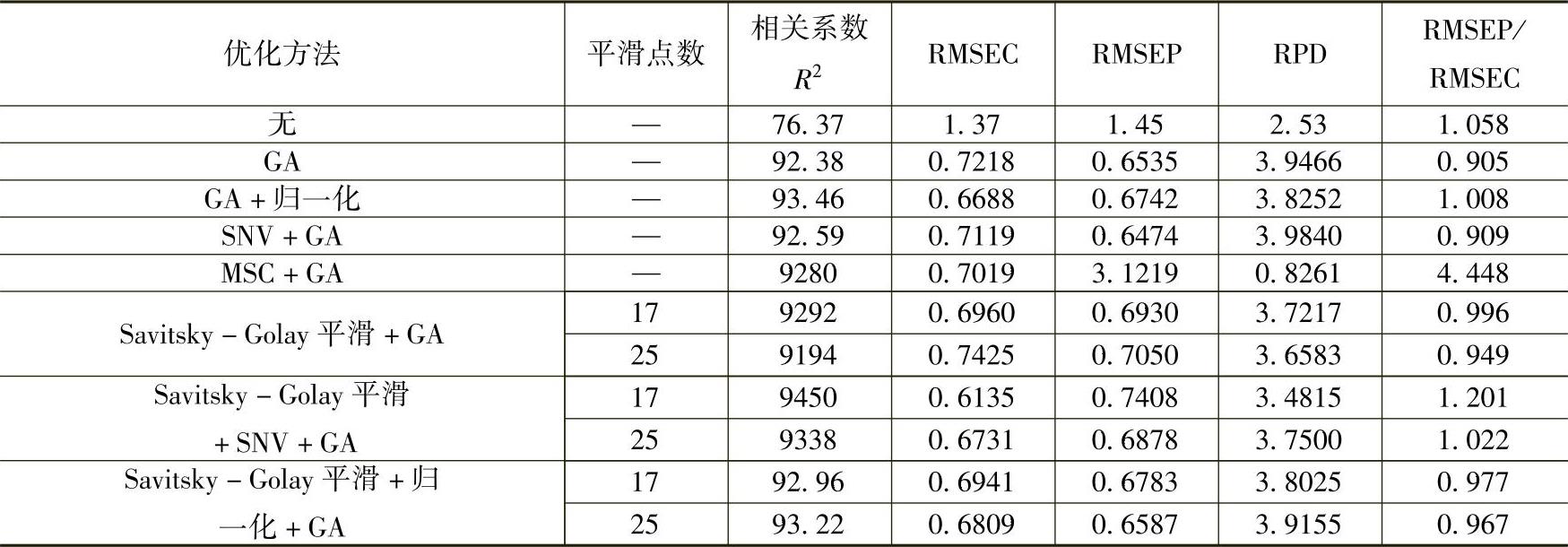
从实验结果看，模型经遗传算法筛选特征波长后，预测准确度有了大幅提高，并且结合适合的光谱预处理方法后，模型得到了更完善的优化。根据模型的准确度与稳健性参数，Savitsky-Golay平滑（25）点+归一化结合遗传算法优化模型结果较好，相关系数R²为93.22，RMSEC为0.6809，RMSEP为0.6587，RPD为3.9155。但模型预测准确度还需提高。

光谱经Savitsky-Golay平滑（25）+归一化预处理后光谱图如图10-14所示。

Savitsky-Golay平滑（25）+归一化结合遗传算法优化的灰分PLS定量分析模型如图10-15所示。

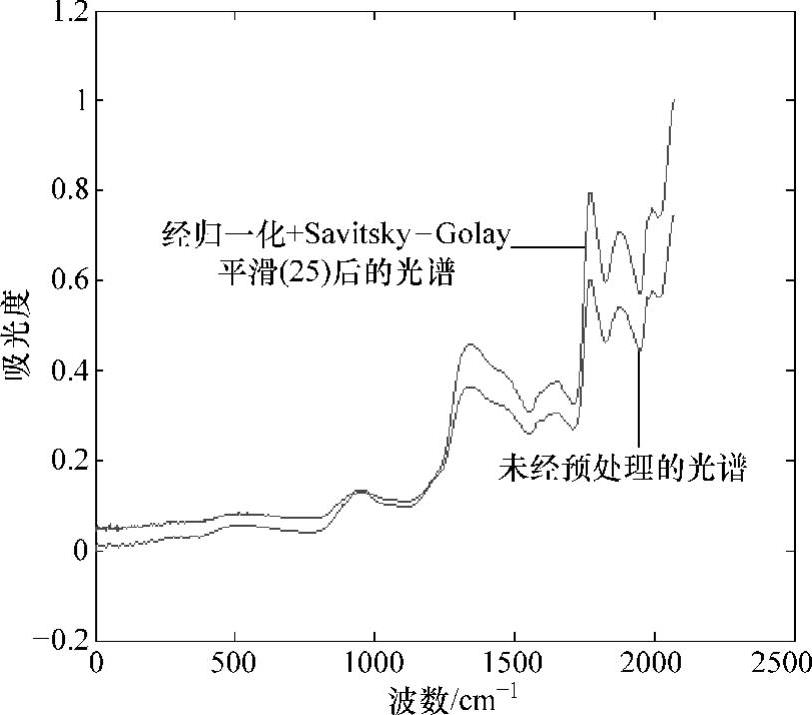
图10-14 Savitsky-Golay平滑（25）+归一化预处理后的光谱图

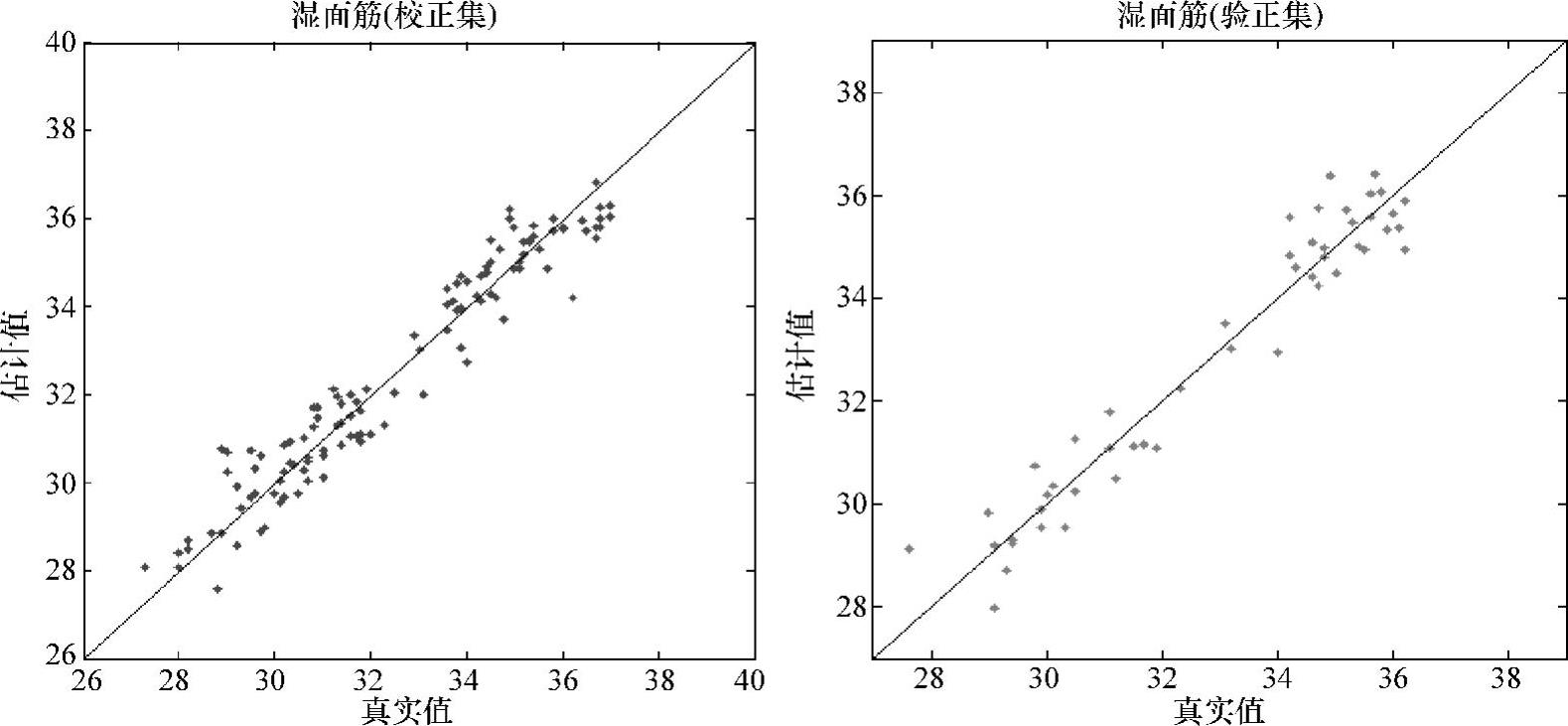
图10-15 Savitsky-Golay平滑（25）+归一化结合GA的水分PLS定量模型

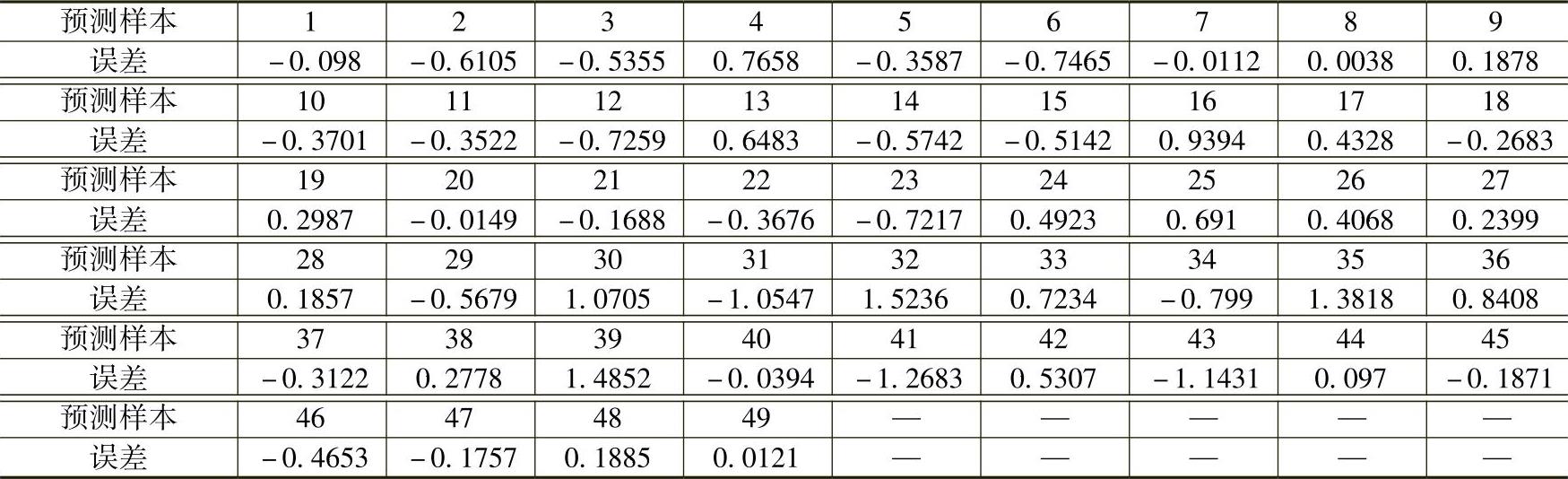
Savitsky-Golay平滑（25）+归一化结合遗传算法优化模型的检验集样本真实值与估计值误差见表10-10。

表10-10 检验集样本真实值与估计值误差