使用Savitzky-Golay卷积平滑法降噪

由光谱仪得到的光谱信号中既含有有用信息，同时也叠加着随机误差，即噪声。信号平滑是消除噪声最常用的一种方法，其基本假设是光谱含有的噪声为零均值随机白噪声，若多次测量取平均值可降低噪声提高信噪比。常用的信号平滑方法有移动平均平滑法和Savitzky-Golay卷积平滑法。

1.移动平均平滑法

如图2-6所示，移动平均平滑法选择一个具有一定宽度的平滑窗口（2ω+1），每个窗口内有奇数个波长点，用窗口内中心波长点k以及前后ω点处测量值的平均值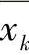代替波长点的测量值，自左至右依次移动k，完成对所有点的平滑：

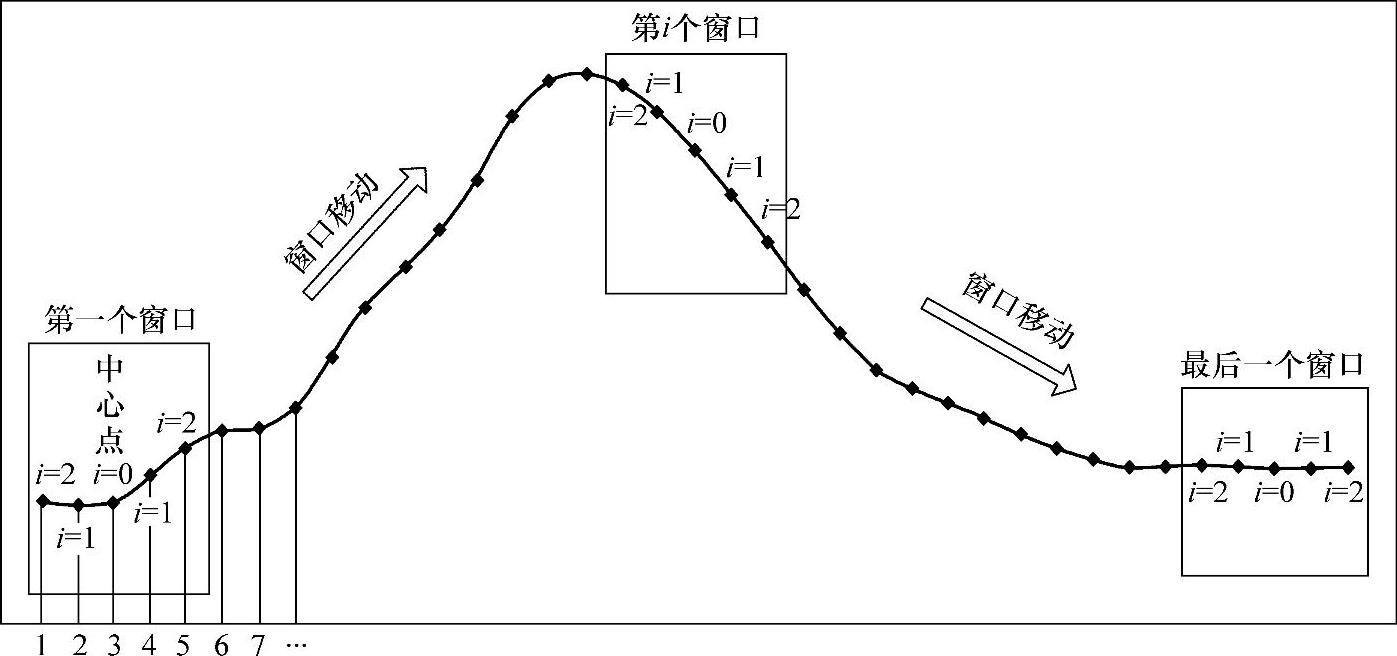
图2-6 窗口移动平滑法示意图

采用移动平均平滑法时，平滑窗口宽度是一个重要参数，若窗口宽度太小，平滑去噪效果将不佳，若窗口宽度太大，进行简单求均值运算，会在对噪声进行平滑的同时也将有用信息平滑掉，造成光谱信号的失真，如图2-7所示。

2.Savitzky-Golay卷积平滑法(www.xing528.com)

Savitzky-Golay（S-G）卷积平滑又称多项式平滑，波长k处经平滑后的平均值为

式中，h_i为平滑系数；H为归一化因子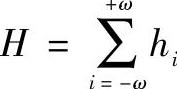，，每一测量值乘以平滑系数h_i的目的是尽可能减小平滑对有用信息的影响。

Savitzky-Golay卷积平滑法与移动平均平滑法的基本思想是类似的，只是该方法没有使用简单的平均而是通过多项式来对移动窗口内的数据进行多项式最小二乘拟合，其实质是一种加权平均法，更强调中心点的中心作用。Savitzky-Golay卷积平滑法是目前应用较广泛的去噪方法，移动窗口宽度（常称平滑点数）的影响要明显低于移动平均平滑法。

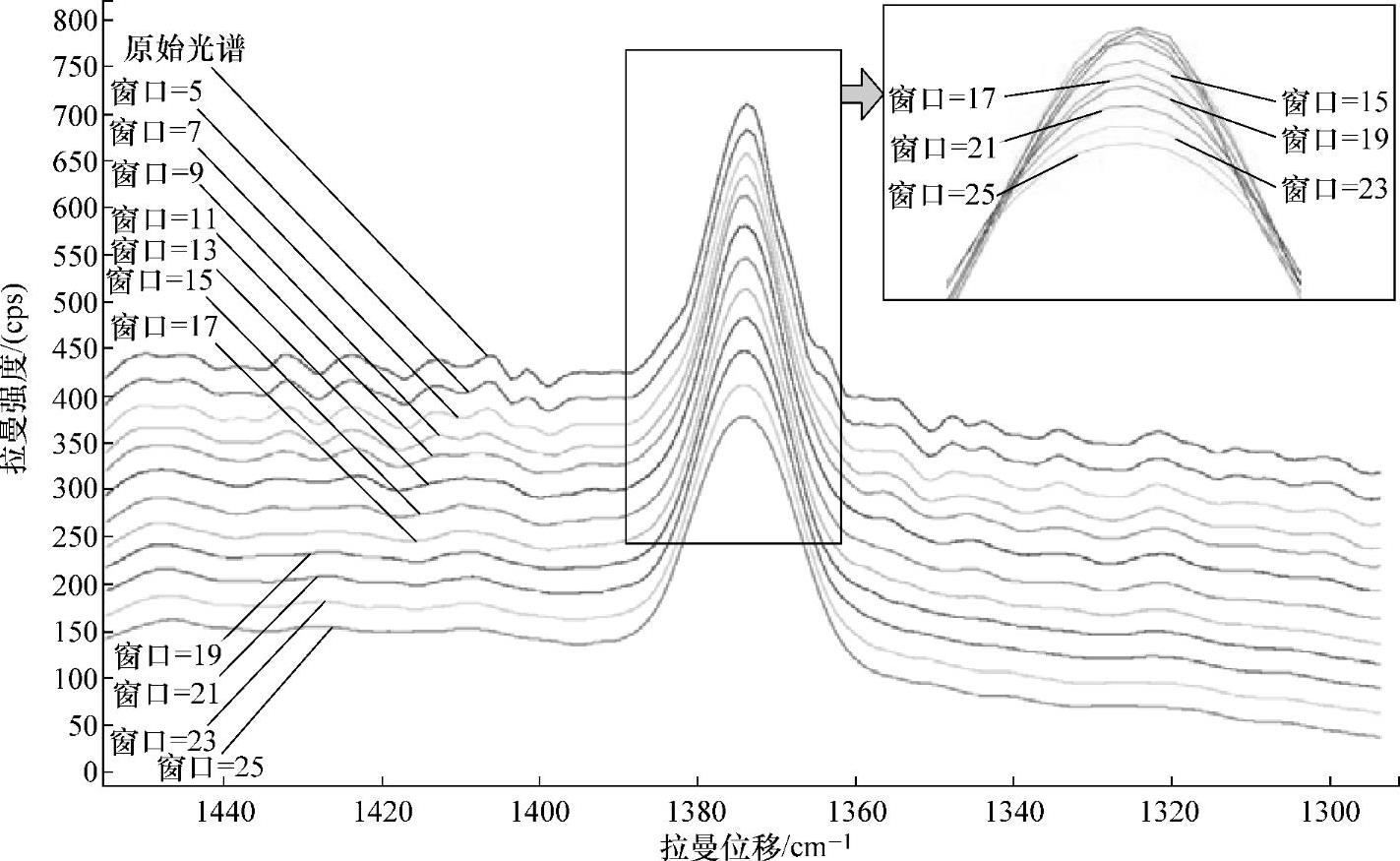
图2-7 不同窗口宽度对平滑效果的影响