焊接机器人运动探究

机器人的运动设计时，对机器人（机械手）末端执行器相对于固定参考坐标系的空间几何描述（即机器人的运动学问题）是机器人动力学分析和轨迹控制等相关研究的基础。机器人运动学即是研究机器人手臂末端执行器位置和姿态与关节变量空间之间的关系。

通常对机器人的位置和姿态描述方式有三种：① 机器人一端固定，另一端是用于安装末端执行器（如手爪）的自由端；② 机器人由 N 个转动或移动关节串联而成一个开环空间尺寸链；③ 机器人各关节坐标系之间的关系可用齐次变换来描述。

1.齐次坐标

一般来说，n 维空间的齐次坐标表示是一个（n＋1）维空间实体。有一个特定的投影附加于n维空间，也可以把它看作一个附加于每个矢量的特定坐标-比例系数。

如图 6.4 所示，空间任意一点 P 的位置可表示为：① 矩阵表示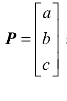；③ 矢量的模；② 矢量和表示，单位矢量|P|=1。

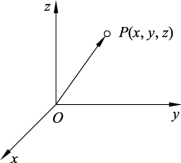
图6.4　空间一点P的位置表示

式中，w为比例系数。

通常齐次坐标表达并不是唯一的，随 w 值的不同而不同。在计算机图型学中，w 作为通用比例因子，它可取任意正值，但在机器人的运动分析中，总是取w=1。

2.刚体自由度

物体能够相对坐标系进行独立运动的数目称为自由度。如图6.5所示，刚体的自由度数目：

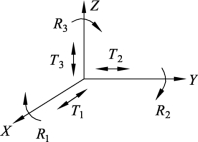
图6.5　刚体的自由度数目

（1）三个平移自由度T1、T2、T3。

（2）三个旋转自由度R1、R2、R3。

利用固定于物体的坐标系描述方位（Orientation）。方位又称为姿态（Pose）。相对于参考坐标系{A}，坐标系{B}的原点位置和坐标轴的方位可以由位置矢量和旋转矩阵描述。刚体B在参考坐标系{A}中的位置利用坐标系{B}描述。(www.xing528.com)

3.齐次变换

齐次变换是在齐次坐标描述基础上的一种矩阵运算方法，齐次变换使齐次坐标做移动、旋转等几何变换。通常将运动变换分为平移坐标变换、旋转坐标变换、复合变换三类。

（1）平移坐标变换：如图 6.6 所示，在坐标系{B}中的位置矢量BP在坐标系{A}中的表示可由矢量相加获得，即

（2）旋转坐标变换：如图 6.7 所示，坐标系{B}与坐标系{A}原点相同，则P点在两个坐标系中的描述具有下列关系：

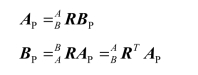
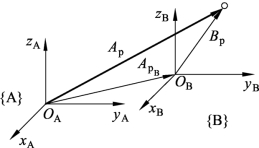
图6.6　平移坐标变换

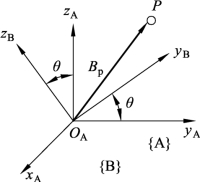
图6.7　旋转坐标变换

分别绕x、y、z 轴的旋转变换（基本旋转变换）：任何旋转变换可以由有限个基本旋转变换合成得到，即

（3）复合变换，如图6.8所示，就是通过平移和旋转构成的组合变换。即

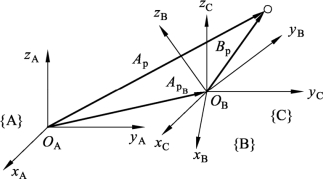
图6.8　复合变换