多尺度法：提高计算精度的有效方法

前面叙述的平均法是利用两种不同的时间尺度，将系统的振动分解为快变和慢变两种过程。将标志运动的主要参数，如振幅和初相角，在快变过程的每个周期内平均化，然后着重讨论其慢变过程。为了提高平均法的计算精度，可以将时间尺度划分得更为精细，由此发展为20世纪60年代的多尺度法（Multiple Scale Method）。与摄动法相比，多尺度法的明显优点是不仅能计算周期运动，而且能计算耗散系统的衰减振动；不仅能计算稳态响应，而且能计算非稳态过程；也可以分析稳态响应的稳定性，描绘非自治系统的全局运动性态。

为说明振动过程中不同时间尺度的存在，以林滋泰德—庞加莱法的级数展开式（6-35）为例，可以看出，用式（6-35）表达的振动过程包含不同的时间尺度t，εt，ε2t…的时间历程。不同的时间尺度描述变化过程的不同节奏，阶数越低，变化越缓慢，阶数越高，变化越迅速。对于精确到εm阶的解，将依赖于t，εt，ε2t…，εm-1t。

引入表示不同尺度的时间变量

则非线性振动过程为不同尺度时间变量的函数，可写为

其中m 为小参数的最高阶次，取决于计算的精度要求。将不同尺度的时间变量视为独立变量，则x（t，ε）成为m 个独立时间变量的函数，对时间的微分可利用复合函数微分公式按ε的幂次展开

其中Dn为偏微分算子符号

将式（6-59）、式（6-60）和式（6-58）代入方程（6-29）并展开，比较ε的系数，得到线性的偏微分方程组，依次求解，附加不出现久期项的初始条件，就可以得到式（6-58）中各个未知函数xi的确定表达式。

【例8】用多尺度法求方程的二阶近似解。

【解】设二阶近似解

将上式及式（6-60）代入方程得

展开后，令ε的同次幂系数为零，得到各阶近似的线性偏微分方程组

将式（6-64）中零次近似方程的解写为复数形式

其中A 为待定的复函数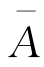，为A 的共轭复数。将式（6-65）代入一次近似方程（6-64）第二式的右边，得到

式中cc表示其左边各项的共轭复数。为避免久期项出现，函数A 必须满足

则从方程式（6-66）解出(www.xing528.com)

其中式（6-68）的振幅A 随时间T1的慢变规律由微分方程（6-67）确定。

将式（6-65）和式（6-68）代入二次近似方程（6-64）第三式的右边，得到

为消除久期项，要求

从方程式（6-69）解出

微分方程式（6-70）确定振幅A 随T2的变化规律。

将复函数A 对t的导数写为

其中D0A=0，D1A、D2A 分别由条件式（6-67）和式（6-68）确定，导出A 应满足的常微分方程

将复函数A 写为指数形式

其中a（t）和θ（t）皆为t的实函数。代入方程式（6-73），将实部与虚部分开，得到a 和θ的一阶常微分方程组

积分此二方程，得到

其中积分常数a0、θ0取决于初始条件。代入式（6-74）得到

将上式代入式（6-65），式（6-68）和式（6-71），最终得到方程的二阶近似解

其中