平均法：一种非线性振动解析方法

前面叙述的几种近似解析方法，对于弱非线性系统原则上可求出满足任意精度要求的周期解。但在具体计算时，ε的次数越高，计算工作越烦琐。如果所要求的精度只限于ε的一次项，则可采用更为有效的方法直接求出次近似解，这就是非线性振动解析方法的次近似理论，其中最主要的方法为平均法（Average Method）。

弱非线性系统的自由振动式（6-29）的派生系统式（6-30）的自由振动解为

其中任意常数a 和θ取决于初始条件。

应用常数变易法，把a 和θ看作t的函数，以此作为方程式（6-29）的解，对式（6-48）求导得

令

则

对式（6-51）求导得

将式（6-48）、式（6-51）、式（6-52）代入方程（6-29）得

从式（6-50）和式（6-53）得出a 和θ的微分方程

如果上式能求精确解，代入式（6-48）可得原方程（6-29）的解，不过这种情况是极少的。现在用一种特殊方法求方程式（6-54）的近似解。当参数ε充分小时，a 和θ是在常数附近缓慢变化的函数，它们在一个周期内的改变量为(www.xing528.com)

将式（6-54）代入上式得

再用近似值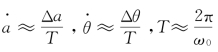，得

以上两个方程中，右端都仅仅是a 的函数，积分可得到a（t）和θ（t），在积分过程中，积分常数可根据初始条件a（0）=a0，θ（0）=θ0确定。

简化的方程式（6-56）可以看作是方程式（6-54）在一个周期内取平均值得到，故称为平均法。

【例7】用平均法求方程的近似解。

【解】这里，代入方程式（6-56）得

积分得

近似解为