奇点的基本类型解析

6.2.3.1 轨线在平衡点附近的分布情况

对于非线性系统，设在奇点x=0，y=0的某一区域内可解，即P（0，0）=0，Q（0，0）=0。

将函数P 和Q 按泰勒级数展开，可得

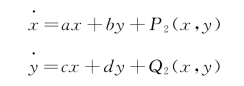
式中

根据常微分方程定性理论，令

p=a+d，q=ad-bc，Δ=p2-4q

当p≠0，q≠0，Δ ≠0时，式（6-5）与其线性化系统

在原点附近的积分曲线的几何拓扑结构相同。

现研究式（6-9）的非平凡解，设

式中：r，s，λ为待定常数，均可为复数，现将式（6-10）代入式（6-9），可得

式（6-11）有非平凡解（即r，s，λ皆不为零），可存在以下特征

展开后，有

若设p=a+d，q=ad-bc，则上式可改写为

λ2-pλ+q=0

其根为

λ称为特征根，其可能是实根也可能是复根。

实根存在以下三种情况：

（1）λ1＞0，λ2＞0或λ1＜0，λ2＜0（同号）；

（2）λ1＜0，λ2＞0（异号）；

（3）λ1=λ2。

复根存在以下两种情况：

（1）若p ＞0或p＜0，设Δ=p2-4q＜0，q＞0，则有共轭复根；

（2）若p=0，Δ=p2-4q＜0，q＞0，则有纯虚根。

以p，q为直角坐标，在p-q平面上（见图6-3），直线q=0，半直线p=0，q＞0与抛物线Δ=0将平面划分为5个区域Ⅰ～Ⅴ，可描述以上五种根的分布情况。

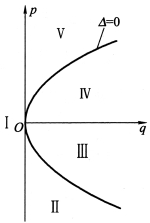
图6-3

对于系统式（6-9）的通解，由区域Ⅰ～Ⅴ的情况，Δ ≠0，故λ1≠λ2，矩阵A 的Jordan标准形式为

可得出其通解为

式中：C1，C2为任意常数，r1，s1为λ=λ1时由式（6-11）所确定的r，s的固定值，r2，s2为λ=λ2时由式（6-11）所得的r，s的固定值。

由此可得

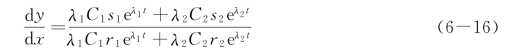
现分别对区域Ⅰ～Ⅴ内的奇点、相轨线及稳定性进行探讨。

（1）区域Ⅰ（q＜0）。

当q＜0时，有Δ=p2-4q＞0，λ1，λ2均为实数，且λ1＞0，λ2＜0，由式（6-15）知，当C1=0时有解

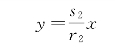
当C2=0时有解

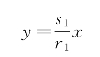
从以上两式可见，通过奇点的积分曲线是两条直线L1，L2，如图6-4所示。其相点的运动，当t→+∞时，由C1=0的解可知，相点的运动趋于奇点O；当t→-∞时，由C2=0的解可知，相点的运动趋于奇点O。由式（6-16）可知：在一般情况下，C1，C2均不为0，当t→+∞时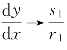，而当t→-∞时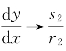，，相平面图如图6-4所示为双曲线。L1，L2直线为其他解的渐近线，称为分界线。系统的奇点称鞍点，鞍点显然是不稳定的。

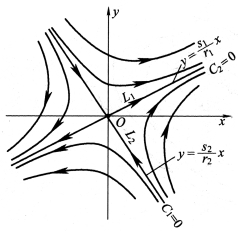
图6-4

（2）区域Ⅱ（q＞0，p＜0，Δ ＞0）。

在此区域中λ1，λ2均为实数，且λ2＜λ1＜0，现将式（6-16）写为

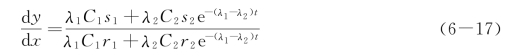
当C1=0时解沿直线L2，为

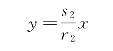
当t→+∞时，相点的运动趋于奇点O，当C2=0时解沿直线L1，为

此情况与（1）不同，见图6-5。

当C1，C2均不为0，则当t→+∞时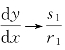，。由此可见，所有的解除直线L2外，均与直线L1在奇点相切（当t→+∞），而其另一端则与直线L2平行，即二者斜率相等（当t→-∞）。

此时系统的奇点称为节点，从图6-5可见，节点显然是稳定的。，而当t→-∞时，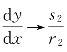

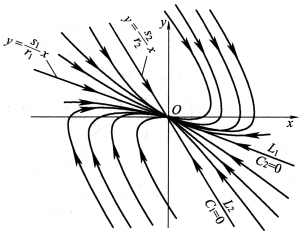
图6-5

（3）区域Ⅲ（q＞0，p＜0，Δ ＜0）。

在此区域中λ1，λ2为共轭复根，并有负实部。

式中

此时式（6-15）可改写为

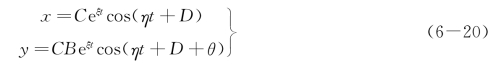
式中C，D 为任意常数，B，θ有固定值。

引入标准形式的矩阵A

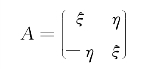
通过线性变换，把方程式（6-9）变为

进一步再将上式转换为极坐标形式

u=r cosφ，v=r sinφ

可得

积分得

当t→+∞时，r→0。u-v平面上的相图如图6-6（a）所示，为一族围绕奇点O 的螺线，当t→+∞时，相图趋向于奇点O。转回x-y 平面，则其相平面图如图6-6（b）所示。(www.xing528.com)

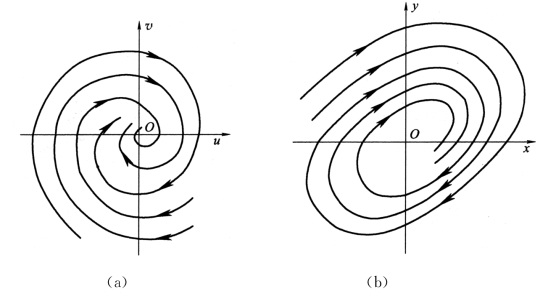
图6-6

此时系统的奇点称为焦点，从图6-6中可见，焦点显然是稳定的。

（4）区域Ⅳ（q＞0，p＞0，Δ ＜0）。

同区域Ⅲ一样，λ1，λ2也为共轭复数，但有正实部，即ξ＞0。由式（6-23）可知，系统在u-v平面上的相平面如图6-7所示，为一族围绕奇点O 的螺线，当t→-∞时，r→0，系统的奇点O 为不稳定焦点。

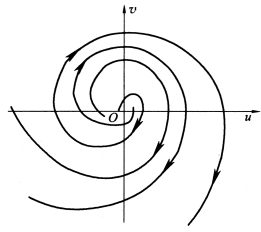
图6-7

（5）区域Ⅴ（q＞0，p＞0，Δ ＞0）。

同区域Ⅱ一样，此时λ1，λ2均为实数，但λ1＞λ2＞0。由式（6-15）知：当t→-∞时，x→0，y→0相轨线趋于奇点，当C1=0时，有解；当C2=0时，有解。再由式（6-17）知：C1，C2均不为0，则当t→-∞时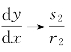，，当t→+∞时，。系统的相平面如图6-8所示，奇点O 为不稳定节点。

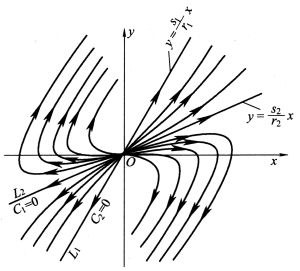
图6-8

根据以上分析可得如下结论：

（1）当λ1，λ2为负或都有负实部时，所有的相轨线都趋于奇点O，这种奇点称为汇，且是稳定的，又是渐进稳定的；

（2）当λ1，λ2都为正或都有正实部时，所有的相轨线都远离奇点O，即当t→-∞时，相点的运动趋于奇点O，这种奇点称为源，且是不稳定的。

6.2.3.2 区域边界线上的奇点

图6-2中五个区域之间有五条边界线，边界线上奇点的分析，可同样应用以上的方法进行。在此只给出如下结论。

（1）区域Ⅲ、Ⅳ间的边界线（q＞0，p=0）。

根据式（6-23）知，此时，相轨线为一族同心圆，圆心在原点，如图6-9（a）所示。根据式（6-20）知，在相平面x-y 上的相轨线为中心在原点的一族椭圆，如图6-9（b）所示，相当于的情况。

系统的奇点称为中心，中心显然是稳定的，但不是渐进稳定的。

（2）区域Ⅱ、Ⅲ间的边界线（q＞0，p＜0，Δ=0）。

此时，特征方程有等根λ1=λ2=λ=0，矩阵A 的Jordan标准形式有两种情况。

①Jordan标准形式为对角矩阵。

在这种情况下，在相平面u-v 上的相轨线为一族半直线［见图6-9（c）］，其奇点O 称为星形节点，或临界节点，节点是稳定的，又是渐进稳定的。

②Jordan标准形式不是对角矩阵，即化为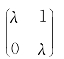

在此种情况下，相平面x-y 上的相轨线相当于图6-5中L1与L2两直线重合。这种奇点称为一轴节点，节点是稳定的且是渐进稳定的。与此相对照，图6-5中的节点也称为二轴节点。

（3）区域Ⅳ、Ⅴ间的边界线（q＞0，p＞0，Δ=0）。

由以上分析可知，若Jordan标准形式为对角矩阵，则相平面u-v上的相轨线如图6-9（c）所示；若Jordan标准形式不为对角矩阵，则相平面u-v 上的相轨线如图6-9（d）所示。在这种情况下，相平面x-y 上的相轨线相当于图6-8中L1和L2两直线重合。

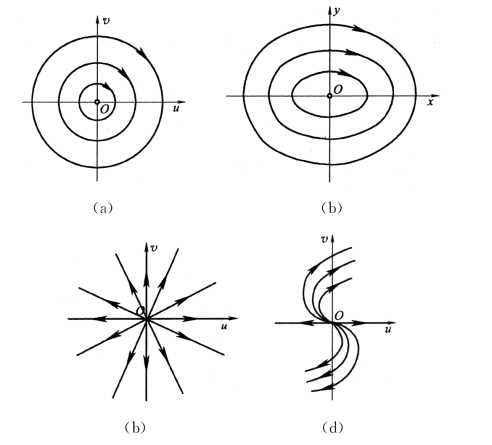
图6-9

奇点O 在上述两种情况下，分别为不稳定星形节点与不稳定一轴节点。

（4）区域Ⅰ、Ⅱ间的边界线（q=0，p＜0）和区域Ⅰ、Ⅴ间的边界线（q=0，p＞0）。

系统（6-9）的奇点不是孤立的，沿直线ax+by=0（或cx+dy=0）上的点都是奇点。

纵观以上分析结果，可获得p-q平面内系统（6-9）的奇点分类如图6-10所示。奇点的基本类型为鞍点、节点、焦点和中心共四种。

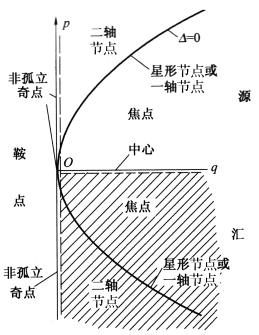
图6-10

【例2】求系统（式中ε＞0）的奇点及其类型，并画出奇点附近的相图。

【解】根据式（6-4），有

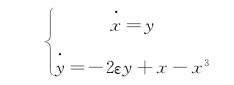
由式（6-7）可知

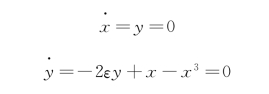
可求出奇点

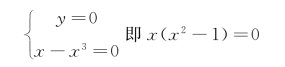
故可得三个奇点为（0，0）、（-1，0）、（1，0）。

现判别奇点的类型。

①讨论奇点（0，0）附近的情况。

由式（6-9）

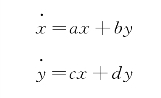
知系统的线性化方程是

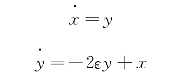
可得

a=0，b=1，c=1，1d=-2ε

根据p=a+d=-2ε＜0，q=ad-bc=-1＜0，由图6-9可知奇点（0，0）为不稳定的鞍点。

②讨论奇点（-1，0）附近的情况。

现令x=ξ-1，y=η，得

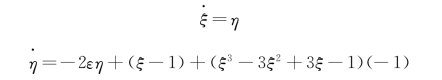
则线性化方程为

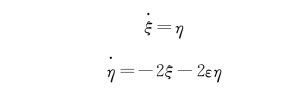
可得

a=0，b=1，c=-2，d=-2ε

根据

p=a+d=-2ε＜0，q=ad-bc=2＞0

则得到如下结论。

（a）当时，Δ ＞0，则由图6-9知奇点（-1，0）为稳定的，且为二轴节点。

（b）当时，Δ=0，根据判断Jordan的标准形式为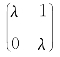，故奇点为稳定的一轴节点。

（c）当时，Δ ＜0，奇点（-1，0）为稳定的焦点。

③讨论奇点（1，0）附近的情况。

令x=ξ+1，y=η得

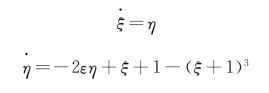
则线性化方程为

可得

a=0，b=1，c=-2，d=-2ε

其结论与上述②结论相同。

当时，奇点（1，0）为稳定的二轴节点。

当时，奇点（1，0）为稳定的一轴节点。

当时，奇点（1，0）为稳定的焦点。

综合以上分析，可画出奇点的相图如图6-11所示。

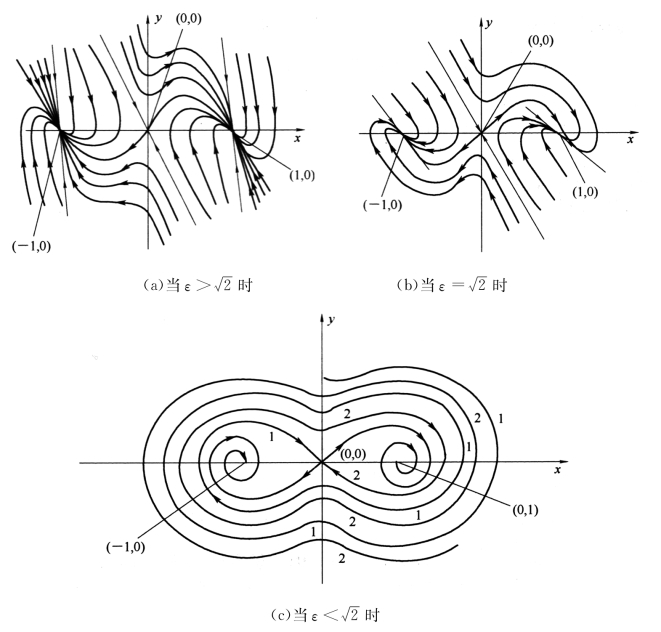
图6-11