常点和奇点：积分曲线与相轨线的交叉情况

6.2.2.1 定义

一般情况下，单自由度自治系统的振动方程可表示为

其中P（x，y）和Q（x，y）在整个Oxy 平面上是解析函数。

若x-y 平面上一点（x0，y0）满足

则称（x0，y0）为方程式（6-5）的常点。若此点使

则称（x0，y0）为方程式（6-5）的奇点。

6.2.2.2 积分曲线、相轨线

1.积分曲线

从数学观点出发，式（6-5）的解只有在常点处才符合微分方程解的存在、唯一性的条件。现将式（6-5）中的两式相除，得

上述方程在奇点处没有确定的切线方向（因为方程的右边不连续）。

2.相轨线

从单自由度自治系统的振动方程的观点出发，式（6-5）的解不仅含有常点，还含有奇点。

根据式（6-2）可知，若奇点处y（即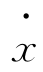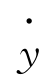速度）、（即加速度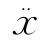）同时为零，则奇点对应于系统的平衡状态。对式（6-5）而言，奇点则定义为系统的平衡点。从力学意义来理解时，奇点对应于系统的静止状态，常点则对应于系统的运动状态，即在奇点处，式（6-8）的积分曲线可以有不同的切线或者退化为孤立点。

3.积分曲线与相轨线的区别

积分曲线上每一点的斜率按公式（6-8）确定，只含有常点。(www.xing528.com)

相轨线的运动规律由式（6-5）确定。其常点处的相迹和积分曲线重合，奇点可按式（6-7）确定。

【例1】求系统的相平面图。

【解】由式（6-8）得

对上式积分得

x2+y2=C

获得的积分曲线为一族同心圆（见图6-2），也是常点的相轨迹。

由式（6-7）可求出奇点。由

P（x，y）=0 xy=0

Q（x，y）=0 x2=0

得到奇点为

y ≠0，x=0

x=0，y=0

即在y 轴上的各点也是相轨迹。

考虑到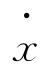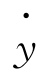，在各象限的正负，相轨迹上的箭头上如图6-2所示。

根据图6-2可知：①每一积分曲线都通过奇点；②每一个通过奇点的积分曲线都是由三条相轨线组成的，例如通过奇点A 时，其一A 为平衡点，另两条相轨线在t→-∞时渐进地趋向A 点；同样通过奇点B 的积分曲线也是由三条相轨线组成的，其中两条轨线在t→+∞时渐进地趋向平衡点B（注意：奇点也相当于一“条”相轨线）。

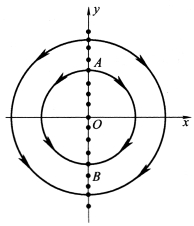
图6-2

由此可见，积分曲线只有一条，但通过奇点的相轨线不是一条而是三条。